注意力评分函数 笔记

10.3. 注意力评分函数 — 动手学深度学习 2.0.0 documentation

有错请指正

1.键是key 查询是query

用a函数算出key与query的注意力评分(类似于距离,距离太远注意力应该少点,近的应该放近一点),

得到评分之后,根据评分softmax归一化让每一个query的评分变小,让数据变小.同时得到在整体query的占比,也变成了注意力权重

2.使用注意力权重,乘以所有的值value,和求和后得到非求和平均的函数拟合值,输出出去

3.拟合值表现为注意力重点放在权重高的地方,而不再是所有地方全都加起来平均.

4.拟合值全求出来之后连线就是拟合出来的f(x) 函数

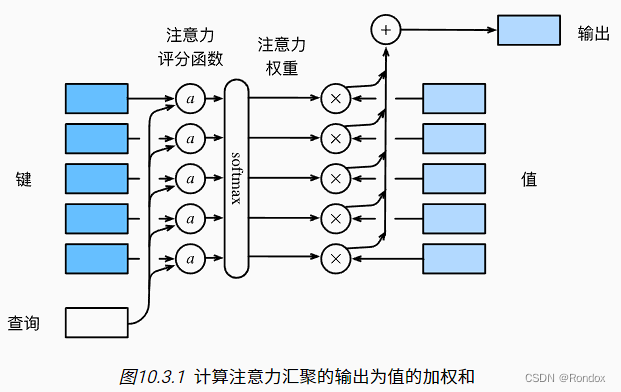
5.而此处a函数 也就是注意力评分函数是可以变的,也就是说根据不同的算法算出不同的结果,上一节是核回归变换出来一个算法 就是红框的那个

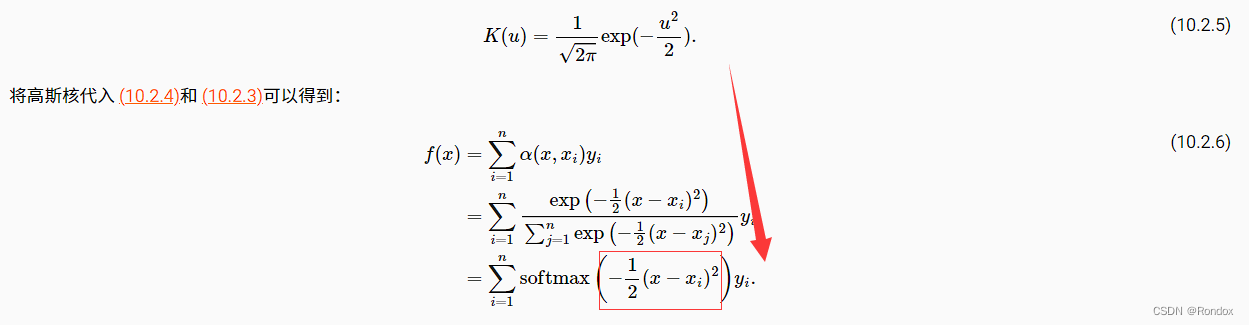
 这是非参数的算法

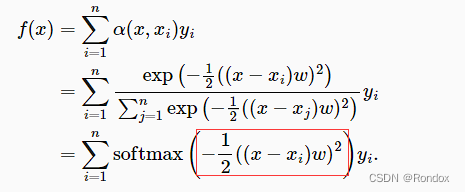
这是参数算法

6.这是我们学习到第一种通过加入参数让函数更加拟合真实函数, 

而我们可以换另一种函数,增多可以学习的参数让函数不那么的线性(对于w来说线性),增加多几个参数,拟合度就会更高

于是就变成了需要找到更好的注意力函数的身上 

7.这个过程个人感觉就是如果a函数是可以变的 参数是q和k,为了尽可能加多点参数,

q前面加个参数,w加个参数,而且q与k非线性,加起来也是非线性,这样就有了两个参数,这时候也不能直接在两者之和乘一个参数,如果这样的话乘法分配律可以乘进去,那第三个参数可以跟第一二个参数合并起来,所以需要别的手段

8.这个手段也就是激活函数,让这个和非线性化,使用tanh函数,然后这时候就可以再加一个参数了.同时加这个激活函数也可以让这个合归一化,使数值不要过大,于是就有了三个参数,这时候再加激活函数也可以被线性化 于是这时候是已经没办法加参数了 (纯属猜想,有错请指正)

9.查询和键是不同长度的矢量时,长度也不一样分别是q长和k长.

为了能相加,w_q和w_k的第一维必定和q和k,最后一维必定是一样的数,而w_q和w_k可以试试多维,此处使用了线性网络nn.Linear,最后一位是隐藏层hiddens

假设q和k都是一维 w_q*q+w_k*k就是hiddens*1 用w_v转置乘过去就能消掉hiddens的维数得到一个值  

但假如q和k多维那只会减少一维. 得到一个注意力分数

分析代码一:加性注意力 (处理q,k长度不同时候)

queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))

1.queries取正态分布(2, 1, 20)形状, batch_size为2,queries数为1(1个query放在里面),query的值长度为20

keys取全1的(2, 10, 2)形状 ,batch_size为2,键值对kv数为10(10对kv放在里面,并不是全部都有效,有些的padding的,后面会处理),key的值长度为2

可以看出q,k长度的确不一样

queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量，两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(
    2, 1, 1)
valid_lens = torch.tensor([2, 6])

2.长度不一样怎么相互运算或者说相互比较,取相似度呢. 这里使用参数W_q和W_k使得q的20长度的值的特征分散到hiddens长度的特征中去,k也一样,k的2长度的值的特征分散到hiddens长度的特征中去

各种的特征维度是一样的 所以就可以用于数据运算,数值比较.此处q*w_q+k*w_k加起来,以获取特征

q*w_q->(batch_size,q个数,hiddens层数)

k*w_k->(batch_size,kv对个数,hiddens层数)

单方面来想,首先我们一个q需要找出相似最高的kv对,这时候一个q->相似度最高的kv 1对1的关系,也就是形状(1,1),但是我们关注度集中放在最相似的kv,其他kv也要兼顾,只不过权重需要降低,所以要一个q->所有kv,也就是形状(1,kv对个数)

所以q与k结合后的形状可以预想出来是(batch_size,q个数,kv对个数,hiddens层数)

所以q*w_q在第3(下标2)维插入一个维度 对应kv对个数,所以k*w_k在第2(下标1)维插入一个维度,对应q个数

于是维度变化之后和在一起(batch_size,q个数,kv对个数,hiddens层数) 就是所有q各自对应所有kv对的权重分散到hiddens的特征,所以我们需要将hiddens层的特征集合起来,但是为了W_v可以训练和同时减少值的大小,使用激活函数tanh归一化(同时根据给出的valid_len删减张量长度),

最后删减和归一化后再通过乘W_v集合特征,性祖航变成了(batch_size,q个数,kv对个数,1),因为只有一个对象看起来.所以我们解除最后一个维度.变成(batch_size,q个数,kv对个数) 这时候就是真正的权重.

假设在第一个batch中,每个q对应的第一个kv为权重1,意义为每个q应该放多少注意力给第一个kv,代码就是weight[0,:,0]

又比如weight[0,0,0] 为第一个batch中第一个q对于第一个kv应该给多少注意力

3.在本节代码中我们将key的值是用ones生成的意味着所有的value的值都一样.所以我们无论输入什么样的q,q对于所有kv的相似度都是一样的.(比如q是1,所有kv都是10,q对所有kv都相似度都是一样的,比喻可能不太恰当),故权重平分有多少个kv就是1/kv个数的权重(因为归一化了,最大为1).

4.因为有valid_len的存在,也就是告诉你每个batch中,所有的kv中有几个是无效的,比如本代码的

valid_lens = torch.tensor([2, 6]),第一个batch只由2个kv有效,第二个batch只由6个kv有效,其余全是填充padding的.故在归一化之前就应该把无效的剔除掉.

归一化后那就是(batch_size,q个数,kv对个数)形状 (2,1,10)

[[0.5,0.5,...,0],

[0.16,0.16,0.16,0.16,0.16,0.16,0,0,0,0]] 

第一行表示第一个batch,第一个q 对应10个kv中,只由0,1两个下标的kv有效(不是padding的),同时kv的值都一样,相似度都一样,故权重应该平分,所以都是0.5

第一行表示第二个batch,第一个q 对应10个kv中,只由0到5的6个下标的kv有效(不是padding的),同时kv的值都一样,相似度都一样,故权重应该平分,所以都是0.16(其实应该是0.16666667 省略).

最后引出那个怎么看都看不懂的图

d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')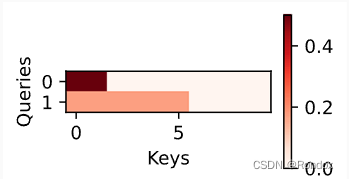

import math
import torch
from torch import nn
from d2l import torch as d2l

#@save
def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
                              value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)


masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))

masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))

#@save
class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播方式进行求和
        features = queries.unsqueeze(2) + keys.unsqueeze(1)#2,1,1,8  2,1, 10 ,8
        features = torch.tanh(features)
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数) #确实是有道理的 每个查询对应一个键的分数
        scores = self.w_v(features).squeeze(-1)
        self.attention_weights = masked_softmax(scores, valid_lens)#过滤掉不需要的key value pair
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)

#normal 怪不得看不懂
queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量，两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(
    2, 1, 1)
valid_lens = torch.tensor([2, 6])

attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,
                              dropout=0.1)
attention.eval()
attention(queries, keys, values, valid_lens)

d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')


#@save
class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)


queries = torch.normal(0, 1, (2, 1, 2))
attention = DotProductAttention(dropout=0.5)
attention.eval()
attention(queries, keys, values, valid_lens)

d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')

另外一种好像不分析都能看得懂就不写了