数据库系统（4）：关系模型之关系代数

最新推荐文章于 2024-09-26 18:01:24 发布

nowherebuthere

最新推荐文章于 2024-09-26 18:01:24 发布

阅读量1.4k

点赞数 5

CC 4.0 BY-SA版权

分类专栏：数据库

本文链接：https://blog.youkuaiyun.com/qq_36628619/article/details/88314167

本文详细介绍了关系代数的概念，包括并、差、积、选择、投影等基本操作，以及交、连接、除、外连接等扩展操作。关系代数是一种集合思维的操作语言，基于集合提供了一系列的关系代数操作，是学习数据库查询语言如SQL的基础。此外，文中还阐述了并相容性、外连接等关键概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

重点与难点

关系代数基本操作：并、差、积、选择、投影、（更名）

关系代数扩展操作：交、 $\theta$ -连接、自然连接

关系代数复杂扩展操作：除、外连接

书写关系代数的基本思维训练：“一个集合，施加一个操作得到一个集合，依次施加关系代数操作，进而得到所需结果” “以集合为中心”

一、什么是关系代数

关系代数运算的特点

基于集合提供了一系列的关系代数操作，是一种集合思维的操作语言

关系代数操作以一个或多个关系为输入，结果是一个新的关系

用对关系的运算来表达查询，需要指明所用操作，具有一定的过程性

是一种抽象的语言，是学习其他数据库语言，如SQL等的基础

关系代数操作：集合操作和纯关系操作

集合操作：并、交、差、笛卡尔积

纯关系操作：投影、选择、连接、除

二、并相容性的概念

参与运算的两个关系及其相关属性之间有一定的对应性、可比性或意义关联性

定义：关系R和关系S存在相容性，当且仅当：

关系R和关系S的属性数目必须相同

对于任意i，关系R的第i个属性的域必须和关系S的第i个属性的域相同

三、并（Union）操作

定义：假设关系R和关系S是并相容的，则关系R与关系S的并运算结果也是一个关系，记做： $R \cup S$ ，它由或者出现在关系R中，或者出现在S中的元组构成

数学表述： $R \cup S = \{t | t \in R \vee t \in S \}$ ，其中t是元组

并运算是将两个关系的元组合并成一个关系，在合并时去掉重复的元组

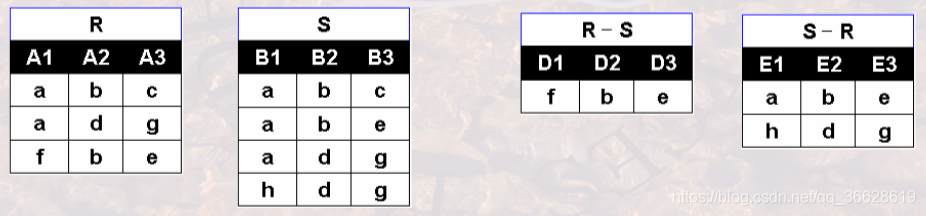
四、差（Difference）操作

定义：假设关系R和关系S是并相容的，则关系R与关系S的并运算结果也是一个关系，记做： $R - S$ ，它由出现在关系R中但不出现在S中的元组构成

数学表述： $R - S = \{t | t \in R \wedge t \notin S \}$ ，其中t是元组

五、广义笛卡尔积（Cartesian Product）操作

定义：关系R $(<a_{1},a_{2},...,a_{n} >)$ 与关系S $(<b_{1},b_{2},...,b_{m} >)$ 的广义笛卡尔积（简称广义积或笛卡尔积）运算结果也是一个关系，记做： $R \times S$ ，它由关系R中的元组与关系S的元组进行所有可能的凭借（或串接）构成。

数学描述：