08-图7 公路村村通（30 分）

最新推荐文章于 2023-09-07 16:03:55 发布

原创最新推荐文章于 2023-09-07 16:03:55 发布 · 988 阅读

0 ·

CC 4.0 BY-SA版权

陈越、何钦铭数据结构2018秋专栏收录该内容

16 篇文章

订阅专栏

本文介绍使用Prim算法解决修路成本最低的问题，通过构建最小生成树来找到连接所有节点的最短路径。代码详细展示了Prim算法的实现过程，包括初始化距离矩阵、寻找最小边、更新距离和父节点等关键步骤。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

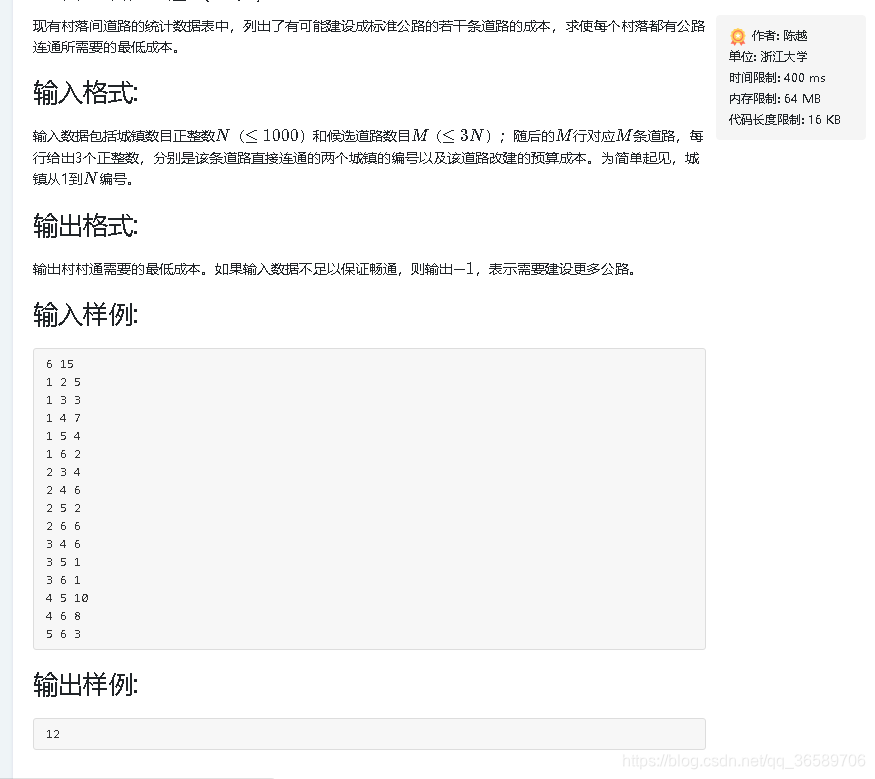
修路成本最低（贪心），用Prim算法（最小生成树）

比较Dijkstra算法和Prim算法

#include<cstdio>
#define INFINITY 65535
using namespace std;
const int maxn=1001;
int dist[maxn], C[maxn][maxn], parent[maxn];
int N, M, cnt;

int findMin(){
	int minn=INFINITY, index=-1;
	for(int i=1; i<=N; i++){
		if(dist[i]!=0&&minn>dist[i]){
			minn=dist[i];
			index=i;
		}
	}
	return index;
}
void Prim(int s){
	int cnt=1, Totalcost=0;
	for(int i=1; i<=N; i++){
		parent[i]=s; //记录父节点 （路径） 
		dist[i]=C[s][i];
	}
	parent[s]=-1;
	dist[s]=0;
	int v;
	while(1){
		v=findMin();
		if(v==-1)break;
		Totalcost+=dist[v];
		cnt++;
		dist[v]=0;//收录后dist的值要变为0，表明该结点v已被收录 
		for(int i=1; i<=N; i++){
			if(dist[i]!=0&&C[v][i]<dist[i]){
				dist[i]=C[v][i];
				parent[i]=v;
			}
		}
	}
	if(cnt==N)printf("%d", Totalcost);//如果所有结点都收录完毕，则输出总费用 
	else printf("-1");//否则，则说明有些该图里面有回路 ，无法生成树 
	
}
int main(){
	scanf("%d%d", &N, &M);
	//初始化各边 
	for(int i=1; i<=N; i++){
		for(int j=1; j<=N; j++){
			 C[i][j]=INFINITY;
		}
	}
	int a, b, c;
	for(int i=1; i<=M; i++){
		scanf("%d%d%d", &a, &b, &c);
		C[a][b]=C[b][a]=c;
	}
	Prim(1);
	return 0;
}