二分图判定

二分图判定是指给定一个具有 n 个顶点的图，要给图上每个顶点染色，并且要使相邻的顶点颜色不同。问是否能用最多 2 种颜色进行染色？保证图中没有重边和自环。

 把相邻顶点染成不同颜色的问题叫做图的着色问题。对图进行染色所需要的最小颜色数称为最小着色数。最小着色数是 2 的图称作二分图。

例如：

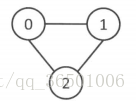
上图显然不是一个二分图，因为三个顶点两两相连，至少需要三种不同颜色；

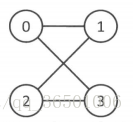
而这个图显然是一个二分图，只需要满足0、2是一种颜色，1、3是另一种颜色即可。

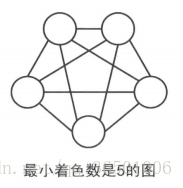
显然完全图  的最小着色数必为 n（当然只能为 n ）。当地 i 个点为第 i 种颜色后，第 i + 1 个点必然不能为前 i 种颜色，因为这 n 个点两两相连，因此共需要 n 种颜色。

如果只用 2 种颜色，那么确定一个顶点的颜色之后，和它相邻的顶点的颜色也就随之确定了。因此，选择从任意一个顶点出发，依次确定相邻顶点的颜色，就可以判断是否可以被 2 种颜色染色了。

这个问题用深度优先搜索容易实现。

#include <iostream>
#include <algorithm>
#include <vector>
#define MAXN 10//定义最大节点数
using namespace std;
vector <int> G[MAXN];//用邻接表作为图的存储结构
int color[MAXN];//保存每个节点的颜色
int V,E;
void read(){
	for(int i = 0;i < E;i ++){
		int s,t;
		cin >> s >> t;
		G[s].push_back(t);
		G[t].push_back(s);
	}
}
bool dfs(int v,int c){
	color[v] = c;//给节点 v 染色为 c
	//依次对 v 相邻的点进行处理
	for(int i = 0;i < G[v].size();i ++){
		//如果相邻的点和自己颜色相同则则无法达成目标
		if(color[G[v][i]] == c) return false;
		//如果相邻的点没有染色，且对这个点染不同的颜色后，对之相邻顶点的搜索出现矛盾则无法达成目标
		if(color[G[v][i]] == 0 && !dfs(G[v][i],-c)) return false;
	}
	return true;//如果对所有相邻的点都染色成功则返回 true
}
void solve(){//对邻接表中的顶点依次进行搜索染色
	for(int i = 0;i < V;i ++){
		if(color[i] == 0){
			if(!dfs(i,1)){
				cout << "NO" << endl;
				return ;
			}
		}
	}
	cout << "YES" << endl;
}
int main(void)
{
	cin >> V >> E;
	read();
	solve();
	return 0;
}

对于连通图来说，只需要进行 1 次 dfs 即可，而对于非连通图，则需要进行多次 dfs ，这时 solve 函数中的 for 循环便起了作用。事实上，也可以通过这种方法来判断一个图是否为森林。