Morris遍历

Morris遍历

在学习树结构的过程中，不论是递归或者非递归方式实现的遍历，都需要用到很多额外的空间结构。递归遍历使用系统栈完成遍历，非递归使用自己构建的栈或队列来完成，今天学习的Morris遍历只需要很少的额外空间，它的空间复杂读为O(1)，时间复杂度仍然是O(N)就可以完成遍历。

Morris遍历用到的结构在学术上称为线索二叉树，利用二叉树中原本的空指针来作为遍历时的标志，以此达到节省空间的目的。

Morris遍历细节

假设来到当前节点cur， 开始时cur来到头节点位置

 1. 如果cur没有左孩子， cur向右移动(cur = cur.right)

 2. 如果cur有左孩子， 找到左子树上最右的节点mostRight：

            a.如果mostRight的右指针指向空， 让其指向cur，

               然后cur向左移动(cur = cur.left)

            b.如果mostRight的右指针指向cur， 让其指向null，

                然后cur向右移动(cur = cur.right)

3.  cur为空时遍历停止

Morris遍历过程

现在有一颗树如下图，cur为指针依次指向要遍历的节点。

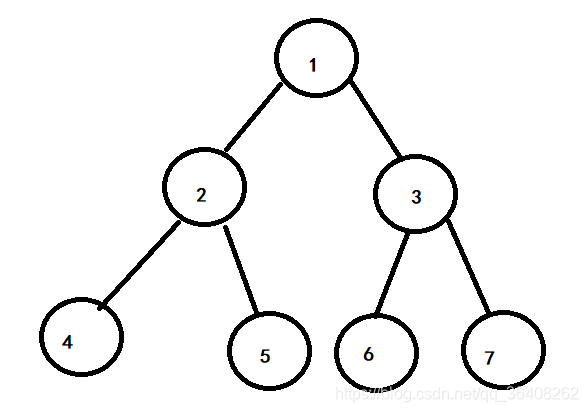
开始时cur指针指向1号节点，如下图

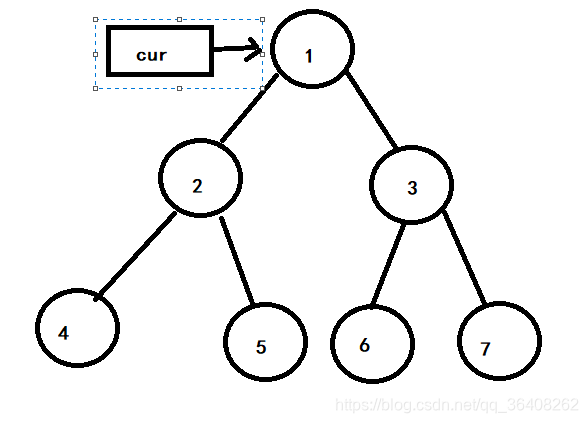
一号节点有左孩子，它的左子树的最右节点为5号节点，让5号节点指向cur指针指向的节点，即1号节点。cur指针向左移动，cur指针指向2号节点。如下图：

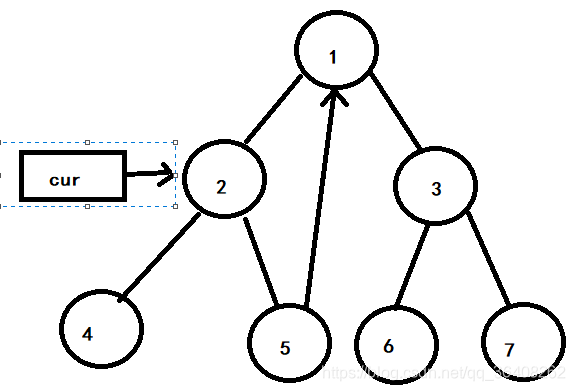
2号节点有左孩子，为4号节点。它的左子树的最右节点就是4号节点，所以让4号节点指向cur指向的节点，即2号节点，cur指针继续左移，现在cur指针指向4号节点。

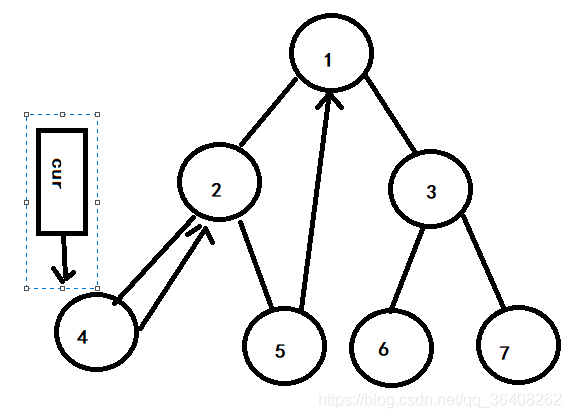
因为4号节点没有左孩子，所以cur向右移动，此时cur重新指向2号节点，如下图

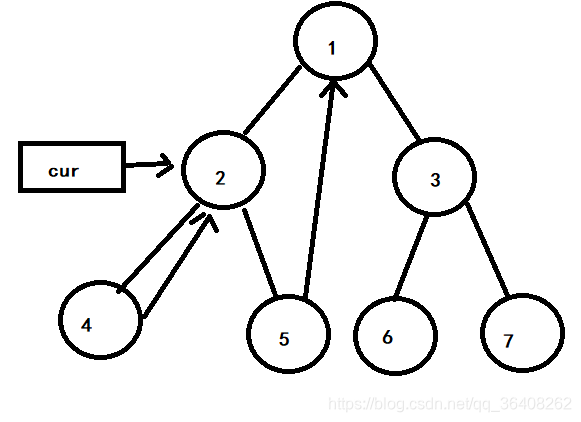
此时2号节点有左孩子（4号节点），且左子树的最右节点的右指针指向它自己，令左子树的有指针为NULL。cur继续向右移动，现在cur指向5号节点，如下图：

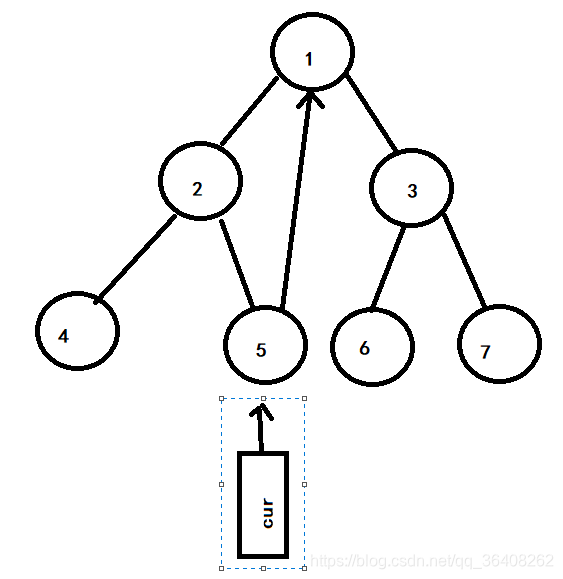
5号节点为叶子节点，没有左孩子，所以cur指针继续向右移动，cur指向1号节点。如下图

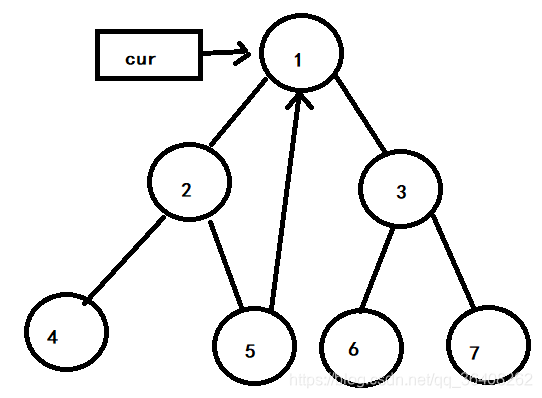
1号节点左子树的最右节点（5号节点）指向cur节点，所以令5号节点的右指针指向NULL，cur向右移动，现在cur指向3号节点。如下图

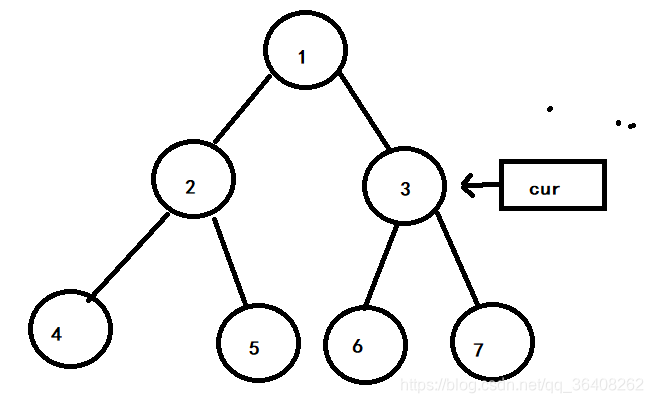
3号节点有左子树，左子树的最右节点为6号节点，所以令6号节点的右指针指向3号节点，cur指针向左移动。如下图：

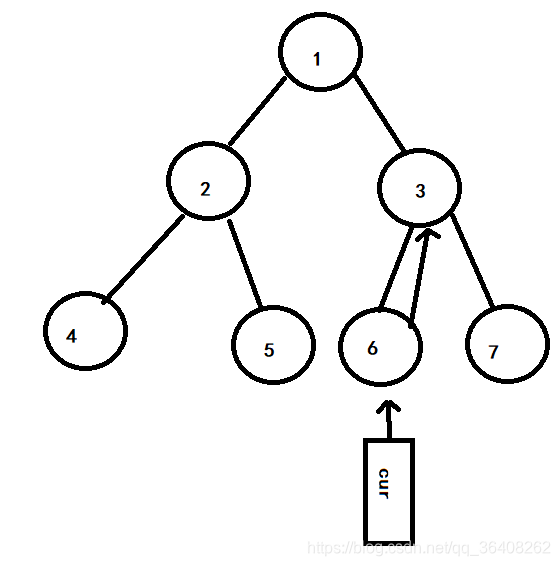
6号节点没有左孩子，所以cur指针继续向右移动，指向3号节点。如下图：

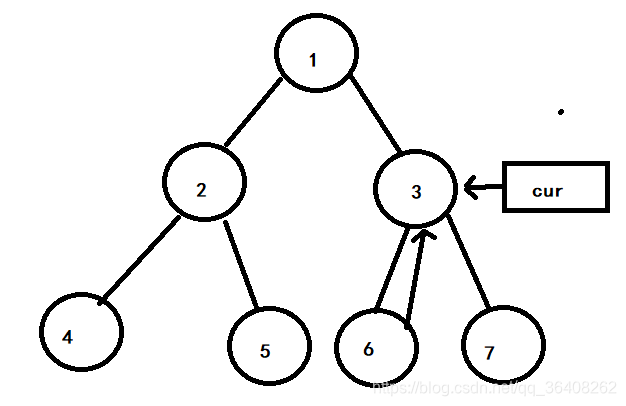
3号节点的左子树的最右节点为6号节点，它的有指针指向3号节点，所以令6号节点的右指针为空。cur向右移动，指向7号节点。如下图：

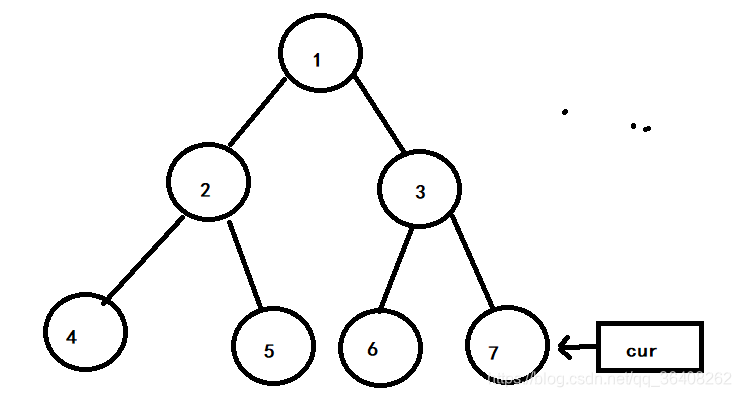
7号节点没有左孩子，cur指针继续向右移动，现在cur指针指向NULL，遍历结束。

对于上图中的树，morris遍历的过程为：1、2、4、2、5、1、3、6、3、7。

通过上述遍历，我们可以总结出以下规律：

1. 如果一个节点有左子树，那么它会在遍历过程中出现2次；
2. 如果一个节点没有左子树，那么它只会在遍历过程中出现1次；

同普通的遍历方式相比，节点出现的次数更少。对于普通的遍历，即使用系统栈或自己调用栈、队列的遍历过程，每一个节点都会出现3次。

代码实现

struct node{
    int data;
    node* left;
    node* right;
    node(int data){
        this->data = data;
        this->left = NULL;
        this->right = NULL;
    }
};

void morris(node* root){
    if(root == NULL){
        return;
    }
    node* cur = root;
    while(cur != NULL){
        cout << cur->data << endl;
        node* left = cur->left;
        if(left != NULL){
            while(left->right != NULL && left->right != cur){
                left = left->right;
            }
            if(left->right == NULL){
                left->right = cur;
                cur = cur->left;
                continue;
            }else{
                left->right = NULL;
            }
        }


        cur = cur->right;
    }
}

通过morris遍历可以改出前序、中序与后序遍历，且所需额外空间仍是常数级别的。

前面已经提到，morris遍历中有些节点会出现1次，有些节点会出现2次。所以只要将所有节点第一次出现时就输出节点，就是前序遍历。

代码实现：

//前序遍历
void  morrisPre(node* root){
    if(root == NULL){
        return;
    }
    node* cur = root;

    while(cur != NULL){
       // cout << cur->data << ":  "<< endl;
        node* left = cur->left;
        if(left != NULL){//morris遍历中会出现两次的节点
            while(left->right != NULL && left->right != cur){
                left = left->right;
            }
            if(left->right == NULL){//节点第一次出现
                cout << cur->data << endl;
                left->right = cur;
                cur = cur->left;
                continue;
            }
            left->right == NULL;
        }else{//morris中只会出现一次的节点
            cout << cur->data << endl;
        }
        cur = cur->right;
    }

}

对于中序遍历，只要将会出现两次的节点在其第二次出现时输出，其余节点同前序遍历即可。

//morris中序遍历
void morrisIn(node* root){
    if(root == NULL){
        return;
    }
    node* cur = root;
    while(cur != NULL){
        node* left = cur->left;
        if(left != NULL){
            while(left->right != NULL && left->right != cur){
            left = left->right;
            }
            if(left->right == NULL){
                left->right = cur;
                cur = cur->left;
                continue;
            }else{
                cout << cur->data << endl;
                left->right = NULL;
                cur = cur->right;
            }
        }else{
            cout << cur->data << endl;
            cur = cur->right;
        }

    }
}

对于后续遍历，因为二叉树中没有左子树的节点只会出现一次，所以不能直接输出这些节点。需要将在morris遍历中会出现2次的节点找出，在这些节点第二次出现时，逆序打印该节点左子树的有边界。当这些节点遍历完后，逆序打印整颗树的有边界。

对于如下图的一棵树

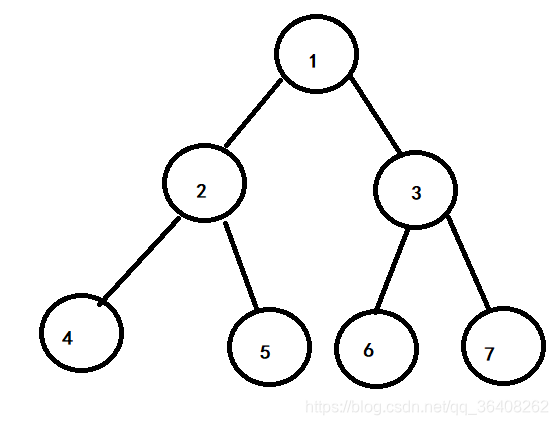
它的morris遍历过程为：1、2、4、2、5、1、3、6、3、7.

其中出现两次的节点的第二次出现的顺序为2、1、3。

逆序打印对应节点的左子树的有边界：

1. 4
2. 2、5
3. 6
4. 1、3、7

最后需要解决的问题是，怎样逆序打印右边界呢？之前做过反转链表的题目，现在可以套用到这里，只需要将以每个节点右孩子形成的边界反转两次即可。

//后序遍历
node* reverseList(node* head){
    node* next = NULL;
    node*pre = NULL;
    while(head != NULL){
        next = head->right;
        head->right = pre;
        pre = head;
        head = next;
    }
    return pre;
}

void printList(node* head){
    for( ; head != NULL; head = head->right){
        cout << head->data << endl;

    }
}

void MorrisPos(node* root){
     if(root == NULL){
        return;
    }
    node* cur = root;
    while(cur != NULL){
        node* left = cur->left;
        if(left != NULL){
            while(left->right != NULL && left->right != cur){
            left = left->right;
            }
            if(left->right == NULL){
                left->right = cur;
                cur = cur->left;
                continue;
            }else{
                left->right = NULL;
                node* temp = reverseList(cur->left);
                printList(temp);
                cur = cur->right;
                reverseList(temp);
            }
        }else{
            cur = cur->right;
        }

    }
    node* temp = reverseList(root);
    printList(temp);
    reverseList(temp);
}

morris的遍历有很多应用，但因为morris对一个节点最多只会经过2次，所以如果我们需要在第三次经过时进行业务处理的话，就不能使用morris了。