KMP和Manacher

KMP

KMP算法用来确定一个字符串是不是另一个字符串的子串，如果是返回子串所在开始位置的下标，否则返回-1。

如果使用暴力方法，我们确定目标字符串是不是原字符串的子串的方法为：从源字符串下标为0的位置与目标字符串的每个字符比对，当到达目标字符串结尾时，说明目标字符串是源字符串的子串，否则从源字符串下标为1的位置继续与目标字符串比对，当源字符串的剩余字符数比目标字符串的长度小时，则说明目标字符串不是源字符串的子串。如果源字符串的长度为n，目标字符串的长度为m，那么这个算法的时间复杂度为O(m*n)。

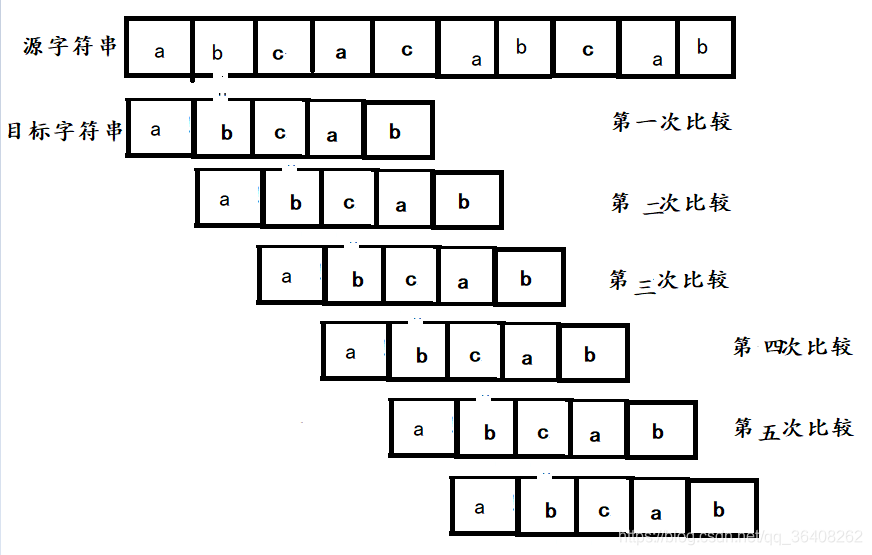
但从中可以发现这里有很多不必要的比较过程，在第一次比较的时候，0、1、2、3、位置上目标字符串和源字符串的字符都相等，而且目标字符串本身0和1上的字符是不相等的，所以第二次比较完全可以不进行，第三次比较同理，直接进行第四次比较。

KMP算法就是为了过略这些不必要的操作，它的时间复杂度为O（N）。而能够减少多少次操作，取决于目标字符串本身的性质。首先要介绍kmp算法中的一个概念，字符串中某个字符的前面的字符串中相等最长前缀和最长后缀的长度(前后缀长度相等)。我们分析字符串（”ababc“），首先选中字符c，那么它的前缀和后缀有（a,b）,(ab,ab),（aba,bab）三组，所以c在这个字符串中的相等的最长前后缀为ab，长度为2。对于一个字符串，除了第一个位置外，我们都可以求出后面每个位置的最长前后缀的长度，对于第一个字符，人们把他设置为-1。所以对于字符串“ababc”,可以得到一个关于该字符串上每个位置的最长前后缀的数组，next[],“ababc”的next数组为[-1,0,1,2,0]。

介绍过next数组后就可以来看KMP算法的比较过程，首先假设我们已经得到了目标字符串的正确的next数组。当源字符串和目标字符串分别在i和0位置开始比较，假设k位置出现不相等的字符，那么暴力求解需要源字符串退回到 i + 1位置，目标字符串回到0位置开始比较，而kmp算法则让源字符串的比较在k位置保持不动，目标字符串的比较指针回退到0 + next[k]位置，两者开始比较。

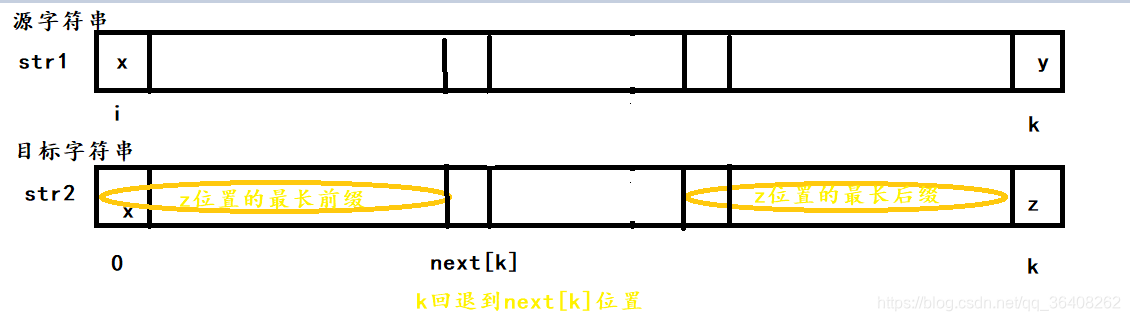
也就是说，源字符串再一次和目标字符串的比较如下：

从图中可以很明显的看出来，kmp算法如果确定源字符串中能够找到子串，也和暴力方法一样需要将目标字符串的全部字符与源字符串中从特定位置开始到目标串长度的字符比较一遍，上图kmp算法源字符串是从k-next[k]位置和目标字符串的0位置开始比较的，但因为上一次比较时已经证明了源字符串(k-next[k]) 到k - 1位置与目标字符串的0-next[k]位置是相等的，所以源字符串的比较指针不需要移动，目标字符串的比较指针也不需要回退到开始位置。

我们已经说明了目标字符串从next[k]位置、源字符串从k位置开始比较可以确定字串，那从源字符串的i + 1位置到k - next[k]位置开始就不能确定字串吗？这里可以先假设从a位置开始可以确定目标字符串是源字符串的子串。

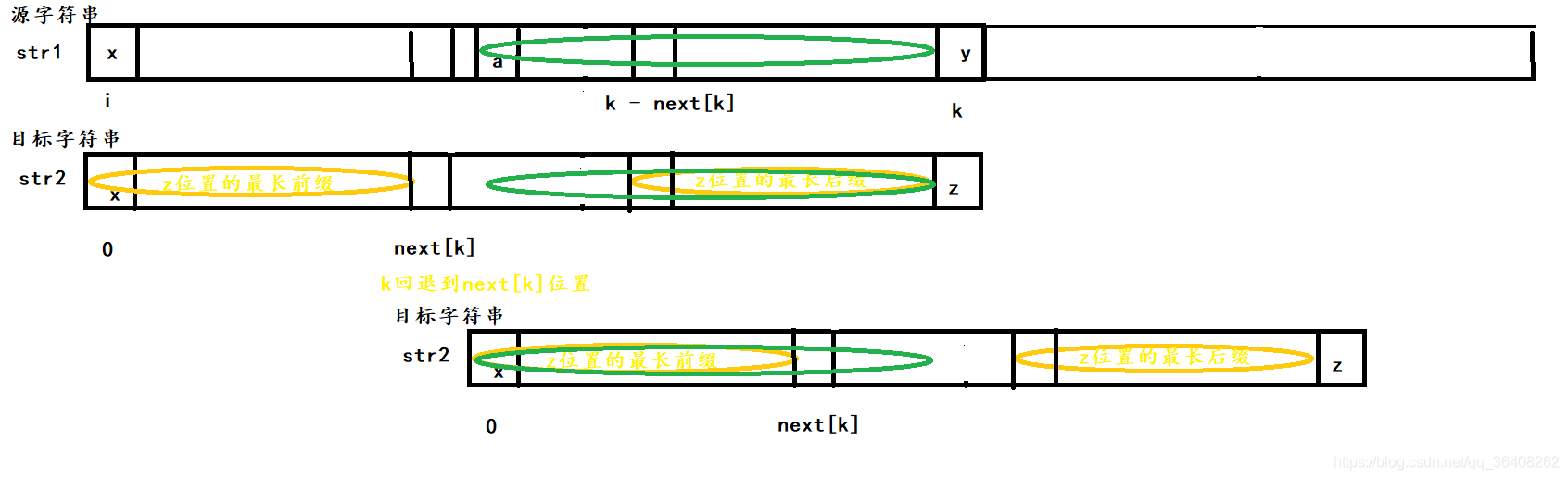
因为源字符串和目标字符串之前经过一次比较，所以前两块绿色部分一定相等，又因为我们假设a可以确定子串，所以第一块和第三块的绿色部分也相等。也就是说，目标子串在k位置的最长前缀和最长后缀不是我们之前求的next[k]，而存在一个比next[k]还要长的前缀和后缀，next[k]数组求错了。由此反推出a位置不可能求出子串，k-next[k]位置前的任何位置都不可能求出子串。

next数组的求法

当目标字符串的长度大于1的情况下，next[0] = -1, next[1] = 0,这两个可以直接设置。其中0位置是人为规定，1位置因为前面只有一个字符，而最长前后缀的长度不能等于它本身，所以next[1]只能等于0。对于next[2]的判断，则要看0位置和1位置上的字符是否相等，相等为1，否则为0。

对于next[i]，需要比较目标字符串next[i - 1] 位置是否与源字符串的i - 1位置相等，相等则next[i] = next[i - 1] + 1，否则需要从next[i - 1]位置向0位置方向移动，接下来移动到 next[next[i - 1]]  (下图的t位置)位置与i位置的字符比较，相等则next[i] = next[i - 1]+1;如果还不相等，则移动到next[next[t]] 位置,此时该值为0，next[i]的值为0。

代码实现

#include <iostream>
#include <string>
using namespace std;

//得到目标字符串的nexts数组
//数组中存储str每个位置相等的最长前缀和后缀的长度
int* getNexts(string str){
    if(str.size() == 1){
        int* arr = new int(-1);
        return arr ;
    }
    if(str.size() <= 0){
        return NULL;
    }
    int* nexts = new int[str.size()];
    nexts[0] = -1;
    nexts[1] = 0;
    int i = 2;//当前要求最长前后缀的位置
    //cur代表要和i - 1位置比对的字符的下标（i - 1位置前缀的下一个）
    //也代表i - 1位置前缀的长度
    int cur = 0;
    while(i < str.size()){
        if( str[cur] == str[i - 1]){
            nexts[i++] = ++cur;
        }else if(cur == 0){
            nexts[i++] = 0;
        }else{
            cur = nexts[cur];
        }
    }
    return nexts;
}
//KMP算法的实现
//str1 源字符串
//str2 目标字符串
//返回值:  目标字符串在源字符串中起始位置的下标,没有返回-1
int isIndexOf(string str1,string str2){
    if(str1.size() < str2.size()){
        return -1;
    }
    int* nexts = getNexts(str2);
    unsigned int i = 0,j = 0;
    for(; i < str1.size() && j < str2.size();){
        //cout << i << " " << j << endl;
        if(str1[i] == str2[j]){
            i++;
            j++;
        }else if(nexts[j] == -1){
            i++;
        }
        else{
            j = nexts[j];
        }
    }
    delete nexts;
    return j == str2.size() ? i - j : -1;
}






int main()
{
    string str1 = "fsadjkljfdskajfhjaabkkkaabtaabkkkaabpqmADSDasffDsf";
    string str2 = "aabkkkaabtaabkkkaab";
    int res = isIndexOf(str1,str2);
    cout << res <<endl;

    return 0;
}

 

那么kmp算法是怎样做到时间复杂度为O(N)？

在忽略next数组的情况下，由上面的分析可知，在两个字符串的比对过程中，源字符串的比较指针是不会回退的，设为x，而目标字符串的比较指针（设为y）会有回退的情况，所以需要构造一个一直增加的变量，这里取x - y。x的最大值为N，x - y的最大值也是N，所以操作量为2N，时间复杂度为O(N)。

Manacher

manacher算法用来求一个字符串的最长回文子串的长度。

暴力方法求解最长回文子串：遍历字符串，依次以每个字符为中心，比较它两边的字符是否相等，相等则继续比较左右两边的字符，否则继续遍历。将求得的结果中最大的值返回。但该方法只能求出回文为奇数的字符串，如”1221“不能求出。对于这个问题，可以依次在字符串中添加字符，如“#1#2#2#1#”，使用上述方法求解。暴力方法的时间复杂度为O(N^2)。

manacher方法可以将时间复杂度压缩到O(N)。对于回文子串的判定过程与暴力方法相同，但在获取字符的回文半径时有加速。

在使用manacher算法时很多卫视不需要挨个比较中心点的两边的字符。假设要求上图i位置的最长回文子串的长度，且i以前所有位置的最长回文子串都已经求的，其中黄色部分代表a位置的最长回文子串，绿色部分代表b位置的最长回文子串，则i位置的最长回文子串可以直接确定（下图蓝色部分）。因为i和a关于b中心对称，所以以i为中心的字符串等于以a为中心的字符串的倒叙，又因为以a为中心的字符串是回文，所以以i为中心的字符串也是回文。既然a的最长回文子串为黄色部分，则黄色边界左右两边的首字符不相等，关于b中心对称后，蓝色边界两边的首字符也不相等，以i为中心的最长回文子串可以直接确定。

首先需要了解回文半径和回文直径，如果由一个回文字符串如“121”，它的回文半径为2、回文直径为3；字符串“1221”分别为2、4；还需要了解比对的最右回文右半径（R），如字符串“#1#2#2#1#”，在寻找它的最长回文子串时，设R的初始值为-1，c为更改R时的回文中心点，设i字符串的数组下标依次遍历，则当i = 0时，c = 0，R = 1（以0位置为中心回文子串就是它本身 ）；当i = 1时，c = 1,R = 2（1位置的回文在2处结束）；当i = 2时，R = 2（以位置2为中心没有没有回文，所以取1的回文右边界）,c = 1......

manacher在获取某个位置（i）到最长回文子串时主要使用到最右比对的回文有半径（R）、确定R的中心点C、与i关于C中心对称的点j。所以根据i与R的相对位置，可以分为i在R内（可以与R重合）与i在R外两类。当i在R内时，根据j的位置，又可以分为三类，分别是j确定的最长回文子串的左边界在R的左边界的里面、外面与二者重合。下图为i在R内的三种情况。

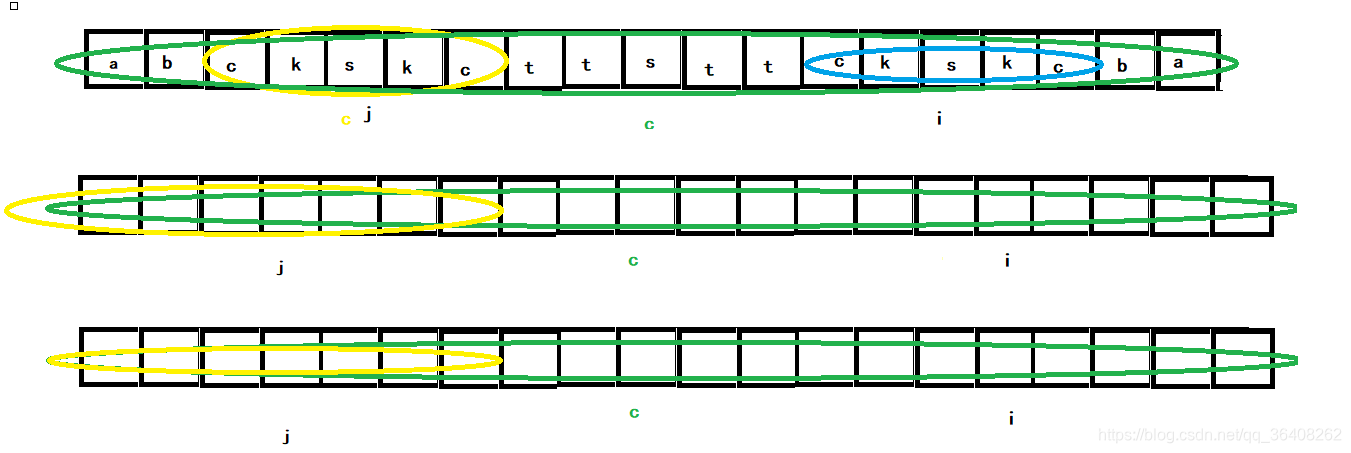
当i在R外时，只能暴力比较；当i在R内时，情况有如上三种：第一种如上所说可以直接确定i的最长回文半径，与j的长度相等；第二种同样可以直接确定，首先蓝色方框中的字符一定是以i为中心的回文，又因为a = b,b = c,a != d,所以c!= d。也就是说i的最长回文区域就是蓝色方框，最长回文半径的值为R - i；

 

第三种情况如下图，蓝色方框可以确定为i的回文，但a和b以及后面的字符是否相等需要比较，多以这种情况下i的最长回文子串的半径最少为j的最长回文子串的半径。

代码实现

#include <iostream>
#include <string>

using namespace std;

//依次在字符串str的每个字符前后添加“#”
string manacherString(string str){
    string s;
    for(unsigned int i = 0; i < str.size(); i++){
       s.append("#");
       s.append(1,str[i]);
    }
    s.append("#");
    return s;
}

int manacher(string str){
    if(str.size() == 0)
        return 0;
    //回文半径右边界的下一个位置
    int R = -1;
    //R的中心点
    int c = -1;
    string s = manacherString(str);
    int res = INT_MIN;
    int length[s.size()];
//按四类情况进行统计
//    for(int i = 0; i < s.size(); i++){
//        if(i >= R){
//
//            int rIndex = i + 1;
//            int lIndex = i - 1;
//            length[i] = 1;
//            for( ; rIndex < s.size() && lIndex >= 0 && s[rIndex] == s[lIndex]; rIndex++,lIndex--){
//                length[i]++;
//            }
//            R = rIndex;
//            c = i;
//        }else if(length[2 * c - i] < (R - i)){
//            length[i] = length[2*c - i];
//
//        }else if(length[2 * c - i] > (R - i)){
//            length[i] = R - i;
//        }else{
//            length[i] = length[2 * c - i];
//            int rIndex = R;
//            int lIndex = 2*i - R;
//            for( ; rIndex < s.size() && lIndex >= 0 && s[rIndex] == s[lIndex]; rIndex++,lIndex--)
//                length[i]++;
//            if(rIndex > R){
//                R = rIndex;
//                c = i;
//            }
//        }
//        res = length[i] > res ? length[i] : res;
//    }

    for(int i = 0; i < s.size(); i++){
        length[i] = i < R ? min(length[2 * c - i],R - i) : 1;
        while(i + length[i] < s.size() && i - length[i] > -1){
            if(s[i + length[i]] == s[i - length[i]])
                length[i]++;
            else{
                break;
            }
        }
        if(i + length[i] > R){
            R = i + length[i];
            c = i;
        }
        res = max(res,length[i]);
    }
    return res;
}

int main()
{
    string str = "abcba";
    cout << manacher(str);
    return 0;
}