上一篇对二叉树的建立和递归遍历都已经基本掌握了,为了提高效率要掌握非递归遍历。遍历的方法有很多,书中的代码段也不大相同,我自己总结并用代码实现了自己看着比较简单清晰的,这样以后用起来就很方便了。其实有有些代码看着比较晦涩难懂,解决的最简单的方法就是用例子,按着代码一步一步走,走通了基本也就理解了,然后在归纳思路。由特殊到一般。
二叉树先序的非递归算法:
void preorder1(BTNode *p)
{
int top=-1;
int maxsize=10;
BTNode *Stack[maxsize];
BTNode *q;
Stack[++top]=p;//根节点入栈
while(top!=-1)
{
q=Stack[top--];
cout<<q->data<<" ";
if(q->rchild!=NULL)//如果右孩子不为空
{
Stack[++top]=q->rchild;//右孩子进栈
}
if(q->lchild!=NULL)
{
Stack[++top]=q->lchild;
}
}
}
这面需要注意的就是,右孩子先进栈,左孩子后进栈,所有出栈的顺序相反正好是我们需要的顺序。
二叉树中序非递归遍历
void inorder1(BTNode *p)
{
if(p!=NULL)
{
int top=-1;
int maxsize=10;
BTNode *Stack[maxsize];
BTNode *q;
q=p;
while(top!=-1||q!=NULL)
{
while(q!=NULL)//左孩子存在,左孩子如栈
{
Stack[++top]=q;
q=q->lchild;
}
if(top!=-1)//栈不空
{
q=Stack[top--];
cout<<q->data<<" ";//输出节点
q=q->rchild;//指向右孩子
}
}
}
}
程序步骤:
1.开始根节点如栈
2.循环执行如下操作:如果栈顶节点左孩子存在,则左孩子如栈;如果左孩子不存在则出栈并输出栈顶结点,然后检查其右孩子书否存在,如果存在,则右孩子进栈。
二叉树后续非递归遍历
后续非递归遍历应该是属于这三种里面最难的了,前面两种很直观的就看懂了,后续遍历,书上有两种方法,就是定义一个栈和两个栈的区别,其实还挺有意思的。
先说一说两个栈的

先序遍历:1 2 4 5 3 6
后续遍历:4 5 2 6 3 1
逆后续:1 3 6 2 5 4
开始找规律,逆后续 ,1节点下面左子树245与右子树36交换然后2节点的4和5交换,这样就和前序一样了。佩服能找到这个规律的大佬,有趣是有趣,不过的确很难想到。所有需要两个栈,stack1用来辅助做逆后续遍历,将结果压入另一个栈stack2,将stack2的元素输出。
void postorder1(BTNode *p)//用两个栈的非递归
{
if(p!=NULL)
{
int maxsize=10;
BTNode *Stack1[maxsize];
BTNode *Stack2[maxsize];
int top1=-1,top2=-1;
BTNode *q=NULL;
Stack1[++top1]=p;
while(top1!=-1)
{
q=Stack1[top1--];
Stack2[++top2]=q;
if(q->lchild!=NULL)
{
Stack1[++top1]=q->lchild;
}
if(q->rchild!=NULL)
{
Stack1[++top1]=q->rchild;
}
}
while(top2!=-1)
{
q=Stack2[top2--];
cout<<q->data<<" ";
}
}
}
再说一个栈的,后续遍历访问的顺序,先访问左子树在访问右子树最后访问根节点。用栈存储节点时,要分清返回根节点的是从左子树返回的还是从右子树返回的,要用一个辅助指针标记一下。
void postorder2(BTNode *p)
{
int maxsize=10;
int top=-1;
BTNode *Stack[maxsize];
BTNode *q=NULL;
while(p!=NULL||top!=-1)
{
if(p!=NULL)
{
Stack[++top]=p;
p=p->lchild;
}
else
{
p=Stack[top];
if(p->rchild!=NULL&&p->rchild!=q)//如果右子树存在且没有被访问
{
p=p->rchild;
Stack[++top]=p;
p=p->lchild;
}
else
{
p=Stack[top--];
cout<<p->data<<" ";
q=p;//标记访问过的节点
p=NULL;
}
}
}
}
上面就解决了非递归的算法。
还有一种层次遍历,这种遍历最直观,一层一层的拨开它的心。从上到下,从左往右。就不多说了。
void level(BTNode *p)
{
int Front=0,Rear=0;
int maxsize=10;
BTNode *que[maxsize];//存放的是结点的指针
BTNode *q=NULL;
if(p!=NULL)
{
Rear=(Rear+1)%maxsize;
que[Rear]=p;//根节点入队
while(Front!=Rear)
{
Front=(Front+1)%maxsize;
q=que[Front];
cout<<q->data<<" ";
if(q->lchild!=NULL)
{
Rear=(Rear+1)%maxsize;
que[Rear]=q->lchild;
}
if(q->rchild!=NULL)
{
Rear=(Rear+1)%maxsize;
que[Rear]=q->rchild;
}
}
}
}
按照以往的风格,还是要有一份完整的代码这样更加直观
#include <iostream>
#include <stdlib.h>
using namespace std;
typedef struct BTNode
{
char data;//数据域,这里的节点类型为char,可以修改成其他类型
struct BTNode *lchild;//左指针域
struct BTNode *rchild;// 右指针域
}BTNode;
BTNode* createBitree()//前序顺序建立二叉树
{
BTNode*p;
char c;
cin>>c;
if(c=='0')
{
p=NULL;
}
else
{
p=new BTNode;//C++中开辟新的结构体空间
//p =(BTNode*)malloc(sizeof(BTNode));//C语言中的用法,要包含stdlib.h这个头文件
p->data=c;
p->lchild=createBitree();
p->rchild=createBitree();
}
return p;
}
void preorder(BTNode *p)
{
if(p!=NULL)
{
cout<<p->data<<" ";
preorder(p->lchild);
preorder(p->rchild);
}
}
void preorder1(BTNode *p)
{
int top=-1;
int maxsize=10;
BTNode *Stack[maxsize];
BTNode *q;
Stack[++top]=p;//根节点入栈
while(top!=-1)
{
q=Stack[top--];
cout<<q->data<<" ";
if(q->rchild!=NULL)
{
Stack[++top]=q->rchild;
}
if(q->lchild!=NULL)
{
Stack[++top]=q->lchild;
}
}
}
void inorder(BTNode *p)
{
if(p!=NULL)
{
inorder(p->lchild);
cout<<p->data<<" ";
inorder(p->rchild);
}
}
void inorder1(BTNode *p)
{
if(p!=NULL)
{
int top=-1;
int maxsize=10;
BTNode *Stack[maxsize];
BTNode *q;
q=p;
while(top!=-1||q!=NULL)
{
while(q!=NULL)
{
Stack[++top]=q;
q=q->lchild;
}
if(top!=-1)
{
q=Stack[top--];
cout<<q->data<<" ";
q=q->rchild;
}
}
}
}
void postorder(BTNode *p)
{
if(p!=NULL)
{
postorder(p->lchild);
postorder(p->rchild);
cout<<p->data<<" ";
}
}
void postorder1(BTNode *p)//用两个栈的非递归
{
if(p!=NULL)
{
int maxsize=10;
BTNode *Stack1[maxsize];
BTNode *Stack2[maxsize];
int top1=-1,top2=-1;
BTNode *q=NULL;
Stack1[++top1]=p;
while(top1!=-1)
{
q=Stack1[top1--];
Stack2[++top2]=q;
if(q->lchild!=NULL)
{
Stack1[++top1]=q->lchild;
}
if(q->rchild!=NULL)
{
Stack1[++top1]=q->rchild;
}
}
while(top2!=-1)
{
q=Stack2[top2--];
cout<<q->data<<" ";
}
}
}
void postorder2(BTNode *p)
{
int maxsize=10;
int top=-1;
BTNode *Stack[maxsize];
BTNode *q=NULL;
while(p!=NULL||top!=-1)
{
if(p!=NULL)
{
Stack[++top]=p;
p=p->lchild;
}
else
{
p=Stack[top];
if(p->rchild!=NULL&&p->rchild!=q)
{
p=p->rchild;
Stack[++top]=p;
p=p->lchild;
}
else
{
p=Stack[top--];
cout<<p->data<<" ";
q=p;
p=NULL;
}
}
}
}
void level(BTNode *p)
{
int Front=0,Rear=0;
int maxsize=10;
BTNode *que[maxsize];//存放的是结点的指针
BTNode *q=NULL;
if(p!=NULL)
{
Rear=(Rear+1)%maxsize;
que[Rear]=p;//根节点入队
while(Front!=Rear)
{
Front=(Front+1)%maxsize;
q=que[Front];
cout<<q->data<<" ";
if(q->lchild!=NULL)
{
Rear=(Rear+1)%maxsize;
que[Rear]=q->lchild;
}
if(q->rchild!=NULL)
{
Rear=(Rear+1)%maxsize;
que[Rear]=q->rchild;
}
}
}
}
int main()
{
BTNode *T=NULL;
cout<<"请创建一个二叉树"<<endl;//例如:124000300
T=createBitree();
cout<<"二叉树创建完成!"<<endl;
cout<<"前序递归遍历二叉树"<<endl;
preorder(T);
cout<<endl;
cout<<"前序非递归遍历二叉树"<<endl;
preorder1(T);
cout<<endl;
cout<<"中序递归遍历二叉树"<<endl;
inorder(T);
cout<<endl;
cout<<"中序非递归遍历二叉树"<<endl;
inorder1(T);
cout<<endl;
cout<<"后序递归遍历二叉树"<<endl;
postorder(T);
cout<<endl;
cout<<"后序非递归遍历二叉树(两个栈)"<<endl;
postorder1(T);
cout<<endl;
cout<<"后序非递归遍历二叉树(一个栈)"<<endl;
postorder2(T);
cout<<endl;
cout<<"层次遍历二叉树"<<endl;
level(T);
return 0;
}
输出结果:
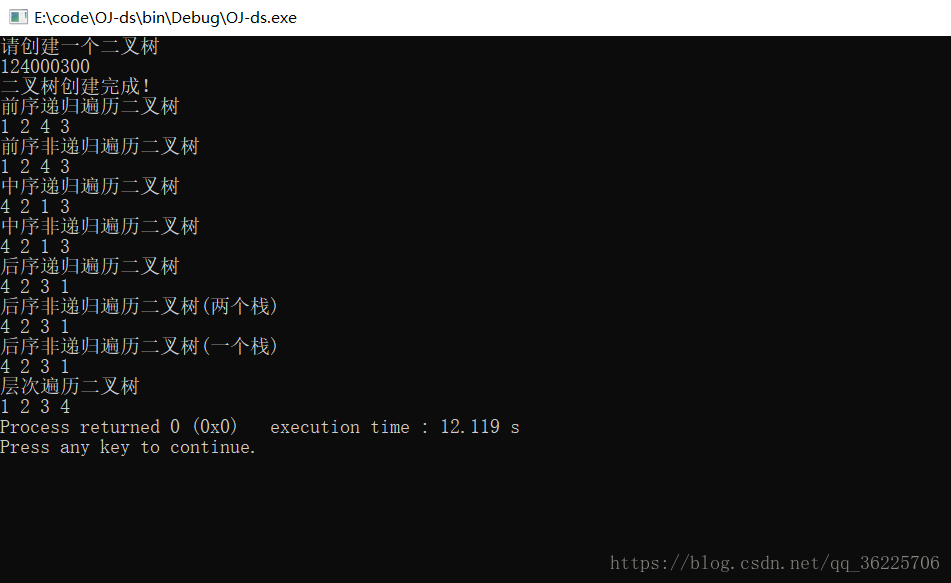
等我哪天做题坐累了,继续写,下篇见








 本文总结了二叉树的非递归遍历方法,包括先序、中序和后续遍历。通过具体的算法步骤和代码实现,帮助读者理解如何进行这些遍历。特别是后续遍历,通过两种不同栈的实现方式,揭示了其转换规律和难点。
本文总结了二叉树的非递归遍历方法,包括先序、中序和后续遍历。通过具体的算法步骤和代码实现,帮助读者理解如何进行这些遍历。特别是后续遍历,通过两种不同栈的实现方式,揭示了其转换规律和难点。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








