编译原理第二版习题3.9

Exercises for Section 3.9

3.9.1

Extend the table of Fig. 3.58 to include the operators

1. ？

Answer

node n	nullable(n)	firstpos(n)
n = c_1 ?	true	firstpos(c_1)
n = c_1 +	nullable(c_1)	firstpos(c_1)

3.9.2

Use Algorithm 3.36 to convert the regular expressions of
Ex­ercise 3.7.3 directly to deterministic finite automata.

Answer

1. (a|b)*

   • Syntax tree

     

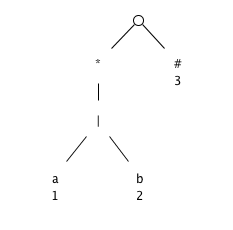
   • firstpos and lastpos for nodes in the syntax tree

     

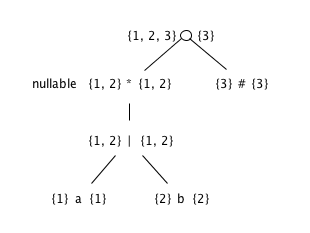
   • The function followpos

     node n	followpos(n)
     1	{1, 2, 3}
     2	{1, 2, 3}
     3	∅

   • Steps

     The value of firstpos for the root of the tree is {1, 2, 3}, so this set is the start state of D. Call this set of states A. We compute Dtran[A, a] and Dtran[A, b]. Among the positions of A, 1 correspond to a, while 2 correspond to b. Thus Dtran[A, a] = followpos(1) = {1, 2, 3}， Dtran[A, b] = followpos(2) = {1, 2, 3}. Both the results are set A, so dose not have new state, end the computation.

   • DFA

     

2. (a*|b*)*

3. ((ε|a)|b*)*

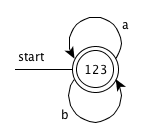
4. (a|b)*abb(a|b)*

3.9.3 !

We can prove that two regular expressions are equivalent by
showing that their minimum-state DFA’s are the same up to renaming of states.
Show in this way that the following regular expressions: (a|b)*, (a*|b*)*, and
((ε|a)b*)* are all equivalent. Note: You may have constructed the DFA’s for
these expressions in response to Exercise 3.7.3.

Answer

Refer to the answers of 3.7.3 and 3.9.2-1

3.9.4 !

Construct the minimum-state DFA’s for the following regular expressions:

1. (a|b)*a(a|b)
2. (a|b)*a(a|b)(a|b)
3. (a|b)*a(a|b)(a|b)(a|b)

Do you see a pattern?

3.9.5 !!

To make formal the informal claim of Example 3.25, show
that any deterministic finite automaton for the regular expression

(a|b)*a(a|b)…(a|b)

where (a|b) appears n - 1 times at the end, must have at least 2n states. Hint:
Observe the pattern in Exercise 3.9.4. What condition regarding the history of
inputs does each state represent?