中缀式、前缀式、后缀式相关

中缀式、后缀式、前缀式的定义

中缀式

是一个通用的算术或逻辑公式表示方法， 操作符是以中缀形式处于操作数的中间（例：3 + 4），中缀表达式是人们常用的算术表示方法。

后缀式

逆波兰式，这种表示方式把运算符写在运算对象的后面，例如，把a+b写成ab+，所以也称为后缀式。这种表示法的优点是根据运算对象和算符的出现次序进行计算，不需要使用括号，也便于用械实现求值。

前缀式

波兰式，前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，其将运算符写在前面，操作数写在后面。例如，- 1 + 2 3，它等价于1-(2+3)。

中缀式转化为后缀式、前缀式

中缀式转化为后缀式

方法一 :二叉树法

中缀式可以通过构造二叉树，并且后序遍历二叉树的方法求得后缀式，方法如下：

1. 找到中缀式中最后运算的运算符作为二叉树的根节点；
2. 将1中运算符左右两边的式子分别构造二叉树作为1中节点 的左右子树。如果式子中只剩下一个操作数，则将操作数作为叶子节点，如果式子中含有操作数和运算符，则利用1、2讲述的方法继续往下生成左右子树。直到所有叶节点均为操作数为止；
3. 将得到的二叉树进行后序遍历即可得到原中缀式的后缀式。

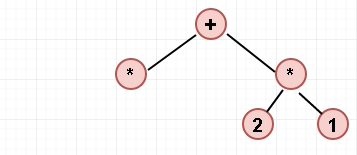
以中缀式 (1+2) * 3+2 * 1 为例示意图如下：