赛题题目:降低汽油精制过程中的辛烷值损失模型
小组成员:于泽华,路博文,康凯
本论文部分源码:GitHub - Zehua-Yu/2020Graduate-mathematical-modeling-B
本论文核心方法出自本人的文章:Z. Yu, X. Zheng, Z. Yang, B. Lu, X. Li and M. Fu, "Interaction-Temporal GCN: A Hybrid Deep Framework For Covid-19 Pandemic Analysis," in IEEE Open Journal of Engineering in Medicine and Biology, vol. 2, pp. 97-103, 2021, doi: 10.1109/OJEMB.2021.3063890.
PS:由于部分原因,并没有写出全部的论文内容及实验结果。
摘要
汽油是小型汽车的主要燃料,但其燃烧产生的尾气排放对大气环境有着重要的影响,将汽油清洁化已是迫在眉睫,但同时也要保证其辛烷值的含量。本文运用机器学习的方法针对处理辛烷值(RON)损失预测模型的问题展开研究。将工厂的原始样本数据进行预处理,分析在精制处理汽油的工程中辛烷值下降的原因,然后将全部的操作变量进行两种不同方法(随机森林和ARMA)的降维处理,对处理后留存下的主要变量进行建模,利用BP(Back Propagation)神经网络进行模型训练,经过验证和测试,利用随机森林和ARMA降维结果作为可变主要变量的产品RON预测准确率分别为:99.6%和99.2%。随即又针对模型输出对主要操作变量进行优化,并将输出结果进行可视化处理。最终,两个方法对应的最高优化RON损失降幅分别为63.21%和65.88%,均达到题目提出的超过30%的标准。
问题一:由于原始数据的采集过程中,可能有部分检测位点存在问题,部分检测时间点的数据出现异常,此外原始数据中还存在部分检测时间点数据精度不达标的情况,对于该部分也应予以剔除。本文依“样本确定方法”(附件二)对285号和313号数据样本进行预处理,在原始数据样本(附件三“285号和313号样本原始数据)的基础上进行数据筛选与处理。
问题二:工程技术应用中经常使用先对数据进行降维,然后建模的方法,这有利于忽略次要因素,发现并分析影响模型的主要变量与因素。本文同时为了降低后续数据处理过程中所消耗的计算资源,采用随机森林(RF)和自回归滑动平均模型(ARMA)两种方法,对354个操作变量进行筛选,使得筛选出的操作变量最具代表性,与目标对象的相关程度高。
问题三:针对本题目所给的场景与数据特点,本文基于BP神经网络结构针对辛烷值(RON)和硫含量双输出的预测模型进行设计。该神经网络具有良好的非线性映射和容错能力,十分契合数据集中的数据特点。此外,本文选择了相对合适的激活函数,以应对梯度消失和过拟合问题。
问题四:本文使用问题三中训练所得模型进行参数优化,优化目标是维持产品硫含量不大于5μg/g,并使产品RON的损失降幅超过30%。对于133号样本,我们使用步进参数优化方法,优化出使得RON损失降福最大约为65%的主要变量参数组合。
问题五:对133号样本优化过程与结果的可视化,并进行优化效果的具体分析,给出优化后产品RON的损失降幅,进而对模型性能进行评估。
关键词:特征降维;随机森林;自回归滑动平均模型;BP 神经网络
1.问题重述
1.1 问题背景
随着社会的发展,汽油燃料需求日益增加,燃烧其产生的尾气污染大气环境的问题也 日渐突显。辛烷值是反映汽油燃烧性能的重要指标,但由于现有脱硫技术的原因,在对汽 油进行处理时,都会降低其辛烷值,进而造成巨大的损失。为了汽油得到最优的利用,本 文在建模过程中研究如何满足操作变量的多样性、对原料分析的高要求及过程优化响应的 及时性。通过数据挖掘技术来建立汽油辛烷值(RON)损失的预测模型,按照每个样本约 束的优化操作的框架下,研究如何在满足汽油脱硫效果的同时(硫含量不大于 5μg/g), 实现降低汽油辛烷值损失在 30%以上。
1.2 需要解决的问题
在本文中,我们根据附件一的样本预处理结果数据、附件二的样本确定方法和附件三的两个原始数据样本进行建立辛烷值(RON)损失预测模型,并按要求完成如下问题:
(1) 参考附件一的工业数据的预处理结果,依照附件二中的样本确定方法对附件三中的原始样本数据进行预处理并将处理结果分别加入到附件一中的相应位置,供下述条件使用。
(2) 辛烷值的测量是测量时刻前两小时内操作变量的综合效果,所以要求预处理中取操作变量的平均值与辛烷值的测量值对应。
(3) 在建立降低辛烷值损失模型的过程中,要从367个操作变量中发现并分析影响模型的主要变量和因素,要求筛选出的建模主要变量为相对独立、对输出结果影响较大的操 作变量。按题目要求,从 354 个操作变量中选择出 27 个特征变量,加上原料的辛烷值 和硫含量共 29 个参数类别,作为该模型的主要操作变量和因素。
(4) 建立RON损失预测模型,采用附件中的样本和选择出的主要变量和因素,通过回归或 神经网络等技术,对问题所属的辛烷值损失预测模型进行建立,并用附件一数据对模 型进行验证。
(5) 要求在保证产品硫含量不大于5μg/g的前提下,利用上述模型以分析出的数据样本中, 获得 RON 损失降幅大于 30%的样本中对应的主要变量优化的操作条件。
(6) 要求对133号样本进行可视化展示,以图形展示其主要操作变量优化调整过程中对应的RON和硫含量的变化轨迹。
2. 模型假设
(1) 由附件一325个样本数据可见,各个样本的原料性质数据均有不同,故对不同样本进 行相同的相关操作变量数值调整时,产品中硫含量和辛烷值 RON 均不同。选定样本的 7 个原料性质数据作为输入,且在后续问题中同一个样本的原料性质均保持不变,即 7 个原料性质不可作为优化产品操作方案的因素和变量;
(2) 由于附件一中325个样本的操作变量数众多,其中包含一些与目标输出(产品硫含量 和产品辛烷值 RON)相关度较低的操作变量。为了降低模型计算量,提高效率,本文 拟对354个操作变量进行特征选择,从中筛选出与目标输出相关程度最大的10个操作 位作为整个预测模型的输入变量;
(3) 由上述1)和2)中进行的假设,本文中所设计的产品辛烷值预测模型的输入为样本的 7 个原料性质和 10 个操作为变量;
(4) 只考虑附件一中所给的样本数据;
(5) 在特征提取部分拟引入两类方法,在建模部分拟引入BP网络,在优化操作位部分拟使
用步进优化参数法。 根据以上假设,本题目的全部方法流程图如图2-1所示:
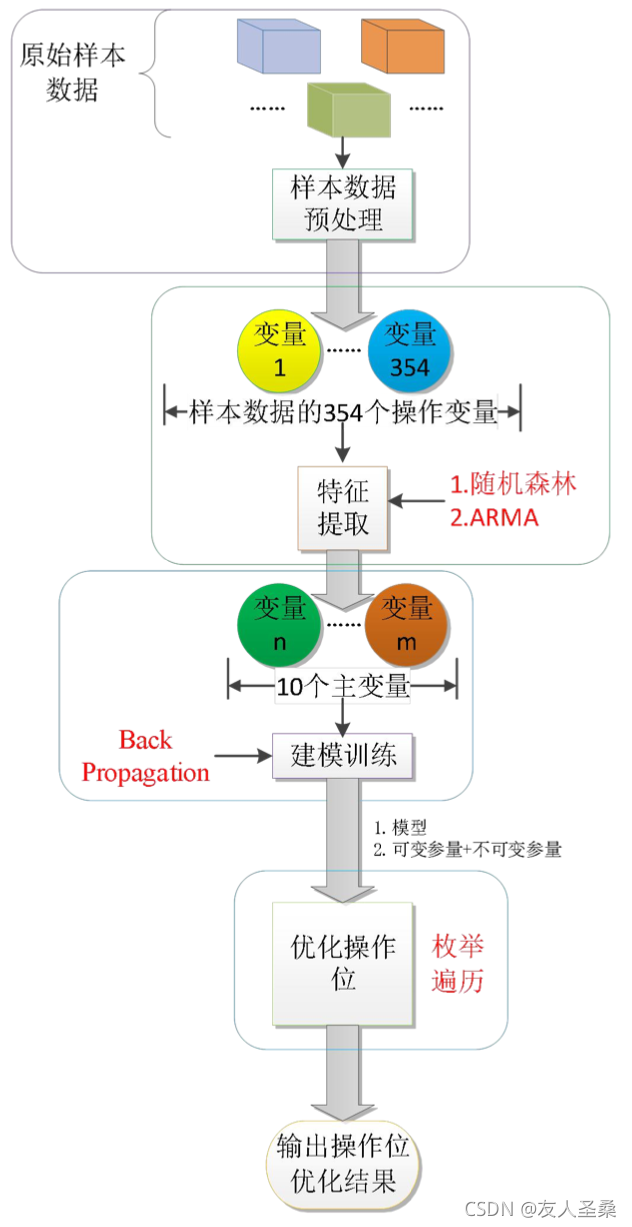
图2-1 整体框架流程图
3 问题一: 对 285 号和 313 号样本的原始数据进行处理
3.1 问题分析
由于原始数据的采集过程中,可能有部分检测位点存在问题,在部分检测时间点的数 据出现异常,此外原始数据中还存在部分检测时间点数据精度不达标的情况,对于该部分 也应予以剔除。附件一中的样本数据应该均符合相关要求,能够保证操作变量与产品输出 指标存在合理的相关性,从而使后续数据分析和相关建模工作更具有实际意义。
数据来源:原始数据采集来源于中石化高桥石化实时数据库(霍尼韦尔 PHD)及 LIMS 实验数据库。
问题要求:利用附件三所给的 285 号和 313 号样本的原始数据,依“样本确定方法” (附件二)对 285 号和 313 号数据样本进行预处理,并用处理后的数据对附件一对应样本 编号的数据进行更新。根据问题一要求对 285 号以及 313 号样本原始数据进行数据处理(原 始数据见附件三)。由附件二中关于数据整定的要求,对于 285 号和 313 号样本的原始数 据各个时间点的点位,若操作变量只含有部分时间点的位点,其残缺数据较多,无法补充, 则将此类位点删除;对于部分操作变量数据为空值的位点,空值处用其前后两个小时数据 的平均值代替;依据附件四中对各个原始数据的操作变量操作范围,采用最大最小的限幅 方法剔除一部分不在此范围的样本;根据拉依达准则(3σ准则)去除异常值。
目标:将附件三中 285 号和 313 号样本原始数据中不符合附件二中相关要求的参数进 行删除、代替或剔除异常值等操作,再对通过上述数据整定后的原始数据求其各个操作变 量的均值,并对附件一对应样本编号的数据进行更新。
数据预处理流程图如图3-1所示:
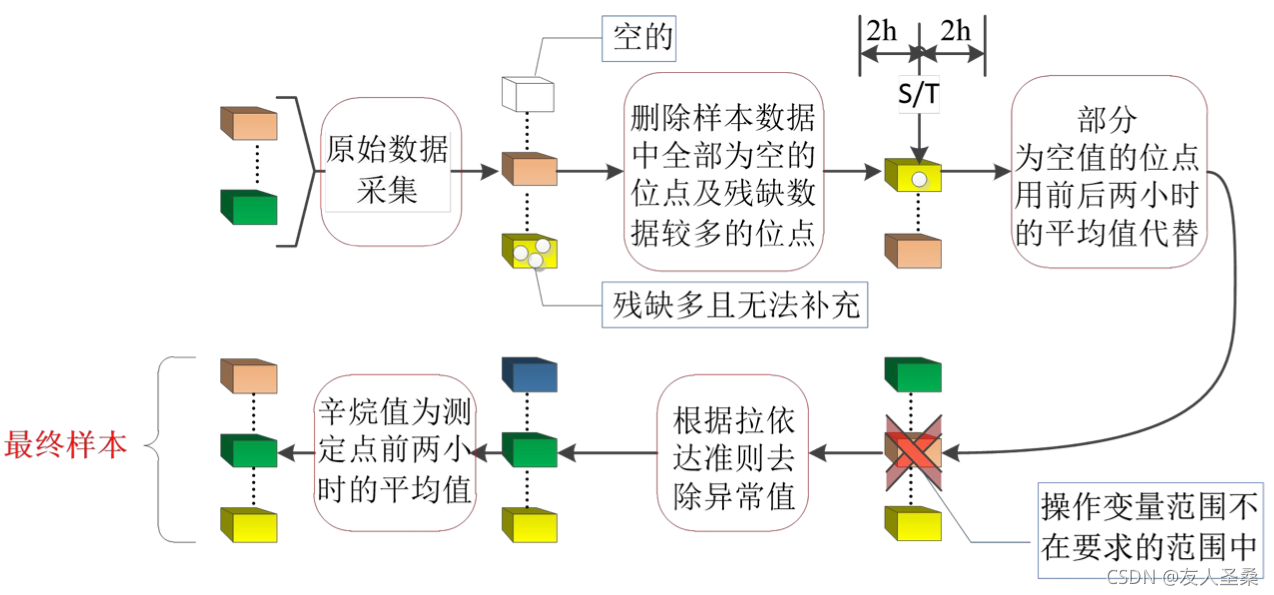
图3-1 数据预处理流程图
3.2 数据提取
导入附件三中 285 号和 313 号样本每个测试时间点各个操作变量的对应数值。原始数据中,大部分变量数据正常,但由附件二中可知,每套装置的数据均有部分位点存在问题, 需要对原始数据进行处理后才可以使用。
3.3 数据处理
(1) 删除285号和313号样本中残缺数据较多、无法进行补充的的操作变量(删除该位点)。 对 285 号和 313 号样本原始数据进行筛选,其中有若干操作变量在所有时间节点均无 数据,故将此类操作位点所有数值置零,从而表示删除该类操作位点。
(2) 对于部分操作变量数据为空值的位点,空值处用其前后两个小时数据的平均值代替。 对 285 号和 313 号样本原始数据进行筛选,均无满足该条件的数据,故不予处理。
(3) 依据附件四中对原始数据的操作变量操作范围,采用最大最小的限幅方法,从285号 和 313 号样本原始数据中剔除一部分不在此范围的样本。
(4) 根据拉依达准则(3σ准则)去除异常值。分别对285号和313号样本原始数据各个操 作变量进行等精度测量,对每个操作位点在 40 个时间节点得到 x1,x2,......,x40, 算出其算术平均值 x。其次根据对应操作变量的算数平均值,求出剩余误差 vi=xi-x (i=1,2,...,40)。再对每个操作变量按贝塞尔公式求出其对应的标准误差σ,贝塞尔公式如(1)所示:
若某个操作变量在b时间节点的测量值的剩余误差(1<=b<=n),满足
,则认为
是含有粗大误差值的坏值,285号样本和313号样本的原始数据中,各个操作变量均有部分时间节点的数据满足|vb|=|xb-x|>3σ,将该部分坏值剔除。
完成上述4步主要操作后,对285号和313号样本原始数据中各个操作变量求均值, 并将处理后的数据对附件一进行更新。
3.4 数据对比
由完成处理的数据,可以发现285号和313号样本数据与附件一中相同,说明附件一中所给的285号与313号样本操作变量数据均无坏值,符合工业生产中的观测要求。可以作为后续数据挖掘和分析工作的基础,能够作为参考样本反应操作变量和产品输出指标的关系。
4 问题二: 选取主要特征操作变量
4.1 问题分析
汽油的实际精制生产工序十分繁琐,可操作位点繁多,而不同操作位点之间可能存在着某些相关性质,例如装置内部温度的变化可能会导致装置内部压力的变化。同时也存在 一些与汽油成品质量相关性不大的常规操作变量。为了降低后续数据处理过程中所消耗的计算资源,需要对354个操作变量进行筛选,使得筛选出的操作变量最具代表性,与目标输出指标的相关程度高。
数据来源:原始数据采集来源于中石化高桥石化实时数据库(霍尼韦尔 PHD)及 LIMS 实验数据库。
问题要求:附件一中提供的 325 个样本数据中,包括 7 个原料性质、2 个待生吸附剂 性质、2 个再生吸附剂性质、2 个产品性质等变量以及另外 354 个操作变量(共计 367 个 变量)。对上述 367 个变量进行降维,选出不超过 30 个特征变量对模型进行建模。要求 选择具有代表性、独立性。
目标:由于附件一中的 325 个样本的原料性质均有差异,故本文将样本的 7 个原料性质作为模型输入的一部分,且对单个样本进行分析时原料性质不可进行操作更改。此外,本文将对 367 个操作变量进行特征选择,从中选择 10 个对模型输出影响较大的操作变量作为降维后的特征。综上所述,本文对上述 367 个变量(其中预先确定选择 7 个原料属性变量)选择合适的特征降维方法进行降维后,得到共 17 个特征。
4.2 特征降维简述
附件一中提供的325个样本数据中,包括7个原料性质、2个待生吸附剂性质、2个再生吸附剂性质、2个产品性质等变量以及另外354个操作变量(共计367个变量)。若将所有变量作为输入建立降低辛烷值损失模型,一方面会需要大量的计算资源,另一方面367个变量中存在一些与模型输出值相关性较低的变量,我们在建模前需要对这些变量进行筛选,发现并分析影响模型的主要变量与因素。使用降维后的操作变量,使得在工程应用上的相关操作更加方便。需要注意的是,上述的367个变量均对应独立的相关操作,题目要求改动和提取的也是原有操作位,故本文在进行特征降维时,不使用将原始特征映射到其他特征空间再进行主成分分析的方法,而是在上述367个变量中选择7个原料性质和10个可操作变量,作为影响模型最主要的可操作变量和单个样本因素。
常见特征降维方法与适用性分析:关于特征降维,目前有许多常见的方法PCA[[i]](Principal Component Analysis)、LDA[[ii]](Linear discriminant analysis) 、LLE[[iii]](Locally linear embedding)、ISOMAP[[iv]]、tSNE[[v]]、Perason相关系数[[vi]]和随机森林[[vii]]等等。
- PCA的基本思想就是寻找数据方差最大的方向作为主轴方向,由主轴构成一个新的坐标系,这里的维数可以比原维数低,然后数据由原坐标系向新坐标系投影,这个投影的过程就是降维的过程,作为一种线性降维的方法,并不适用于附件一中需要我们处理的大量非线性数据。
- LDA也是一种线性降维方法,其目的是最大化样本的类间距离和最小化样本的类内距离,其在分类和降维均有不错的效果,其被证明是非常有效的降维方法,其线性模型对于噪音的鲁棒性效果比较好,不容易过拟合。LLE是一种非线性降维算法,它能够使降维后的数据较好地保持原有流形结构,降维过程中不再关注样本方差,而是一种关注降维时保持样本局部的线性特征。
- ISOMAP与LLE类似,也是一种非线性降维算法,不同的是ISOMAP关注样本的全局结构信息。
- tSNE是由SNE衍生发展的一种降维算法,SNE将高维映射到低维的同时,尽量保证相互之间的分布概率不变,SNE将高维和低维中的样本分布都看作高斯分布,而TSNE将低维中的坐标当作T分布,这样的好处是为了让距离大的簇之间距离拉大,从而解决了拥挤问题。但是当输入样本较多时,会出现构建网络困难和梯度下降慢的问题。
Perason相关系数可作为衡量两个特征向量之间线性相关程度的系数。设X, Y为两个变量,为变量X和Y之间的perason相关系数,也就是两个变量的协方差与两个变量的标准差之积的比值,其范围区间为[-1, 1]。其绝对值越大则两变量之间的线性相关程度越强,
则两变量之间无线性相关性。使用perason相关系数可以很好的对与目标变量Y具有线性相关性的变量进行降维处理,但
只能表示二者之间不存在线性相关性,不能确认其之间没有非线性相关性。故对于附件一中325个样本数据中的操作变量并不适用。
4.3 随机森林(Random Forests)
随机森林[[i]][[ii]]对于回归和分类问题有很好的效果,随机森林还有一个重要特征:它能够计算单个特征变量在整个回归或分类过程中的的重要性指标(Variable Importance Measure),本文利用随机森林的这一特性对附件一中的354个操作变量进行特征提取,筛选出重要性指标最大的10个操作变量作为新特征。
记VIM为操作变量的重要性指标,本文选择基尼指数(Gini importance)作为354个操作变量的VIM值。作者在[[iii]]中计算传感器间的Gini importance作为传感器的贡献度量,从而实现后续对传感器优化的工作。本文利用sklearn构建随机森林的所有决策树中,输入均为354个操作变量,每个决策树对各个操作变量的Gini importance 进行计算,并根据各个操作变量的Gini importance从大到小进行排列。本文取354个操作变量中,Gini importance最大的前10个作为主要特征操作变量。特征选择结果如下表 4-1所示:
表4-1
| 操作变量名称 | VIM/Gini importance |
| 加热炉主火嘴瓦斯入口压力 | 0.030 |
| D101原料缓冲罐压力 | 0.029 |
| P-101B入口过滤器差压 | 0.026 |
| 精制汽油出装置硫含量 | 0.019 |
| 精制汽油出装置温度 | 0.017 |
| 非净化风进装置压力 | 0.0164 |
| E-101D壳程出口管温度 | 0.0162 |
| 稳定塔下部温度 | 0.016 |
| D-125液位 | 0.015 |
| K-103A进气温度 | 0.014 |
上述10个操作变量和7个原料性质(原料性质取了全部,未列出具体名称),共17个特征值作为自变量输入辛烷值损失模型的输入。
4.4 自回归滑动平均模型(ARMA)
ARMA模型曾广泛应用于时间序列的分析和预测,其中,ARMA的本质是利用输入的历史数据作为建模基础,基于其公式计算出未来时刻的最大可能发生的值。在此过程中,输入的时间序列是一组随时刻递进排列的数据元组,排除其时间序列的背景,其序列的本质可以视为一组具有隐含特性的特征向量,即一组可以唯一代表某一类特征的序列,并具有该类特征的全部属性。所以ARMA建模中的参数计算部分可以视为一种特殊的特征提取,将具备特征属性的大量数据序列,以参数向量的形式映射到欧氏空间中。基于此分析,我们尝试利用ARMA模型来捕获每个操作位的显式和隐式特征属性,每个特征都可由一个唯一的参数向量代表,且该向量具备了该特征的序列中的隐含属性,并将显式和隐式特征属性均体现在了参数向量中。另外,由于本题中的众多特征各具自身的单位,所以若要对比其与目标对象的影响大小,需要对数据进行归一化处理。而ARMA建模可以在参数计算的同时完成归一化。在建模过程中,可根据具体序列的特性定阶,而阶数则也是模型参数个数。特别的,不同序列的参数是各自唯一的。利用ARMA,可将序列映射到欧氏空间中,并可由其对应的向量唯一确定。
图神经网络是一种适用于多实体,且实体间具有一定影响的可构成网络模型的问题。为了在后续步骤中提供尽可能多的方法接口,我们在此处引入了图神经网络模型,并以图网络的形式对问题建模。本问题目的在于寻找354个可变操作位中,对RON损失影响最大的前n个操作位,其中各个操作位间具有不同程度的联系和影响,每个操作位可视为一个节点,而操作位间的影响可经过归一化后视为节点间边的权重。依据以上,可将全部样本建模为354+1(354为可操作变量,1为目标对象)个节点的完全无向加权图,共325帧。图模型网络示意图如下图 4‑1所示:
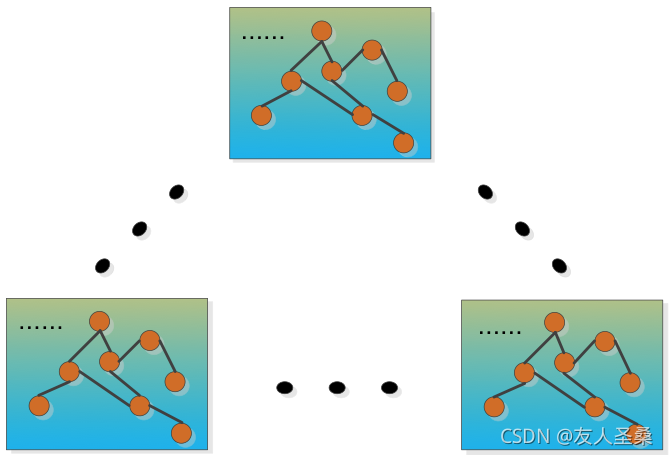
图4-1 图模型网络
利用以上特性,可将多个特征对目标对象的影响程度分析并提取主要特征的问题,转换成对一个维数为(355, 325)的图中多个节点的参数向量间影响因子的分析并寻找影响程度较大节点的问题。
在此问题中,我们将对各个节点进行图建模,并利用ARMA对各个节点进行参数向量求取,最后利用参数向量分析出各个节点对目标对象的影响程度。我们设计了算法1来实现该处细节:
算法1如下所示:

此处,在进行ARMA建模前还需对原始数据进行判别和整定,对于ARMA建模,需要进行数据平稳化处理,目的在于剔除掉序列中的趋势项。在此问题中,各个操作位的特征向量均是按照时间序列排成的,所以可能在实际工厂的操作中,会有时间趋势隐藏在操作位的变化中。即,该处的各个序列具有时间结构,所以对于具有时间结构的序列,进行趋势项分析和剔除是合理的。
完成数据平稳性检测和处理后,即是对节点进行ARMA建模。此处我们的阶数设置为ARMA(5,0)。确定阶数,即可得到对应数目的参数,并构建参数向量。此处省略公式。
最后,根据计算结果,距离目标对象参数向量欧氏距离越近的,影响因子越小,表示对目标对象(产品的RON)影响程度越高。依照此规则,我们确定了10个操作位,各个操作位与其对应的影响因子。特征选择结果如下表 4-2所示:
表4-2
| 操作变量名称 | 影响因子 |
| S_ZORB AT-0005 | 1.545 |
| 进装置原料硫含量 | 2.098 |
| D107转剂线压差 | 2.126 |
| 精制汽油出装置流量 | 2.793 |
| R-101底格栅上下压差 | 2.941 |
| 稳定塔底出口温度 | 3.120 |
| K-103B排气温度 | 3.151 |
| S_ZORB AT-0013 | 3.289 |
| 混氢点氢气流量 | 3.455 |
| 反吹气体聚集器/补充氢差压 | 4.113 |
5 问题三:建立辛烷值(RON)损失预测模型
5.1 问题分析
对目标进行建模,实际上也是一种回归或者映射的过程。针对本题目所给的场景,我们需要解决的问题即为,将若干个主要特征和因素,映射至成品汽油的辛烷值RON和硫含量。由问题二要求对数据进行降维,我们筛选出与输出指标相关程度最大的若干个特征作为模型输入,不仅大大缩减了运算复杂程度,也能够很好地将输入操作变量映射至实际汽油输出指标。
数据来源:附件一提供的325个样本数据,目标输出指标为:产品辛烷值(RON)和产品硫含量(μg/g)。输入参数为问题二得出的10个操作变量,加上样本的7个原料性质共17个。
问题要求:使用附件一中所提供的325个样本数据建立辛烷值(RON)损失预测模型,并对模型进行验证。
目标:利用附件一中样本的60%作为训练集对本文的模型进行训练,总样本的20%作为测试集,总样本的20%作为验证集,进行模型正确性验证和模型性能评估。
5.2 模型简析
问题三要求根据附件一所给数据集建立辛烷值(RON)损失预测模型,目前常用的预测模型建模方法主要有以下几类:
- 回归预测法。回归分析可以评估两个或多个变量之间的关系,常用的包括线性回归(Linear Regression),多项式回归[[i]](Polynomial Regression),岭回归(Ridge Regression)等等。可以有效解决具有线性相关性的问题,可以揭示若干个自变量对某个因变量的影响程度大小。
- 卡尔曼滤波[[ii]]。卡尔曼滤波是一种基于隐马尔可夫模型的最优线性估计算法,以最小均方误差作为估计的最佳准则,该算法模型主要操作可以分为两阶段,分别为预测和更新。在预测阶段,滤波器使用上一状态的估计,做出对当前状态的估计。继而在更新阶段,利用对当前状态的观测值优化在预测阶段获得的预测值,以获得一个更精确的新估计值。
- 组合预测模型。该类方法是用多种预测方法的组合,解决同一个问题。这类方法的优点在于,其可以利用各种预测方法所提供的信息,综合多种预测方法提供的信息,从而提高对目标问题的预测的精准度。
BP神经网络[[iii]]。BP神经网络是一种以误差逆向传播进行算法训练的多层前馈神经网络。其主要优点在于:非线性的映射能力、泛化能力和容错能力。该类方法可以储存大量输入与输出的映射关系,而无需给出具体的数学方程。在存在大量输入输出数据的时候,经过训练可以拟合出数据输入输出的非线性关系。故在处理这类复杂问题时,BP神经网络具有很大的优势。
5.3 模型结构
本文用BP(Back Propagation)神经网络对目标模型进行建模,BP网络为一种以误差逆向传播进行算法训练的多层前馈神经网络。根据问题二选择的主要特征数据:
第一层为输入层,由问题二对数据筛选的结果,输入层包括17个神经元,和一个截距项b1。其中前7个神经元的输入为原料性质相关参数,后10个神经元的输入为上文中所提及的10个操作变量。
第二层为隐含层,包括9个神经元,和一个截距项b2,并以输入层的每个神经元的输出作为输入。
第三层为输出层,根据问题三对建立辛烷值(RON)损失预测模型的要求,包含两个神经元,其输入均为隐含层9个神经元的输出,该层的输出分别为产品辛烷值(RNO)和产品硫含量(μg/g)。
由于BP神经网络每层的输出都是上一层输入的线性函数,若不使用激活函数,不管神经网络有多少层结构,其最终的输出都是输入的线性组合,故使用激活函数给BP神经网络引入非线性因素。本文设计的辛烷值(RON)损失预测模型的激活函数为ReLU[[i]](Rectified Linear Units)。
RELU函数作为激活函数有以下若干优点:
· 计算速度快:使用sigmoid函数计算反向传播求误差梯度时,计算量大,而使用ReLU函数的计算量要小很多,故在对神经网络进行训练时速度相对较快。
·应对梯度消失问题:对于一些深层的神经网络,采用sigmoid函数容易出现梯度小的问题,从而无法对网络完成训练。使用ReLU函数作为激活函数,由于其导数为1,计算梯度时不会导致梯度减小。
·缓解过拟合问题:使用ReLU函数作为激活函数,会使一部分神经元的输出为0,可以为整个网络引入稀疏性,减少网络中各个参数之间的相关性,缓解了过拟合现象的出现。
综上所述,我们对本BP神经网络的相关参数设置如下表 5-1所示:
表5-1 BP网络相关参数设置
| 网络层 | 节点数 | 激活函数 |
| Input layer | 17 | ReLU |
| Hidden layer | 9 | ReLU |
| Output layer | 2 | ReLU |
我们将在下文中分别将随机森林和ARMA模型对操作变量进行选择的结果,作为BP神经网络的输入,并对其进行相关分析。
5.4 损失函数
本文对模型损失函数的设置为总误差(square error),其值为误差平方和的1/2。针对问题三的模型建立过程中,本文中的BP神经网络是一种以误差逆向传播进行算法训练的多层前馈神经网络,采用梯度下降法对每一层神经元的参数进行更新修正。
5.5 模型评估
本小节分别利用问题二中两种特征选择方法(随机森林和ARMA)的输出结果,作为预测模型的输入,并对这两种方案进行整体模型评估对比。表1为两种特征选择方法的结果分别作为模型输入,其输出硫含量和辛烷值(RON)的指标对比。
此处对于原始数据集的划分为:训练集60%、验证集20%和测试集20%。以下展示实验结果为测试结果。由于原始数据集是按照时间序列排序的,为了排除工厂生产中存在阶段性的特性迟滞,防止引起局部过拟合,我们选择将数据集样本的排序顺序打乱,再进行划分。
产品辛烷值预测的准确率分别为:99.6%(随机森林+BP)、99.2%(ARMA+BP)
产品硫含量预测的准确率分别为:70.8%(随机森林+BP)、82.9%(ARMA+BP)
预测误差如下表 5-2所示:
表5-2 预测误差
| 产品硫含量,μg/g | |||
| RMSE | MAPE | MAE | |
| 随机森林+BP | 1.468 | 0.292 | 1.162 |
| ARMA+BP | 1.641 | 0.171 | 0.923 |
| 产品辛烷值RON | |||
| RMSE | MAPE | MAE | |
| 随机森林+BP | 0.437 | 0.004 | 0.357 |
| ARMA+BP | 0.910 | 0.008 | 0.694 |
6 问题四:主要变量操作方案的优化
6.1 问题分析
数据来源:附件一中全部样本数据,其中原料性质、待生吸附剂、再生吸附剂的性质保持不变。
问题要求:在保证产品硫含量不大于5μg/g的前提下,降低样本辛烷值RON损失大于30%,并得出对应的各个操作变量的优化结果。
目标:降低辛烷值RON损失值50%,并输出各个操作变量的优化结果。
本问题要求利用问题三中训练所得模型进行参数优化。整体来看,全部所选主要变量与目标变量间为非线性关系,对于非线性变量组间的多目标优化问题,遗传算法及其相关变种是应用较广泛的优化算法。
但对于本问题中的数据情况和可调步长要求,基于上述的问题分析,我们认为,也可用更简单、更符合题目要求、且计算资源需求量较小的方法来实现优化。
6.2 优化方案
根据题目要求,要以各个样本的当前样本数据集为基础,以操作变量信息作为操作标准,针对模型输出(产品硫含量、产品辛烷值)进行操作位变量优化。为了更贴近现实的工业生产,我们选取样本数据集的操作位参数为初始参数,并根据操作变量信息确定每个操作位的数值调整步长,因此,每个操作变量全部符合要求的可调值均为确定值,且均可枚举。另外,在问题二中,我们寻找出的变量均为对目标变量重要性较高的。且按照重要性由大到小,将全部可调变量排序。
依据以上特性,我们选择步进参数优化的方法,即从重要性最高的可调操作变量开始,逐个组成测试样本,遍历全部枚举对象,寻找最优解组合。此处需要说明,并不是遍历每个变量的全部取值间的排列组合,而是从重要性最高的变量开始,基于控制变量的思想,依次确定最优取值。此方法的优点在于计算量少,网络结构简单。由于所选的主要变量在实际的生产中并不是与其他变量相互独立的,所以在优化过程中应当一定程度上考虑变量间的相互影响,在此处可利用图神经网络中的邻接矩阵作为滤波器,输入特征矩阵来进行优化,但由于时间和计算资源有限,本方案基于控制变量的思想选择了更利于实现的逐个变量调整的方法。虽然无法最大程度上模拟实际生产,但由于我们的参数调整是从重要性最强的参量开始,且基于显示数据集进行数值调整,可以一定程度上避免可变参量间的相关影响,且相对于参量的完全随机初始化,更贴近生产中的实际操作。
- 依据问题二中的方法,确定输入的可变主要操作变量和不可变原料性质变量。提取优化参数的初始值,并按照变量操作信息的要求枚举出全部的可调参数值;
- 将全部参数组合依次代入模型,求出输出:产品硫含量、产品RON;
- 利用生成的产品RON和作为输入不可变量之一的原材料RON进行RON损失分析,通过比对筛选得出最优操作位参数组合。
6.3 优化结果及分析
结合问题五要求,先以编号为133的样本为例,描述优化结果。所选取的操作位名称可见问题二中所列结果。优化目标是维持产品硫含量不大于5μg/g,并使产品RON的损失降幅超过30%。对于133号样本,数据集中给出初始值的RON损失是1.3,可优化降幅空间较大,根据题目要求,只要优化后的可变参量可使RON损失小于0.9,即符合要求。
在前面的问题中,我们使用了两种方法进行特征提取,产生的结果也是不同的,所以此处也分别依照两组结果进行优化。在我们的两种方法中,损失降幅趋势均是呈非线性增长的,最终趋于平稳,RON损失均维持在0.6左右,特征提取使用ARMA+BP方法的优化结果比随机森林+BP的高2%。相对于原始数据,损失降幅均维持在60%左右,ARMA+BP的提取特征优化结果约为65.88%,随机森林+BP的提取特征优化结果约为63.21%。具体的图表将在问题五中进行可视化。并且,将会在问题五中进行更详细的解释。
从此实验结果来看,我们的方法可以达到题目要求的降幅大于30%的标准。
我们也针对全部样本进行了优化实验,由于325个样本中,部分样本的RON损失已经小于1,可优化空间较小,导致了整体的平均优化结果有所降低。在维持产品硫含量低于5μg/g的基础上,最后可实现的最优的RON损失降幅为53.42%(随机森林+BP)和54.01%(ARMA+BP)。
7 模型的可视化展示(略)
8 模型评价
8.1 模型优点
- 特征选择:使用RF对样本操作变量进行特征筛选,其本质是计算不同操作变量变化时对输出造成影响的大小,对输出影响大的操作变量为该问题模型的主要特征。利用随机森林进行特征选择得出的结果更具代表性,与目标输出指标(产品硫含量和产品辛烷值RON)更具相关性。将用于时间序列分析的ARMA对样本操作变量进行特征筛选是一个新的尝试,本文讨论并用实验证明了方法的可行性与合理性,利用ARMA模型来捕获每个操作位的显式和隐式特征属性,并将显式和隐式特征属性均体现在了参数向量中。故在操作变量筛选中,可以考虑到变量更多的特征。
综合上述两种特征选择方法能够从不同角度对主要操作变量进行调节操作,从而对产品辛烷值含量进行优化。最终的性能显示我们的两个方法均达到题目要求。
- 模型建立:本文根据样本数据特点选择BP神经网络作为预测模型的网络构架,其具有计算速度快,便于理解和实现等特点,其非线性的映射能力、泛化能力和容错能力强,在处理该类型样本数据中有很大优势。
- 参数优化:优化方法便利,直接利用问题三的模型,无需重构,减小了计算量和工作量,同时保证了一定的合理性和可行性,相比对初始值进行较复杂处理的其他算法更贴近工厂的实际生产情况。并可以达到很好的优化效果。
8.2 模型确定
- 特征选择:有限的方法限制了方法的对比与交叉验证。由于时间限制,我们只完成了图结构的建模,未能对数据进行图神经网络的训练,所以在特征降维阶段未能利用更有效的图分类方法进行特征提取,无法更全面的考虑节点的隐含特征,会导致提取的特征与真正的主要变量存在差异。
- 模型建立:该模型对主要操作变量之外的变量进行了理想化处理,这些变量在实际过程中可能存在一些不可忽视的波动,或者是与主要操作变量变化相关性强的影响等,这些可能会对模型的训练产生较大影响。为了应对这些因素,还需要进行更加细致的讨论。 另外,预测的结果在某些相对其他节点波动较大的节点存在一定程度的过拟合问题。需要进一步利用样本数据特性,或利用更大数量的数据集来进行训练。基于已完成的图结构建模,应当在此处利用更契合多节点非线性数据的图学习方法训练模型(滤波器)[[i]]。
- 参数优化:利用辛烷值损失预测模型对主要操作方案的优化,其过程难以真正模拟工业加工过程,仍需要在实际汽油精制过程中进行对应操作验证。部分参数的部分取值产生了输出异常,这应当是问题三中训练结果的泛化能力不足导致。针对优化,应当基于现有要求,利用神经网络重构模型,在第三问的结果基础上,增加更有效便捷的操作位参数调整训练。
[[i]] Z. Kang, C. Peng, Q. Cheng, and X. Liu eta, "Structured graph learning for clustering and semi-supervised classification", Pattern Recognition, 2020, 110, 107627.
[[i]] K. Tachibana and K. Otsuka, "Wind Prediction Performance of Complex Neural Network with ReLU Activation Function," 2018 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Nara, 2018, pp. 1029-1034.
[[i]] P. Gómez-Pérez, M. Crego-García and I. Cuiñas, "Modeling vegetation attenuation patterns: A comparison between polynomial regressions and artificial neural networks," 2016 IEEE International Symposium on Antennas and Propagation (APSURSI), Fajardo, 2016, pp. 2061-2062.
[[ii]] P. J. Hargrave, "A tutorial introduction to Kalman filtering," IEE Colloquium on Kalman Filters: Introduction, Applications and Future Developments, London, UK, 1989, pp. 1/1-1/6.
[[iii]] Z. Caihong, W. Zengyuan and L. Chang, "A Study on Quality Prediction for Smart Manufacturing Based on the Optimized BP-AdaBoost Model," 2019 IEEE International Conference on Smart Manufacturing, Industrial & Logistics Engineering (SMILE), Hangzhou, China, 2019, pp. 1-3.
[[i]] L. Breiman, "Random Forest", Machine Learning, 45(1), 5-32, 2001
[[ii]] P. Geurts, D. Ernst., and L. Wehenkel, " Extremely randomized trees", Machine Learning, 63(1), 3-42, 2006.
[[iii]] G. Wei, J. Zhao, Z. Yu, Y. Feng, G. Li and X. Sun, "An Effective Gas Sensor Array Optimization Method Based on Random Forest*," 2018 IEEE SENSORS, New Delhi, 2018, pp. 1-4.
[[i]] Hongchuan Yu and M. Bennamoun, "1D-PCA, 2D-PCA to nD-PCA," 18th International Conference on Pattern Recognition (ICPR'06), Hong Kong, 2006, pp. 181-184.
[[ii]] F. Ye, Z. Shi and Z. Shi, "A Comparative Study of PCA, LDA and Kernel LDA for Image Classification," 2009 International Symposium on Ubiquitous Virtual Reality, Gwangju, 2009, pp. 51-54.
[[iii]] H. Rajaguru and S. Kumar Prabhakar, "Performance Analysis of Local Linear Embedding (LLE) and Hessian LLE with Hybrid ABC-PSO for Epilepsy Classification from EEG signals," 2018 International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, 2018, pp. 1084-1088.
[[iv]] M. Peng, Z. WeiDong, L. Xiang and N. Junke, "Correlation Power Analysis for SM4 Based on ISOMAP," 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 2020, pp. 1165-1168.
[[v]] N. Pezzotti, B. P. F. Lelieveldt, L. v. d. Maaten, T. Höllt, E. Eisemann and A. Vilanova, "Approximated and User Steerable tSNE for Progressive Visual Analytics," in IEEE Transactions on Visualization and Computer Graphics, vol. 23, no. 7, pp. 1739-1752, 1 July 2017.
[[vi]] W. Teng, L. Cheng and K. Zhao, "Application of kernel principal component and Pearson correlation coefficient in prediction of mine pressure failure," 2017 Chinese Automation Congress (CAC), Jinan, 2017, pp. 5704-5708.
[[vii]] Robin Genuer, Jean-Michel Poggi, Christine Tuleau-Malot. "Variable selection using Random Forests. " Pattern Recognition Letters, Elsevier, 2010, 31 (14), pp.2225-2236. hal-00755489





















 2173
2173

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








