2018石中大集训总结

                        803测试总结———谢鹏宇

四道题目：

课程表(lesson)

相邻(adjacent)

兽皮 (skin)

汉诺塔(hano)

课程表(lesson)

问题描述：

今天是 Vasya  第一天来到初中。第一堂课，老师就把这一周的 n 节课和它们的时间都写在了黑板上。热爱学习的 Vasya 想要制作一张课程表， Vasya 想请你帮帮它，绘制一张漂亮的课程表吧。

输入格式  lesson.in ：

第一行输入 1<=n<=12 ，表示 vasya 一周要上的课。每节课的信息用两行来描述，第一行为课程名，每课程的名字由至多 5 个单词组成，单词之间仅由一个空格隔开，且单词长度在 1 到 10 之间。第二行由一个单词和一个数字给出，给出上课时间，表示这节课在星期几的第几节课上。因为 Vasya 上的是全国最著名的中学，他们只在 Tuesday , Thursday  和 Saturday 上课，并且每天的只有 4 节课。输入保证不存在同一个课时有两节课

输出格式  lesson.out ：

输出一个 4*3 的时间表 . 每一列从左到右表示三个工作日：第一列是 Tuesday  ，第二列是 Thursday,  第三列是 Saturday. 而每一行对应每天那 4 节课。每一列的列宽都是 10 个字符，而每一行的行高等于该行格子中最高的格子。如果该行所有课为空，那么行高为 1. 对于每个格子，如果一些单词不能完整地写入该行剩余的空间，那么这个单词就应当另起一行，并且要求左对齐。表格框使用“ -”(ASCII 45) ，“ +”(ASCII43) ，“ |”(ASCII 124) 绘制

总结：这道题目就是纯模拟，模拟的方法有很多，但是重点还是要预先处理出这一节课最多有几行，然后绘制表的时候，如果哪天的同样时间达到不了就可以绘制空格。还有一个重点就是处理一串名字，对他进行分行，哪些加起来达到10，哪些没有，哪些要重新换行，哪些不用，处理的时候有点麻烦。

相邻(adjacent)

问题描述：

Allen 正在举办一场晚会，他邀请了他的 n 个朋友和前来参加。但是他的 n 个朋友都把自己的女朋友带过来参加晚会了。在晚会结束的时候 Allen 把这 2n 个人随机打乱来照一张合影，但是他的朋们非常不满，因为他们不敢在照相的时候让女朋友不在身边。所以 Allen 只得不断地交换相邻两个人的位置，使得每个朋友都和他的女朋友站在相邻的位置。可是人数实在是太多了， Allen 觉得有点不堪重负。你能帮帮他吗

输入格式  adjacent.in ：

第一行输入 n<=1e5 ， 表示朋友个数

第二行有 2n 个数，每个数都在 1~n 之间，并且每个数 x 只会出现 2 次，出现的位置 i ， j 表示第 x 个朋友和他的女朋友所在的位置

输出格式  adjacent.out ：

一个整数，表示最小的交换次数。

样例输入 1 ：

4

1 1 2 3 3 2 4 4

样例输出 1 ：

2

样例输入 2 ：

3

1 1 2 2 3 3

样例输出 2 ：

0

数据范围与约定：

对 50% 的数据有 1<=n<=100

对 100% 的数据有 1<=n<=100000

总结：这道题目其实很好想，一下子就能想出来，我们先把某个部分取出来看看。

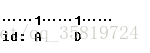（省略号是中间很多的数）我们现在要把下标为A和D的拼在一起，无论是下标A的1和右边的数不断交换到下标D-1，还是从下标D的1和左边的数不断交换到下标A+1，他们的交换次数是等价的。我们就看到底是D移动，还是A移动呢？如果D移动，那么AD区间的数会向右移，他们的另一半可能在下标A左边（这样就离另一半更远了），也可能在D下标的右边（这样就离另一半进了）同时A移动到D也是一样的。所以这样如果其中某个数离自己的另一半要远，那么它始终还要移到另一半那里，所以交换次数至少要多2。这样子去处理就很麻烦了，所以我们可以尝试一种贪心的选法，从左边第一个数开始，它的另一半一定在他的右边，然后把它右边的移动到它旁边卡住i+1这个位置，然后当你处理到下标j的时候，就能够一定保证从1到j-1的数都是处理好的（就是某个数都和自己的另一半挨在一起）这样子就保证了答案最小值（肯定是最小的，虽然证明不是很严谨）。我刚开始想到的，就是把每个数的右端点按出现顺序存放到一棵树状数组里面（图中的数字），存放的内容是它离他左端点的距离（也就是图中是数值）

看图，从左边第一位开始处理，答案加上数字1的数值（单点查询），然后当1要移动到它另一半的时候，右区间的243都会离他们的另一半要近一步，所以对数字i+1到n进行区间修改后面数字234对应的数字333就要变成222，以此类推找到最后面，（单点查询区间修改就用差分）。输出答案即可。刚开始这样的做法，自己测了几个数据都对了，但是后面我发现这种做法是错误的。举个反例：

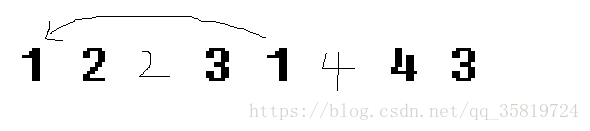把原数据的2和4 交换一下位置，当处理到1的时候，4和4之间本来就是隔着0，但是1后面的右端点储存的数值都要-1，那么它们的距离就变成了-1，所以这样就会导致错误呀。但是只是实现的方法错了，不代表之前推出来的一大堆东西错了，换一种实现方法试试。其实仔细想想会发现，移动次数就是逆序对的个数，为什么这么说呢，把每个数按先后出现的顺序，把它和它另一半标为同一的cur，然后cur++，然后按照他的大小求逆序对个数就可以了。

兽皮 (skin)

题目描述：

经过三百多天的炮制，巫婆终于把手头的 n 张兽皮制成了药材。这可真是个令人兴奋的消息，可是坏消息同样接踵而至——这些兽皮太脆弱了。经过多次尝试，巫婆找到了一个绝妙的保存方法方法。巫婆拿出自己第一版的《算法导论》，对它施以魔法之后，将兽皮夹在书页中，这样，这些药材就不会那么快变质了。然而巫婆发现兽皮会对纸页进行渗透，对于第 i 张兽皮，它会渗透 ai 张纸，尽管这不会伤害 i 本身，但是，如果某张皮在 [i-ai,i+ai] 的书页间， j 就

会被 i 所渗透而变质。同时巫婆不想使这本书太难看，所以每张兽皮 i 距离封面封底的距离也不少于 ai由于经常学习算法导论，巫婆的书页所剩无几。他想知道最少要多少页纸可以完好地保存这 n 张兽皮。

输入格式  (skin.in) ：

共两行，第一行 n 表示个数。第二行 n 个整数数 a1...an 表示每张兽皮的渗透距离

输出格式  (skin.out) ：

一个整数，表示最少所需书页

样例输入：

3

5 10 3

样例输出 :

28

数据范围 及 约束：

对 30% 的数据 1<=n<=100

对 100% 的数据

1<=n<=10^5

1<=ai<=10^5

总结：可以说这道题目是一道水题吧。首先我们想，它最少所需的书页，就意味着你要尽可能地覆盖的多的兽皮的长度（这里默认兽皮长度为它渗透长度）。首先，最长的兽皮肯定是不能被别人覆盖的，其它兽皮只能尽可能地覆盖在别人的兽皮的另一半下，只要这一张兽皮放在渗透长度大于等于它的兽皮下就可以让它一半被覆盖，然后可以简单证明，除了最长的那张兽皮，其它都会被别的兽皮覆盖一半，所以答案就是最长的兽皮*2+其它的兽皮渗透长度，如果最长的有多张，只选一张*2+剩下的所有的。

汉诺塔(hano)

题目描述：

汉诺塔游戏最初是由法国数学家 Edouard Lucas 在 19 世纪后半叶提出。现在的汉诺塔游戏一般都只有由三根柱子，并且有 n 个大小不同，厚度一致的圆盘。初始状态所有的圆盘都在 A 柱上，游戏的目标是把圆盘从下面开始按大小顺序重新摆放在另一根柱子 C 上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。有一天你发现一个初中小朋友在玩汉诺塔，刚刚学习完汉诺塔递归算法的你发现他手头上的局面似乎常混乱，你也搞不清下一步该怎么走了。。。于是你把他手头的柱和塔夺了过来，打算一步步还原到初始状态重新玩过。在问题来了，你究竟要走多少步才能回到初始状态呢？

输入描述 (hano.in) ：

第一行 n 表示圆盘个数，

第二行一个字符串 s[1...n] ， s[i]==A 或 B 或 C ，表示第 i 个圆盘现在哪根柱子上。

输出描述 (hano.out) ：

一个整数，表示最少所需步数。

样例输入 1 ：

1

A

样例输出 1 ：

0

样例输入 2 ：

4

BBBB

样例输出 2 ：

15

样例输入 3 ：

7

BCCBABC

样例输出 3 ：

95

数据范围与约束 :

对 20% 的数据 1<=n<=10

对 100% 的数据 1<=n<=50

总结：我们拿样例输入3来说话吧

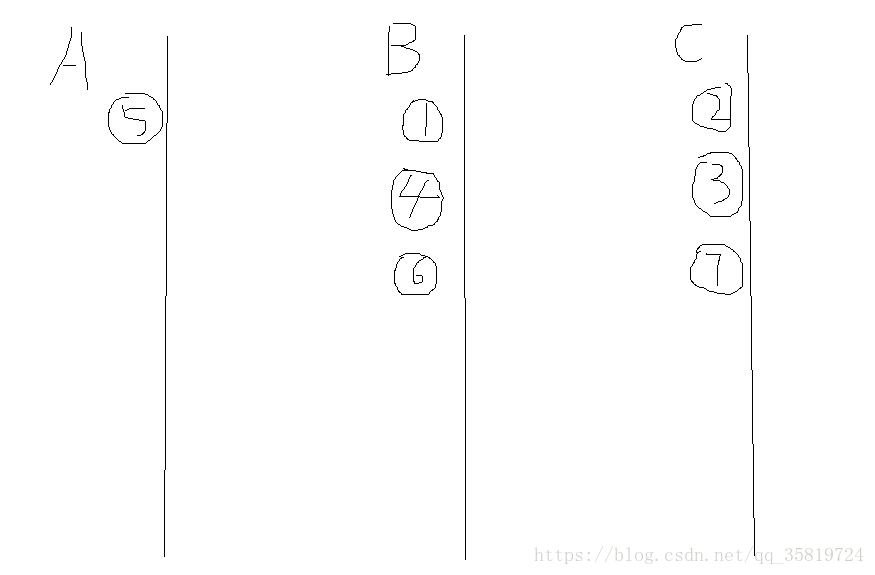我们的最终任务是把7个盘子全部移到A上面，我们用F（i，j）表示把第1到i个盘子移动到第j个棍子的最少移动步数。看图中，先得到（7，A）吧，7现在在C柱上，如果要移动到A且作为最下面的盘子，那么A柱和C柱都是空的并且7在C柱上，所以我们现在的子问题是F（6，B）把剩下的所有的盘子都移动到B上面，然而6已经在B柱上了，我们就考虑F（5，B）把1到5的盘子都移动到B上，也就是C柱要为空，所以1到4的盘子都要在C柱上，所以又转化成了F（4，C）然后按照这种方法递推下去，最后当到达1个盘子的时候如果这个盘子本来就在这根柱子上就返回0，否则返回1。

#include<iostream>

#include<cstdio>

#include<cstring>

using namespace std;

int n,num[15000];

long long count[150000];

string a;

 

long long DFS(int id,int target)

{

    if(id==1)

    {

       if(target==num[id]) return 0;

       else return 1;

    }

    if(num[id]==target) return DFS(id-1,target);

    bool w[4];

    w[0]=w[1]=w[2]=false;

    w[target]=1;

    w[num[id]]=1;

    for(int i=0;i<3;i++)

       if(!w[i])

           return DFS(id-1,i)+count[id-1];//这个count就是前id-1个盘子要移动到想去的地方的方案（这个应该初学hanoi的时候就有研究过步骤数是2^n-1），其实这里是神略了原来应该这样子写   return DFS(id-1,i)+（count[id-1]-1）+1; （count[id-1]-1）这个是id-1个盘子的步骤数，然后1是第id个盘子移动到想要到达的目标的步骤就是一步，然后抵消了。

}

 

int main()

{

    freopen("hano.in","r",stdin);

    freopen("hano.out","w",stdout);

    cin>>n;

    cin>>a;

    for(int i=0;i<a.size();i++)

       num[i+1]=a[i]-'A';

    count[0]=1;

    for(int i=1;i<=n;i++)

       count[i]=count[i-1]*2;

    cout<<DFS(n,0);

    return 0;

}