浅谈CDQ分治

                                                入门CDQ分治         

    首先介绍这个名字，是陈丹琦（CDQ）创造的分治方法，主要部分应该是降维思想。先给道例题吧。归并排序都知道吧，先分后合，其实就是分治的思想，对于某个区间X他的左子区间L,和右子区间R，如果都是有序的，那么我们就开始从左区间第一个和右区间第一个比较，哪个大哪个取出来（当然Cmpare的方式自己可以定义），最后这个区间就是一个有序的区间了。程序大概是这样写的。(伪代码)

void mergesort(int l,int r)
{
    int i=l,j=(l+r)/2+1,mid=(l+r)/2,cur=l;

    while(i<=mid&&j<=r)
    {
        if(a[i]<a[j]) temp[cur++]=a[i++];
        else temp[cur++]=a[j++];
    }

    while(i<=mid) temp[cur++]=a[i++];
    while(j<=r) temp[cur++]=a[j++];

    for(int i=l;i<=r;i++)
        a[i]=temp[i];

    return;
}


void merge(int l,int r)
{

    if(l==r) return;
    int mid=(l+r)/2;

    merge(l,mid);
    merge(mid+1,r);

    mergesort(l,r);

    return ;
}

merge函数就是一个一直在分治的函数，分治的格式也差不多是这样。但是有些情况下，我们会先分治左边，然后去更新右边的值然后再分治右边。。。

然后我们放例题吧。https://www.luogu.org/problemnew/show/P3374

虽然是树状数组的模板题，其实也可以用CDQ分治做。

首先我们要知道偏序是个是那么东西，对于一个序列(a,b)，有个序列（a1,b1）满足（a1<a,b1<b）那么就是一个偏序问题，其实不一定是这样的他可以（a1>a,b1<b）只要是个不等关系应该都可以叫做偏序，放在图上表示就是如果对于某个点在他的某个象限里有数，那么对应的偏序就是哪个象限怎么用这个序列去表示。。然后偏序有二维偏序，当然也有三维偏序，当然也有四维偏序。我们看看树状数组的模板题目，他其实暗含了一个偏序对吧，就是时间，因为他是按顺序加点，按顺序询问的，他的时间一定要按顺序来，所以这是一个二维偏序问题，（时间，位置）对于某个询问(ai,bi)我们就要看是否存在修改（aj,bj）满足（aj<ai,bj<=bi）也不就是个偏序吗。如果有满足的，那就会对这个询问照成影响对吧。我们想，插入的话就直接作为一个操作，放进去在某个点插入Val，如果询问的话，我们发现对于[l,r]区间我们只用处理他们的前缀和就可以了[l,r]=sum[r]-sum[l-1]；所以我们把询问变成两个操作，询问两个的前缀和。先看一下我的结构体吧。。。

struct ST{

	int x,val,sign,id;
	ST() {}
	ST(int X,int V,int S,int I)
	{
		x=X;val=V;sign=S,id=I;
	}
	bool operator < (const ST b) const
	{
		return x<b.x;
	}
}st[max_m*2],temp[max_m*2];

里面有构造函数，先别管这个。x是当前这个操作的位置（下标），Val就是这个操作的权值，给某个点加入多少,sign就是标记当前这个操作是否是查询，1表示是查询，0表示是插入，id是映射他在原来输入顺序的位置。所以我们输入的时候是这样的

	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)//刚开始的初始数列也当作插入操作处理
	{
		int a;
		scanf("%d",&a);
		st[++total]=ST(i,a,0,0);//四个变量表示，位置，权值，sign,id
	}
	
	for(int i=1;i<=m;i++)
	{
		int cmd,a,b;
		scanf("%d%d%d",&cmd,&a,&b);
		if(cmd==1)
		{
			st[++total]=ST(a,b,0,0);
		}
		else
		{
			turn++;
			st[++total]=ST(b,1,1,turn);//turn映射第几个询问
			st[++total]=ST(a-1,-1,1,turn);//这个权值为1和-1是有用的后面介绍
		}
	}

不懂这种奇奇怪怪用法的同学，上网搜一下构造学习一下吧。然后我们就要进入正题了，，，我们开始分治了，怎么分治呢，看好了。。。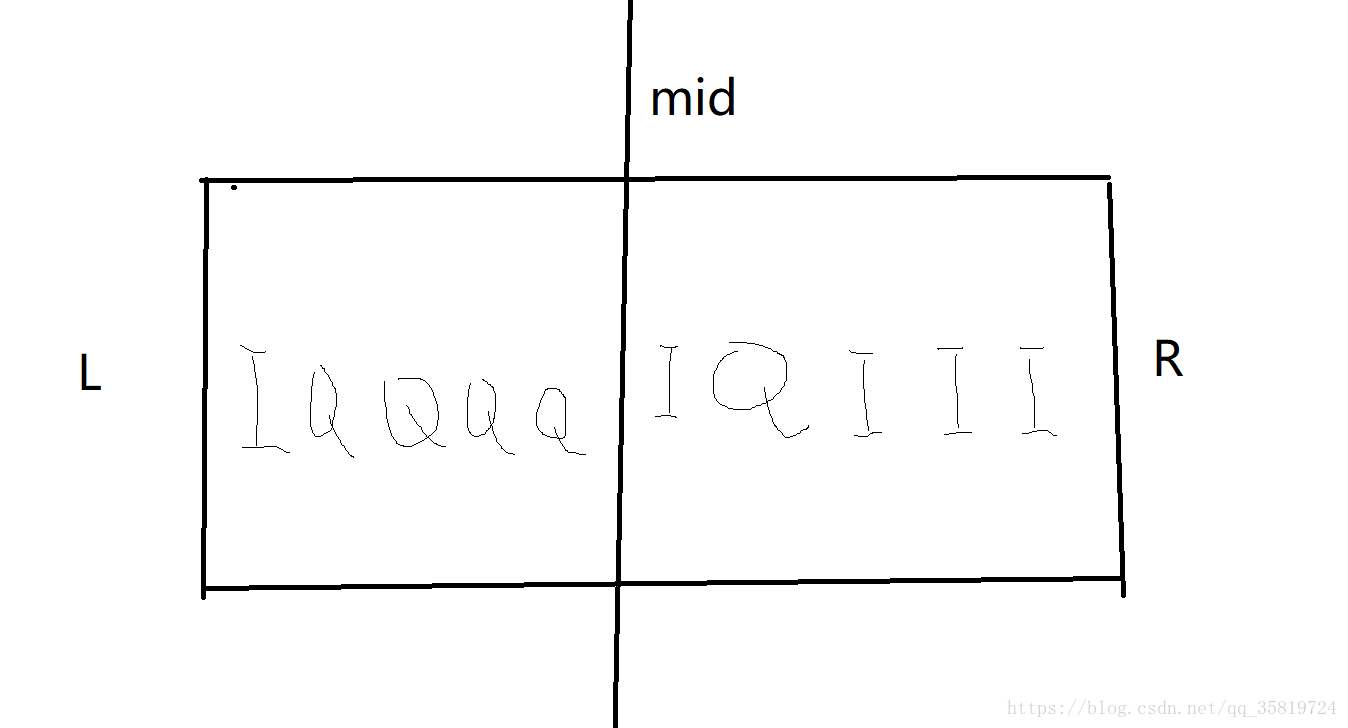看这个图吧，I是插入，Q是询问，左边区间的每一个操作的时间，一定比右边区间的每一个操作的时间短。如果L区间已经统计过答案了，R区间也统计过答案了，L区间怎么打乱对最后的答案都不会有影响。所以我们就搞一个扫描线，从左往右扫描一次就行了。代码如下

void CDQ(int l,int r)
{
	if(l==r) return;
	int mid=(l+r)/2;
	CDQ(l,mid);
	CDQ(mid+1,r);
	merge(l,mid);
	merge(mid+1,r);
	int i=l,cur=0;
	for(int j=mid+1;j<=r;j++)
		if(st[j].sign)看右边的区间，如果是个询问的话
		{
			while(st[i].x<=st[j].x&&i<=mid)//就从左边找在他前面的修改（前缀和肯定要看前面的啊）
			{
				if(!st[i].sign) cur+=st[i].val;//先把他们的值给加上	
				i++;
			}
			ans[st[j].id]+=cur*st[j].val;//之前讲到的询问的VAl终于有用了，仔细想想这个询问的答案不就是sum[r]-sum[l-1]吗，所以乘一个1或者-1就表示是+sum[r]还是-sum[l-1]了
		}
	
	return;
}

详细代码如下

#include<iostream>
#include<cstdio>
#include<algorithm>
#define max_m 5000005
using namespace std;

int n,m,turn=0,total=0,ans[max_m*2];

struct ST{

	int x,val,sign,id;
	ST() {}
	ST(int X,int V,int S,int I)
	{
		x=X;val=V;sign=S,id=I;
	}
	bool operator < (const ST b) const
	{
		return x<b.x;
	}
}st[max_m*2],temp[max_m*2];

void merge(int l,int r)
{
	int i=l,j=(l+r)/2+1,mid=(l+r)/2,cur=l; 
	while(i<=mid&&j<=r)
	{
		if(st[i]<st[j])
		{
			temp[cur]=st[i];
			cur++;
			i++;
		}
		else {
			temp[cur]=st[j];
			cur++;
			j++;
		}
	}
	while(i<=mid) 
	{
		temp[cur]=st[i];
		cur++;
		i++;
	}
	while(j<=r)
	{
		temp[cur]=st[j];
		j++;
		cur++;
	}
	for(int i=l;i<=r;i++)
		st[i]=temp[i];
	return;
}

void CDQ(int l,int r)
{
	if(l==r) return;
	int mid=(l+r)/2;
	CDQ(l,mid);
	CDQ(mid+1,r);
	merge(l,mid);
	merge(mid+1,r);
	int i=l,cur=0;
	for(int j=mid+1;j<=r;j++)
		if(st[j].sign)
		{
			while(st[i].x<=st[j].x&&i<=mid)
			{
				if(!st[i].sign) cur+=st[i].val;	
				i++;
			}
			ans[st[j].id]+=cur*st[j].val;
		}
	
	return;
}

int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		int a;
		scanf("%d",&a);
		st[++total]=ST(i,a,0,0);
	}
	
	for(int i=1;i<=m;i++)
	{
		int cmd,a,b;
		scanf("%d%d%d",&cmd,&a,&b);
		if(cmd==1)
		{
			st[++total]=ST(a,b,0,0);
		}
		else
		{
			turn++;
			st[++total]=ST(b,1,1,turn);
			st[++total]=ST(a-1,-1,1,turn);
		}
	}
	
	CDQ(1,total);
	
	for(int i=1;i<=turn;i++)
		printf("%d\n",ans[i]);
		
	return 0;
}

B P3810 【模板】三维偏序（陌上花开）

C P4390 [BOI2007]Mokia 摩基亚

你们可以去做做，这个是三维偏序，用排序降一维，用CDQ降一维，最后就用树状数组搞定。