YbtOJ NOIP2020 模拟赛 B 组 Day8 B.柱子堆放【数学】

最新推荐文章于 2021-09-26 18:36:48 发布

原创最新推荐文章于 2021-09-26 18:36:48 发布

· 140 阅读

0 ·

版权

数学专栏收录该内容

28 篇文章

订阅专栏

...

题目：
题意：
分析：
代码：

题目：

传送门

题意：

感 $j i o$ 数学几何题自己去康题面好了

分析：

对于两个圆心之间的距离，我们来康下图：
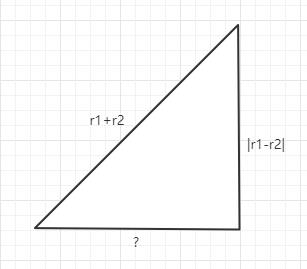
在这里插入图片描述
$?$ 就是我们需要求的圆心距离的了，用小学二年级的勾股定理轻松解决
接下来考虑答案怎么计算
我们最后的圆柱体一定是可以有两个圆柱体紧挨着，但它们下边的空隙能藏几个就不好说了
设 $f_i$ 表示第 $i$ 个圆柱体到左挡板的距离
我们先假设 $i, j$ 一定是紧挨的，那么由 $j$ 转移到 $i$ 就是 $f_i=f_j+\sqrt {(r_i+r_j)^2-(r_i-r_j)^2}$
可实际情况显然会出现中间的圆柱体将两者挤开，使得它们不能挨在一起，想一想，要满足一定能藏好之间的圆柱体，那一定会满足在答案中距离最大，因为最大的时候显然是藏得最少，也即是能保证藏好的情况
最后答案就为 $max\{f_i+r_i\}$

代码：

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define LL long long 
using namespace std;
inline LL read()
{
	LL s=0,f=1; char c=getchar();
	while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9') {s=s*10+c-'0';c=getchar();}
	return s*f;
}
double max(double x,double y) {return x>y?x:y;}
int r[1005]; double f[1005];
int main()
{
	freopen("column.in","r",stdin);
	freopen("column.out","w",stdout);
	int n=read();
	for(int i=1;i<=n;i++) r[i]=read();
	f[1]=r[1];
	for(int i=2;i<=n;i++)
	{
	  f[i]=r[i];
	  for(int j=1;j<i;j++) 
	    f[i]=max(f[i],f[j]+(double)sqrt((r[i]+r[j])*(r[i]+r[j])-(r[i]-r[j])*(r[i]-r[j])));  
	}
	double ans=0;
	for(int i=1;i<=n;i++) ans=max(ans,f[i]+r[i]);
	printf("%.3lf",ans);
	return 0;
}