BP神经网络细解——含代码，有详细说明，哈工大模式识别实验

我们以一个实验来说明整个流程，包括了数据生成，网络构建，网络训练，预测和最终验证。实验的要求如下：

---

一、实验计划

1.数据生成

采用np.random.multivariate_normal (mean, cov, size=None, check_valid=None, tol=None)方法，它用于生成多元正态分布矩阵。其中mean和cov为必要的传参而size，check_valid以及tol为可选参数。

2.网络结构定义，前向传播

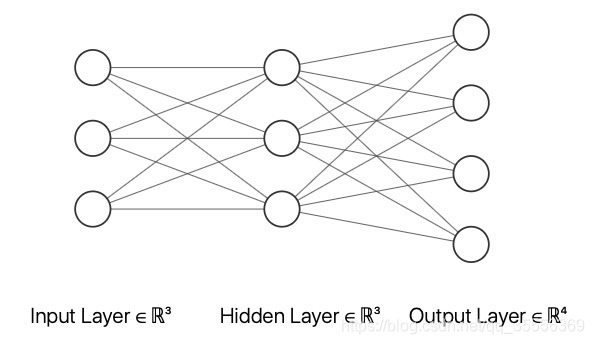
网络采用3-3-4型BP网，即输入层为3，隐藏层为3，输出层为4，含偏置项，隐藏层激活函数采用ReLu，输出层采用softmax，loss函数J(W)采用均方差，如下所示，其中tk是实际标签，zk为网络估计的结果，c为样本的类别数。

3-3-4 BP网的结构如下图所示。由于输入为三维样本点，因此输入层为3；由于需要分为四类，因此输出层为4。中间隐藏层节点数和层数可随意组合，本实验设为3个。

前向传播较为简单，规则如下。xj是输入样本，wkj是权重矩阵，wk0是偏置值。

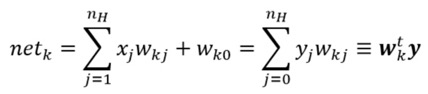
经过上式计算出输出后，经过激活函数得到如下结果。f为激活函数，本实验隐层采用ReLu，输出层采用softmax。

3.反向传播

该部分对于初学者是较难理解的部分，建议多花时间理解透彻，其实本质就是对loss函数求偏导，以达到降低loss就能优化网络的目的。偏导的求解过程读者可自行推导，对J(w)求导即可。最终得到权重的更新公式如下：

其中，wji是输入到隐藏层的权重，维度为3*3，wkj是隐藏层到输出的权重，维度为4*3。xi是输入样本，yj是隐藏层经过ReLu激活后的输出。det j和det k分别是隐层和输出层的敏感度。它们的定义如下，f'是softmax的偏导数。

4.预测

最后,经过softmax之后的输出,求其最大值所在的索引,将它作为预测的标签，具体规则是np.argmax(softmax(net k))。

---

二、实验过程

均方差的定义如下：

def mean_square(output, y):
    return np.sum((y - output) ** 2) / 2.0

softmax的定义如下：