1.极限定义的使用
不关心这点是否出问题
关心点是趋近过程中不能出问题
例题
2.利用夹逼定理
例题
lim|f(x)|=A(A!=0),不能推出limf(x)=A,如果A=0,则成立

3.四则运算法则
前提,极限得存在
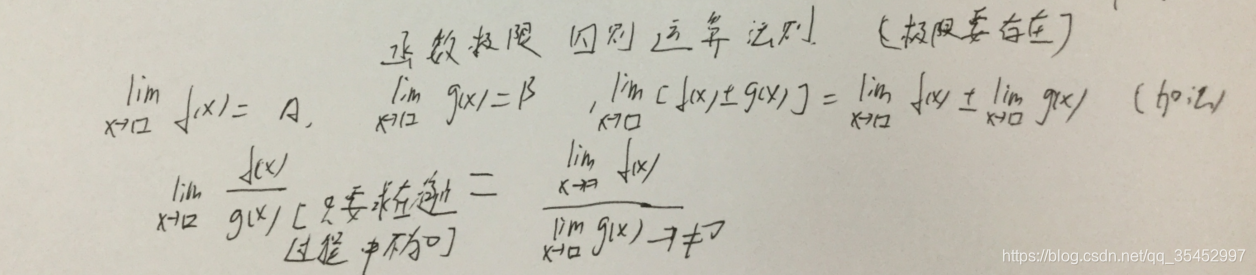
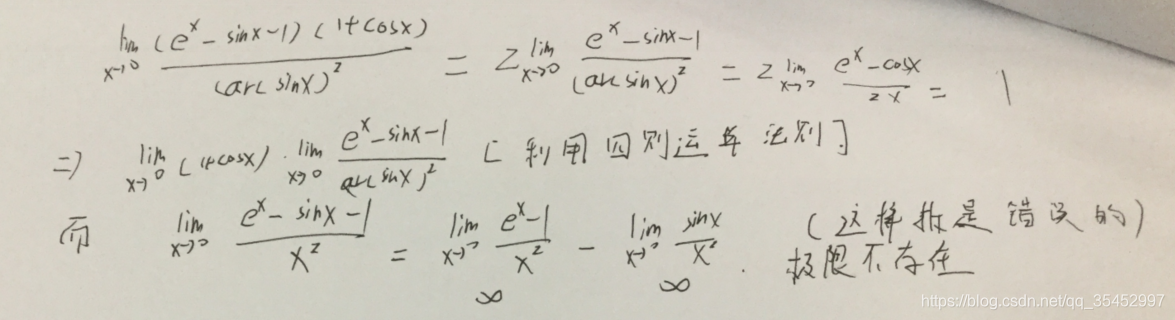
4.未定型
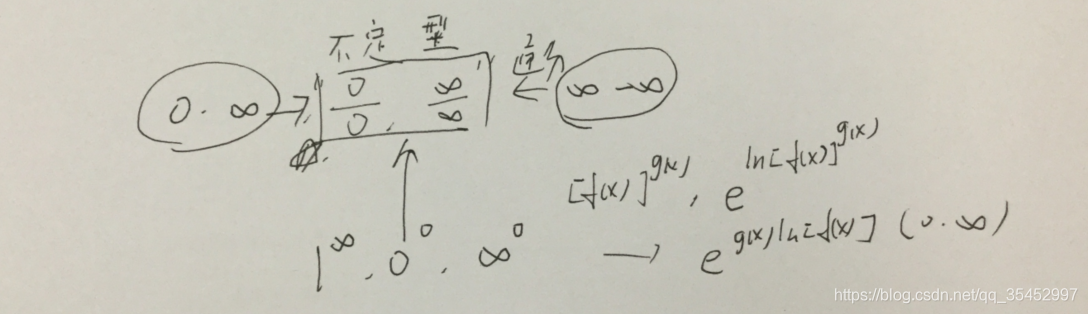
核心为0/0,无穷/无穷型
其余的,0*无穷,无穷-无穷,1^无穷,0^0,无穷^0,均可化为核心的两个
5.洛必达法则
如果结果为无界非无穷大,则洛必达失效
 本文详细探讨了函数极限的计算,包括极限定义的应用,夹逼定理的例题解析,四则运算法则的前提与应用,未定型极限的处理,特别是0/0和无穷/无穷型,以及洛必达法则的适用条件和泰勒公式的介绍。重点讲解了如何处理特殊形式的极限问题。
本文详细探讨了函数极限的计算,包括极限定义的应用,夹逼定理的例题解析,四则运算法则的前提与应用,未定型极限的处理,特别是0/0和无穷/无穷型,以及洛必达法则的适用条件和泰勒公式的介绍。重点讲解了如何处理特殊形式的极限问题。
1.极限定义的使用
不关心这点是否出问题
关心点是趋近过程中不能出问题
例题
2.利用夹逼定理
例题
lim|f(x)|=A(A!=0),不能推出limf(x)=A,如果A=0,则成立

3.四则运算法则
前提,极限得存在
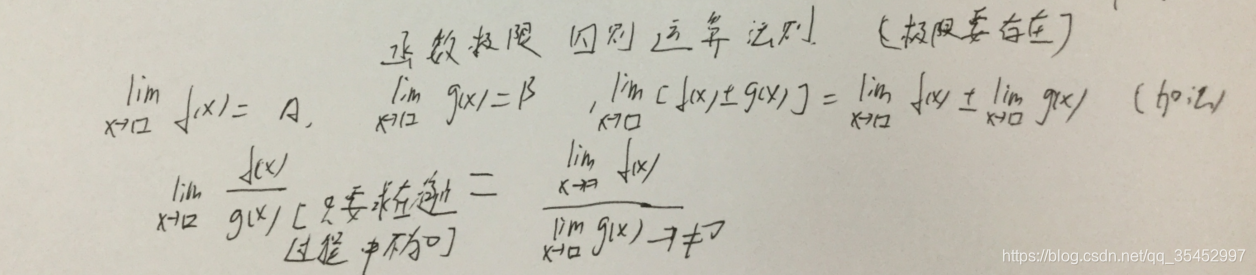
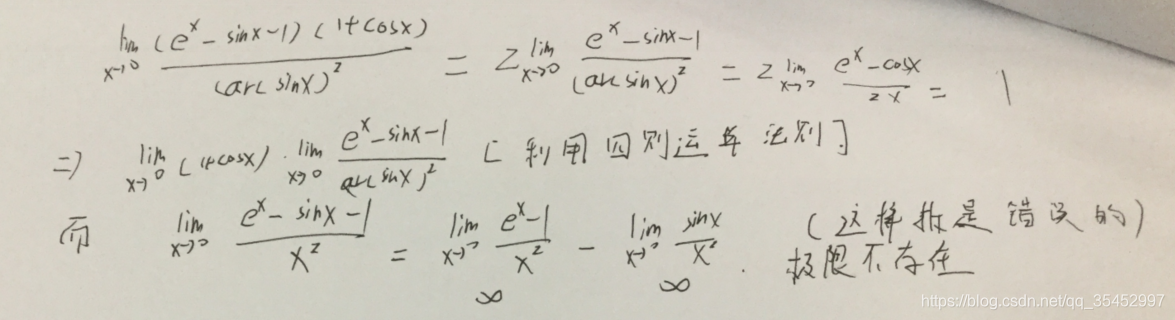
4.未定型
核心为0/0,无穷/无穷型
其余的,0*无穷,无穷-无穷,1^无穷,0^0,无穷^0,均可化为核心的两个

5.洛必达法则
如果结果为无界非无穷大,则洛必达失效
 5078
5078

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


