使用HTML Canvas绘制五角星(二)

上一次讲到利用五边形确定五角星五个顶点的位置（点击链接可查看），今天讲另外一种方式的实现，使用canvas的旋转rotate方法就可以轻松实现，MDN官网的例子也是这个方式，可以大概先讲下逻辑：每一次旋转π/5的角度，

旋转第一次：假设x轴有一个点的坐标是A1（20,0），旋转后某一个坐标A2(20*0.6, 0)， 连接该两点；

旋转第二次：A3（20,0）， 连接A2和A3；

旋转第三次：A4（20*0.6, 0）， 连接A3和A4；

旋转第四次：A5（20, 0）， 连接A4和A5；

以此类推，就是通过每一次旋转π/5的角度，连接长短不一（一长一短间隔）的两个点画线，如下图所示：

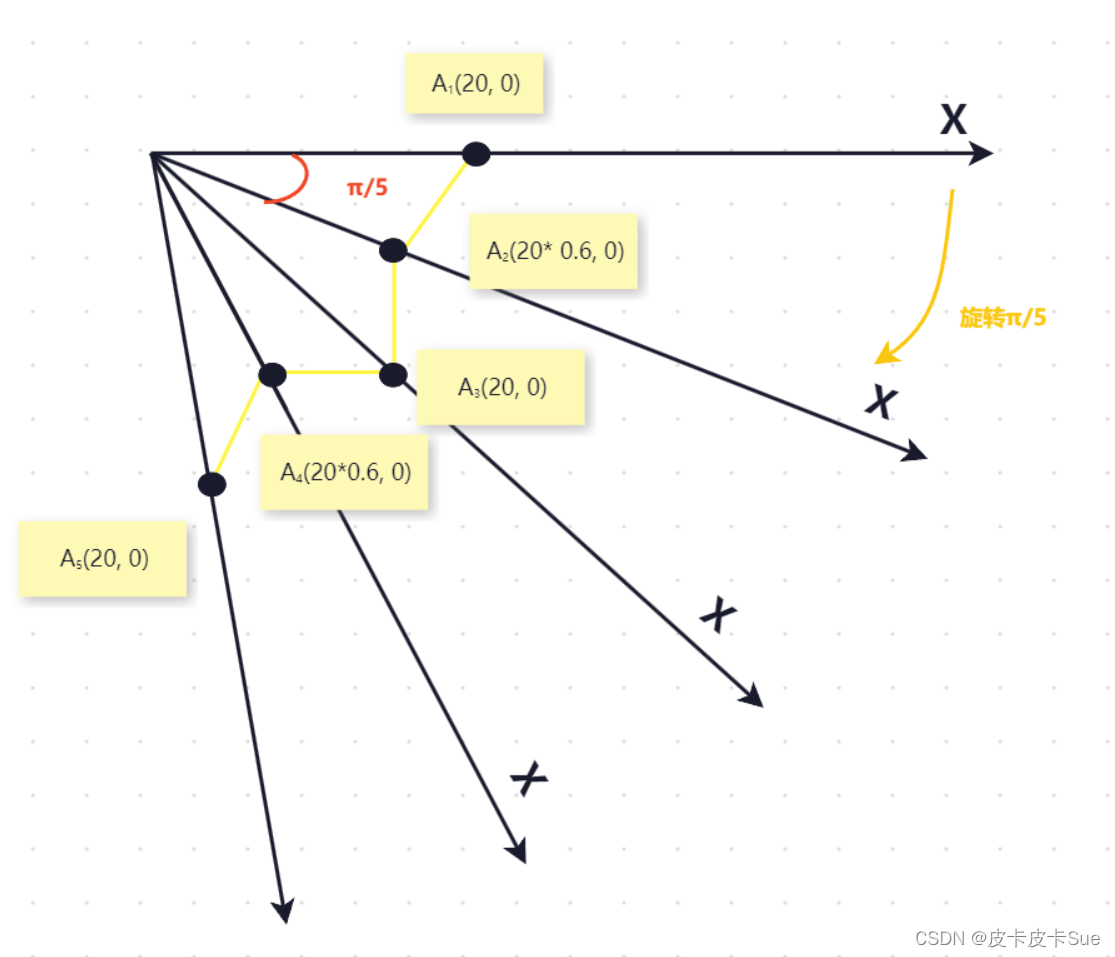
这样还不太看出来效果，看下实际的效果图：

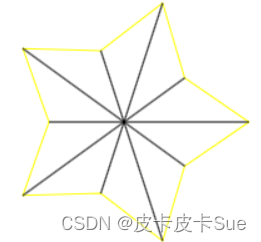
这样是不是就能理解了，是通过坐标轴的旋转来实现画五角星的（由此是不是打开思路了，那我是不是n角星也可以这样轻轻松松实现啦？那当然了啊，感兴趣的同学可以自己试试，就是旋转角度的差别）

主要代码实现：

// 绘制黄色五角星
context.translate(300,300);
context.save();
context.strokeStyle = 'rgb(255,255,0)';
context.beginPath();
//100为五角星外角距离中心的长度
context.moveTo(100, 0);
  for (var i = 0; i < 9; i++) {
    context.rotate(Math.PI / 5);
    if (i % 2 == 0) {
        //100*0.6为五角星内角角距离中心的长度
        context.lineTo(100*0.6, 0);
    } else {
        context.lineTo(100, 0);
    }
  }
  context.closePath();
  context.stroke();

  // 绘制中间黑色线部分
  context.restore();
  context.beginPath();
  context.moveTo(0, 0);
  context.lineTo(100, 0);
  context.stroke();
  for (var i = 0; i < 9; i++) {
    context.rotate(Math.PI / 5);
    context.beginPath();
    context.moveTo(0, 0);
    if (i % 2 == 0) {
        context.lineTo(100*0.6, 0);
    } else {
        context.lineTo(100, 0);
    }
    context.stroke();
  }

最后扩展：

可能会有同学问：内角距离中心点的0.6是这么来的，这个要看你五角星的要胖一点还是瘦一点啦，但不能超过0.8左右，超过就会变成五边形，甚至多边形，具体可以看图就知道了：

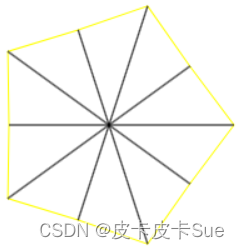
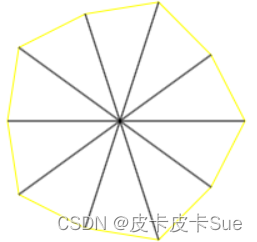
至于0.8左右怎么算出来的呢？留个小问题，感兴趣的同学可以研究下，或者评论留言~~