Group Consistent Similarity Learning via Deep CRF for Person Re-Identification
作者:Dapeng Chen, Dan Xu,Hongsheng Li等人 2018 CVPR oral
1. 摘要
大部分现有方法只考虑了局部约束的相似性学习,而本文中通过结合CRF和DNN还额外进行组相似性学习。训练时,在一个CRD框架中集成了多张图像的局部相似性和组相似性,在测试时结合多个尺度的局部相似性作为预测相似性。
2. 介绍
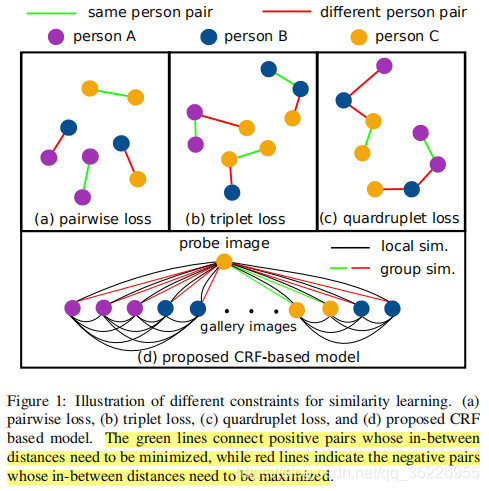
现有方法多进行图1a~c所示,但性能都很依赖于采样策略,导致次优解。
作者提出利用一个组的图像对复杂的图像2图像关系进行建模,一个组的图像由一张probe图像和一系列gallery图像组成,定义局部相似性和组相似性描述图像间关系,但前者是基于两张图像的,而后者是基于整组图像的。这两种相似性通过一个统一的图模型CRF建模,其中,局部相似点是已观察到的输入变量,而组相似点是要预测的输出变量。而优化组相似性可以反过来学习更一致的局部相似性度量和特性嵌入。此外,受益于图模型的灵活性和表征力,能够有效融合多尺度特征嵌入的不同种类的局部相似性,进行更准确的相似性估计。为了用DNN实现该模型,作者推导了近似推理来估计组相似性,并给出了均值场(mean-field)更新过程。包含了三个子网络,分别是:multi-scale feature embeddings (MFE), local similarity computation (LS) 和 group similarity estimation (GS),而值得注意的是仅在训练阶段进行组相似性估计,而在测试阶段通过对多尺度的局部相似性进行线性组合作为相似性预测,而线性组合的参数是通过CRF自适应学习的。
贡献:
- 结合CRF和DNN以学习更一致的多尺度相似性度量
- 端到端
- 有效
3. 方法
目录:
- 3.1----定义了图像组内的局部相似性和组相似性
- 3.2----在CRF中对它们联合建模
- 3.3----对于网络实现,采用了一种近似的组相似性估计推断
- 3.4----设计的三个子网络模块
- 3.5----整个网络
- 3.6----训练细节
3.1. 局部相似性和组相似性
DNN的训练数据通常是分bacth的,其中图像不仅参与了相同的前向和反向传播进行优化,而且还包含了丰富的图像间相关性。 本文以bacth的方式构造图像group,每个group中的图像数量是灵活变化的。
设OOO表示一个组中的所有图像,其中一个是probe图像IpI_pIp,而其余的是gallery图像,设为G=I1,I2,...,IGG={I_1,I_2,...,I_G}G=I1,I2,...,IG,本文定义tm,nt_{m,n}tm,n为局部相似性,表示一个组内的两张图像ImI_mIm和InI_nIn之间的相似性(不论probe和gallery),其仅与这两张图像的外观有关。另一方面,两幅图像之间的相似性也可以通过它们与其他图像的关系来推断。本文进一步定义了probe图像IpI_pIp和gallery集G中任一张图像IiI_iIi之间的组相似性yp,iy_{p,i}yp,i。yp,iy_{p,i}yp,i是利用整个图像组进行相似性估计。
局部相似性tm,nt_{m,n}tm,n和组相似性yp,iy_{p,i}yp,i都在(0,1)(0,1)(0,1)之间(两者均是针对两张图像之间的关系而言)。该值越高,相似性越大,表示两幅图像属于同一人的可能性越大。
3.2. 通过CRF进行组相似性建模
设OOO表示一个组中的所有图像,首先估计图像组的局部相似性TTT。作者考虑了多尺度局部相似性,而每个尺度中的每个局部相似性都是考虑组内任意两张图像之间的相似性。有:T={Ts}s=1ST=\{T^s\}_{s=1}^ST={Ts}s=1S,而Ts={tm,ns∣Im,In∈O}T^s=\{t_{m,n}^s|I_m,I_n\in O\}Ts={tm,ns∣Im,In∈O},其中TsT^sTs包含尺度s的局部相似性。而
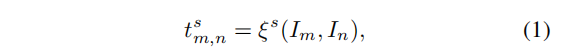
其中ξs(Im,In)\xi^s({I_m,I_n})ξs(Im,In)计算尺度s的特征嵌入ϕs(Im)\phi^s({I_m})ϕs(Im)和ϕs(In)\phi^s({I_n})ϕs(In)的相似性。
组相似建模为随机变量,用于描述probe图像和gallery图像之间的相似性,形成集合Y={yp,i∣Ii∈G}Y=\{y_{p,i}|I_i\in G\}Y={yp,i∣Ii∈G},它们建立在局部相似性的条件上,并且成对(Y,T)(Y,T)(Y,T)建模在连续CRF,描述为Gibbs分布:
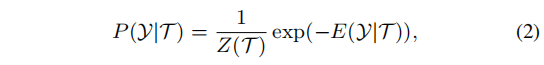
其中Z(T)Z(T)Z(T)是partition函数,E(Y∣T)E(Y|T)E(Y∣T)是能量函数。对于全连接的成对CRF模型,E(Y∣T)E(Y|T)E(Y∣T)可以表示为:
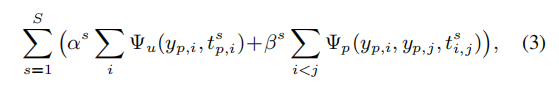
其中,αs\alpha^sαs和βs\beta^sβs是尺度s(仅针对局部相似性)下与一次项(unary)和二次项(pairwise)的有关参数(正的)。其中,一次项为probe图像p和gallery图像i之间的组相似性和局部相似性之间的关系:
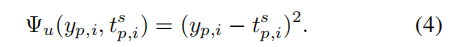
二次项为probe图像p和gallery图像i之间的组相似性,probe图像p和gallery图像j之间的组相似性以及gallery图像i和gallery图像j之间的局部相似性之间的关系:
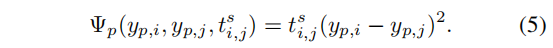
如图2所示:
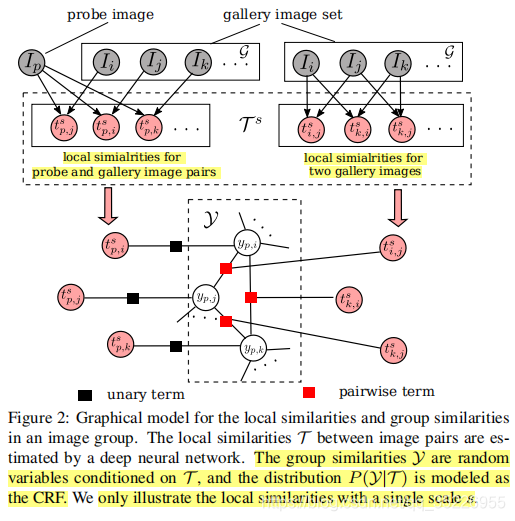
3.3. 近似估计
P(Y∣T)P(Y|T)P(Y∣T)可以由简单的分布Q(Y)Q(Y)Q(Y)来进行估计,而Q(Y)Q(Y)Q(Y)可以由一系列独立的边缘分布的乘积表示,即:
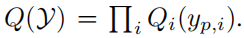
通过最下化P(Y∣T)P(Y|T)P(Y∣T)和Q(Y)Q(Y)Q(Y)两个分布之间的KL散度,让两者的分布尽量一致----即用Q(Y)Q(Y)Q(Y)估计P(Y∣T)P(Y|T)P(Y∣T),从而得到最优分布Qi(yp,i)Q_i(y_{p,i})Qi(yp,i)可以表示为:
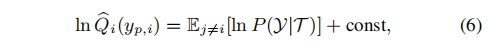

3.4. 用DNN进行CRF建模
CRF模型由multi-scale feature embedding, local similarity estimation和the group similarity estimation三个模块组成。
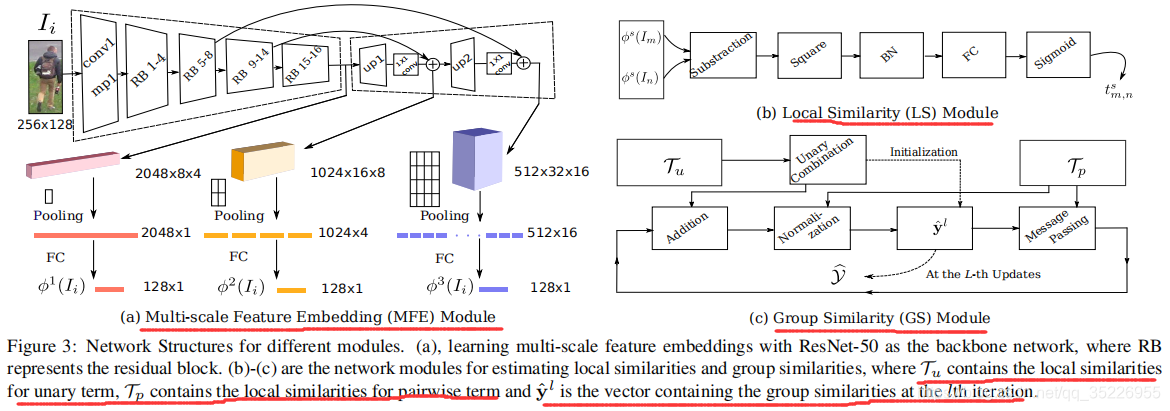
- multi-scale feature embedding模块(MFE):如图3a所示
受Feature Pyramid Network(FPN)启发,该模块用ResNet50作为backbone,通过将自顶向下的路径和横向连接相结合,生成多尺度的高级语义特征图。特别地,自顶向下(top-down)路径采用上采样和1×1卷积来匹配空间维数和特征维数的横向输入。为了获得整个图像的特征图,我们将不重叠的8×4空间池应用于所有尺度的特征图(图3a中用的都是8×4的池化,红橙蓝分别得到2048×1×1,1024×2×2和512×4×4的feature map,然后reshape为2048×1,1024×4和512×16的特征向量)。这种集合策略可以在较大的尺度上部分地保留特征图的空间结构,平衡语义和空间信息。 - Local similarity module模块:如图3b所示
局部相似性tm,nst_{m,n}^stm,ns是基于图像ImI_mIm和图像InI_nIn的尺度s下的特征ϕs(Im)\phi^s({I_m})ϕs(Im)和ϕs(In)\phi^s({I_n})ϕs(In)估计。更具体地,我们计算了两个特征嵌入的差分向量(Substraction),对向量执行一个按元素方向的平方运算(Square),并通过BN层对向量进行规范化。生成的向量通过FC映射到标量,然后进一步通过Sigmoid函数归一化为(0,1),以表示图像ImI_mIm和InI_nIn属于同一人的概率。 - Group similarity module模块:如图3c所示
组相似性Y建立在局部相似性T的条件上,而T可以进一步划分为TuT_uTu和TpT_pTp,其中TuT_uTu是probe图像和gallery图像之间的局部相似性,TpT_pTp是gallery图像pair之间的局部相似性,即:
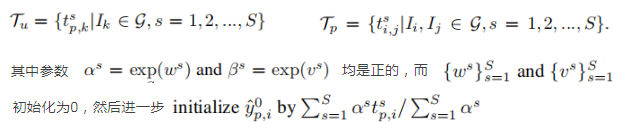
根据式8,组相似性的更新由以下几步组成: - 一次项的线性组合:式8分子第一项,用的是TuT_uTu局部相似性
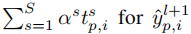
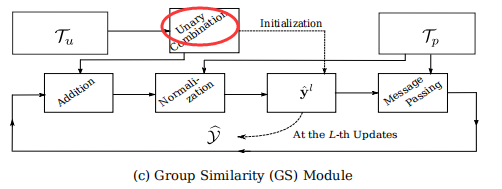
- 消息传递:式8分子第二项
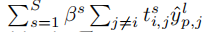
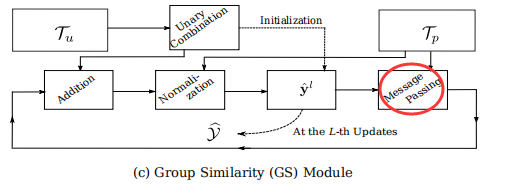

- Norm:除以式8分母的操作,逐元素归一化
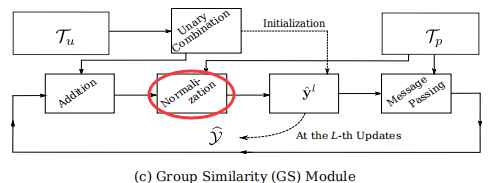

3.5. 整个网络架构
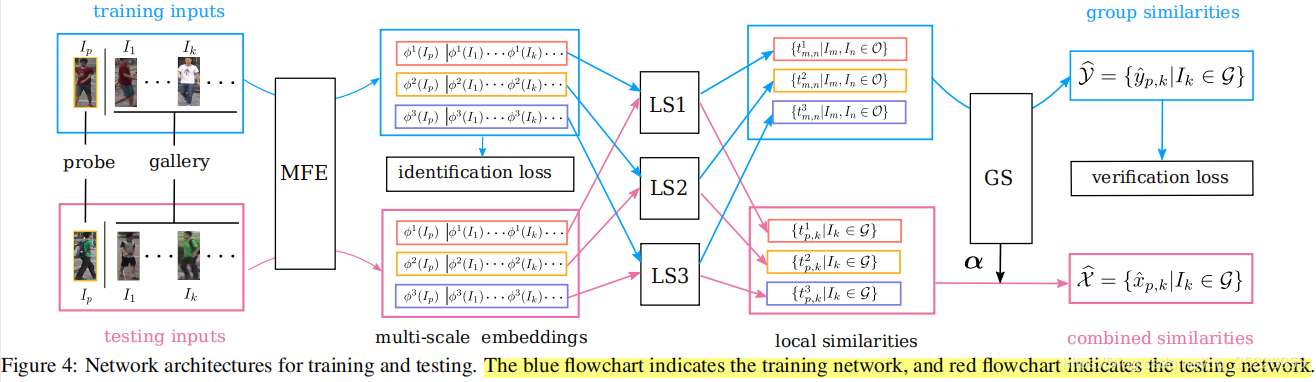
组相似性起着两个作用:(1)考虑到组内不同的依赖关系,指导局部相似性度量的学习;(2)学习线性组合的权重, 为了更准确地估计,需要结合多尺度的局部相似性。在测试中,网络输入可以是任意数量的probe图像和gallery图像,而最终的相似性是多尺度的局部相似性的线性组合,而线性组合的参数
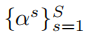
是从GS模块中学习的。最终相似性的美线性组合为:
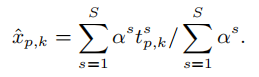
讨论:
训练和测试是采取不一样预测方式的原因是:建立的图是FC的,而测试时gallery非常大,使得训练时学习的消息传递参数
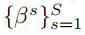
不能直接用于测试。由于局部相似性度量从具有组相似性的学习中受益,式10中的预测相似度可进一步结合多尺度的局部相似性, 不同的测试配置下具有较强的适用性。
3.6. 端到端的优化
- Batch采样:
N_B个人,每个人K_B张图像。取一个人的一张图像为probe,其余为gallery,组成N_B个group。这样,两个gallery图像之间的局部相似性就可以被不同的组重复使用,大大降低了计算量。 - 损失函数:
组相似性表示两张图像属于同一个人的概率,因此使用验证损失,即:
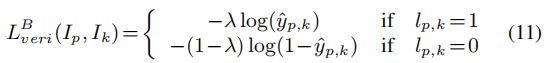
图像I_p和I_k是同一人的图像时,l_p,k=1,否则为0。而lambda是超参,而MFE还需要用OIM损失预测ID:
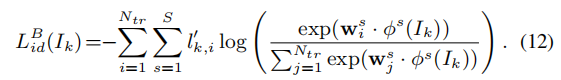
训练集中共N_tr个行人。如果I_k是 i-th 个人的图像,则lk,i′=1l'_{k,i}=1lk,i′=1,否则为0。而wisw^s_{i}wis是 i-th ID的尺度 s 的关联系数。最终损失函数验证损失和ID损失的线性组合。
4. 实验
4.1. 实验细节

4.2. 消融实验

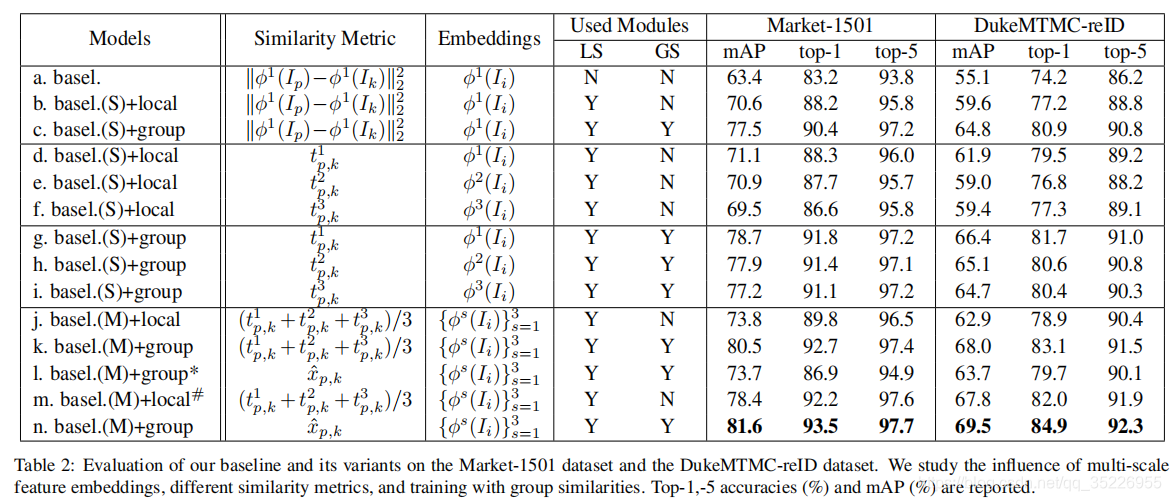
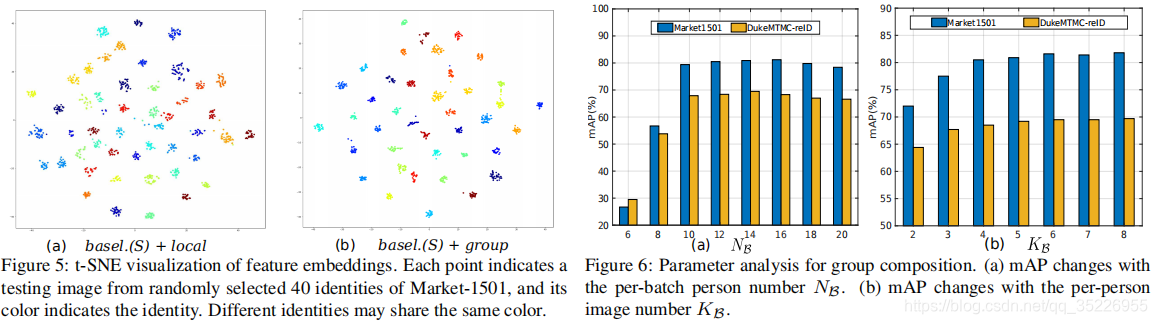
4.3. 和SOTA比较
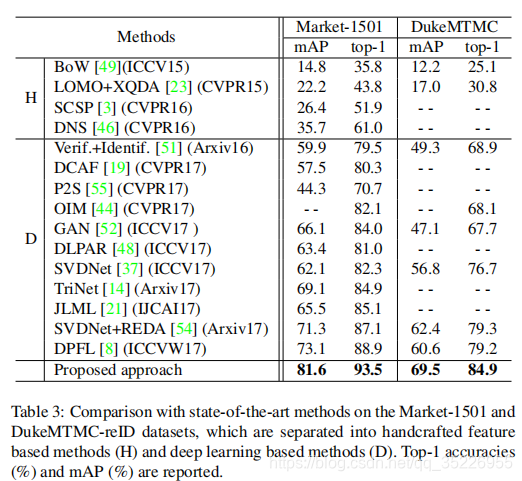
这是2018年的结果,在Market上达到~82%的mAP,性能算是很高的。
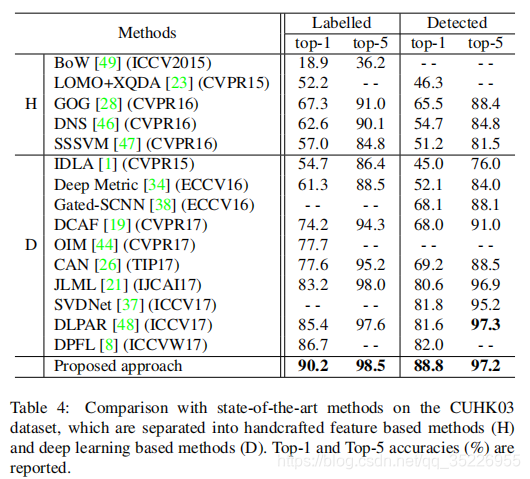







 本文提出一种结合深度条件随机场(DCRF)和深度神经网络(DNN)的组一致性相似性学习方法,用于行人重识别(person re-ID)任务。该方法通过在训练阶段同时考虑局部和组相似性,提高了相似性度量的一致性和准确性。测试时,通过线性组合多尺度的局部相似性进行预测,实现了高性能的人脸识别。
本文提出一种结合深度条件随机场(DCRF)和深度神经网络(DNN)的组一致性相似性学习方法,用于行人重识别(person re-ID)任务。该方法通过在训练阶段同时考虑局部和组相似性,提高了相似性度量的一致性和准确性。测试时,通过线性组合多尺度的局部相似性进行预测,实现了高性能的人脸识别。

















 649
649

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








