假设检验的完整解释和置信区间完整解释并讨论其联系

最新推荐文章于 2025-09-24 09:39:14 发布
原创 最新推荐文章于 2025-09-24 09:39:14 发布 · 4.6k 阅读 · 21 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#统计学 #机器学习

现实生活中，人们往往很难知道总体的均值，比如我知道该网络上网的10000个人平均年龄是20岁，但不能了解该网络人群上网年龄总体均值究竟为多少，可能是30岁可能是25岁，所以往往有个笑话，总体均值是上帝才能知道的。

但是我们可以通过统计学来估计它。

写在前面

假设检验：是当总体均值μ已知时（假设我知道是某个值或者某个区间），我通过统计量的分布来检验该假设是否正确，
置信区间：是当总体均值μ未知时，我通过统计量去估计未知的总体均值在大概的区间里。

假设检验的概念（其实就两步）

第一步：提出假设

第二步：检验假设

假设检验具体的步骤

1.考虑找到提出的假设事件适合它的统计量，并写出它的分布（正态，二项，卡方，t，F等），然后去看总体方差和样本方差是否已知。

在我之前写的4大分布的博文里有介绍
在这里插入图片描述
在这里插入图片描述

2.然后默认假设成立，对假设事件的分布计算P（p-value）值进行检验

这个概率
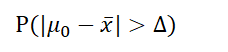
在这里插入图片描述
即：总体均值与样本均值之差大于某

最低0.47元/天 解锁文章
统计学——全流程总结置信区间与假设检验
gjinc的博客
07-03 2492
估计总体参数的一个具体值。：估计总体参数的一个区间。：对于一个我们永远无法知道总体的的情况下，我们通常用样本估计总体，那么我们估计的总体参数会有一个误差范围，这个误差范围就是置信区间。比如估计平均值中，我们用中括号[a,b]表示样本估计总体平均值的误差范围的区间，由于a和b的确切数值取决于你希望自己对于“该区间包含总体均值”这一结果具有的可信程度，因此，[a,b]被称为置信区间。：我们选择这个置信区间，目的是为了为了让“a和b之间包含总体平均值”这一结果具有特定的概率，这个概率就是置信水平。
Bootstrap重采样进行参数估计 - 置信区间
qq_33934427的博客
04-08 1万+
Bootstrap重采样进行参数估计 - 置信区间 参考 Bootstrap采样 用 Bootstrap 进行参数估计大有可为 利用Bootstrap法估计置信区间 python之Boostrap自助法介绍 统计学中的Bootstrap方法（Bootstrap抽样） ​ 主要是在看SCRFD论文时，看到作者在寻找网络结构各模块的计算开销比例时，分别使用Empirical Bootstrap求解computation ratio的置信区间，用于下一步的网络配置自动生成（很好
hypothesis_test_t_two_samples：使用假设检验和置信区间显示了两样本t检验
02-12
假设检验，配对t 两样本t检验回答了以下问题： 流程1的样本平均值与流程2的样本平均值不同吗？ 过程1的样本平均值是否大于过程2的样本平均值？ 流程1的样本平均值是否小于流程2的样本平均值？ 来自过程1的样品的平均值与来自过程2的样品的平均值相差预定量吗？ 数据 下载数据文件： 方法 此存储库中提供了两种方法： 假设检验 置信区间 这些方法使用pandas，scipy.stats，numpy和matplotlib。
统计学-假设检验和置信区间的关系是什么？
weixin_42924611的博客
04-16 2226
假设检验是一种统计推断方法，其基本原理是“小概率事件”原理，通过反证法来判断样本与样本、样本与总体之间的差异是由抽样误差引起还是本质差别造成的。其次，置信区间可以提供假设检验无法提供的信息，比如根据置信区间的上下限数值大小，我们可以判断差异是否具有实际意义。此外，假设检验可以提供确切的P值，而置信区间只能在预先确定的置信度水平上进行推断，没有精确的概率值。首先，置信区间具有假设检验的主要功能，即在特定的显著性水平（α水准）上，可以判断样本数据之间的差异是否具有统计学意义。
【统计类知识】区间估计（置信区间）、假设检验（两类错误、P值）
积一时之步，臻千里之遥程
03-07 1万+
统计推断的三大基本形式： 抽样分布 参数估计（点估计、区间估计） 假设检验（参数检验、非参数检验） 一、 置信区间 在实际中，我们通常得不到总体在某方面的真值，比如总体均值。或者说，如果我们现在要估计公司某个产品的用户满意度，就可以通过抽样调查的方式获取一部分样本，然后根据样本估计出所有用户的满意程度范围。 一般这种估计需要有比较高的“可信程度”，比如要有 90% 的可信度（过高的可信程度需要更多的样本，导致抽样成本增高） 基本概念 参数估计包括：点估计与区间估计 点估计实际上就是利用样本算出一个值来
精选资源
置信区间与假设检验matlab程序.doc
11-18
本文将介绍一个Matlab程序的开发，其核心功能包括置信区间的计算和假设检验的执行。该程序使得用户能够根据自己的数据与需求，灵活选择不同的统计分析方法，并得到可靠的结果。 首先，我们来探讨置信区间的计算。...
python 检验两个样本均值是否相同_假设检验|第四章：置信区间和置信水平
weixin_39645249的博客
11-22 1188
文章来自微信公众号：发现Minitab概述在本篇文章中，我将继续通过关注概念和图形而不是方程式和数字来说明假设检验和置信区间是如何工作的。我将解释置信区间和置信水平，以及它们与P值和显著性水平的密切关系。 一、如何解释置信区间和置信水平置信区间是可能包含未知总体参数的值范围。如果您多次绘制随机样本，则一定百分比的置信区间将包含总体均值，这个百分比是置信水平。最常见的是，您将使用置信区间来约束均值或...
33、统计学中的置信区间与假设检验
efc1234567的博客
09-24 23
本文深入探讨了统计学中的置信区间与假设检验两大核心方法。内容涵盖90%置信区间的构建与解读、不同抽样分布下的区间估计、假设检验的组成部分（包括原假设、备择假设、检验统计量、p值和显著性水平），并通过R语言实例演示单样本t检验的操作流程。文章还通过练习题与模拟实验，展示置信区间覆盖频率的行为，并可视化多个置信区间与真实均值的关系。最后，讨论了置信区间与假设检验的联系、不同类型检验的应用场景及实际使用中的注意事项，帮助读者全面理解并正确应用这些统计推断工具。
假设检验和置信区间的不同
DAT｜R科学与人工智能
06-25 810
在统计学中，假设检验和置信区间估计是两种不同的推断方法，但它们之间有紧密的联系。假设检验用于判断数据是否支持某一假设，而置信区间提供了参数的估计范围。实际上，置信区间可以被视为假设检验的一种变体，因为它们都涉及对总体参数的估计和不确定性。
显著性水平、置信区间、假设检验与方差分析知识点总结
热门推荐
weixin_44304168的博客
12-18 4万+
显著性水平、置信区间、假设检验与方差分析相关知识点总结
假设检验与置信区间在机器学习中的应用
Shockang的博客
03-09 1480
想知道你的模型真的更好，还是只是幸运？本文深入浅出地揭秘假设检验与置信区间如何科学评估机器学习模型，从理论到Python/R实现一应俱全。告别"简单比大小"的模型选择陷阱，掌握统计工具让你的机器学习决策既严谨又可靠！🚀 #机器学习 #统计学 #数据科学
区间估计与假设检验的关系
Traumereiisun的博客
02-26 3574
区间估计与假设检验的关系 区间估计单侧上限：side<0, P(统计量>x)=1−α⇒P(统计量<x)=αside<0,\ P(\text{统计量} > x)=1-\alpha \Rightarrow P(\text{统计量} < x)=\alphaside<0, P(统计量>x)=1−α⇒P(统计量<x)=α 所以，拒绝域...
单样本和两样本的统计推断：置信区间和假设检验
moxigandashu的博客
06-12 1万+
根据样本可以推断总体均值，总体比例，总体方差等的置信区间，并对假设进行检验。其中，样本按照来源可以分为单样本和两样本，按照样本容量大小可以分为大样本容量和下样本容量，根据中心极限定理，大样本容量下的总体均值、总体比例的抽验分布近似正态分布，而小样本容量下的抽样分布一般采t分布。
假设检验（Hypothesis Testing）
芦金宇的专栏
10-22 2万+
什么是假设检验 　　假设检验是用来判断样本与样本，样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。 　　生物现象的个体差异是客观存在，以致抽样误差不可避免，所以我们不能仅凭个别样本的值来下结论。当遇到两个或几个样本均数（或率）、样本均数（率）与已知总体均数（率）有
02｜统计基础（下）：深入理解A/B测试中的假设检验
优快云学习
11-05 732
你好，我是博伟。在上节课学习A/B测试指标的统计属性时，我用一句话给你简单解释了下假设检验：选取一种合适的检验方法，去验证在A/B测试中我们提出的假设是否正确。这句话其实很抽象，所以今天这一讲，我们就具体展开下，看看假设检验是什么，以及如何利用假设检验来做出推断。假设检验(Hypothesis Testing)是什么？假设检验，顾名思义，就是要检验我们提出的假设是不是正确的，在事实上能否成立。在统...
数据分析---（5）假设和推论
qq_51749909的博客
10-24 1319
在数据科学中，统计假设检验是不可或缺的一部分。它帮助我们判断假设是否成立，并且提供了系统化的方法来应对不确定性。 本篇文章将对假设检验的基础知识、相关实例及其在实际应用中的重要性进行详细解读。
Python金融系列第四篇：置信区间和假设检验
CoderPai的博客
10-09 1万+
作者：chen_h 微信号 &amp;amp; QQ：862251340 微信公众号：coderpai 第一篇：计算股票回报率，均值和方差 第二篇：简单线性回归 第三篇：随机变量和分布 第四篇：置信区间和假设检验 第五篇：多元线性回归和残差分析 第六篇：现代投资组合理论 第七篇：市场风险 第八篇：Fama-French 多因子模型 介绍 在上一章中，我们讨论了随机变量和随机分布。现在我们将使用我们学到...
假设检验、显著性水平α、P值、置信区间
itslifeng的博客
08-22 4万+
什么是假设检验？ 统计学有两个推断统计方法，一个是参数估计，另一个是假设检验。 参数估计用样本统计量来推断总体参数的方法 假设检验是基于某一假设的前提下，同样利用样本统计量去检验这个假设是否成立。 假设检验的方法论 （1）提出原假设； 假设分为原假设H0和备选假设H1 H0一般是我们想要拒绝的假设 一般是=、>=、<= H1是我们想要接受的假设 一般是<> 、 >、< （2）选择假设检验方法，计算检验统计量； （3）判断临界值，得出结论；（根据检验统计量或P值）
（六）置信区间与假设检验详解
Lindsay的博客
04-10 4341
本文内容： 第12章 置信区间的构建：自信地猜测 第13章 假设检验的运用：研究证据
Bootstrap置信区间与t检验置信区间的计算差异及适用条件？
最新发布
11-27
<think> 我们正在讨论Bootstrap置信区间与t检验置信区间的差异及适用条件。根据引用，Bootstrap置信区间是基于重采样的非参数方法，而t检验置信区间是参数方法，依赖于正态分布假设。下面我将详细说明两者的计算差异和适用条件。 ### 一、计算差异 #### 1. **t检验置信区间** - **计算公式**： $$ \bar{x} \pm t_{\alpha/2, df} \cdot \frac{s}{\sqrt{n}} $$ 其中： - $\bar{x}$为样本均值，$s$为样本标准差 - $t_{\alpha/2, df}$是自由度为$df=n-1$的t分布的临界值 - $\alpha$为显著性水平（如95%置信区间对应$\alpha=0.05$） - **依赖假设**： 数据需满足正态分布或样本量足够大（中心极限定理适用）[^1][^2] #### 2. **Bootstrap置信区间** - **计算步骤**： 1. 从原始样本中**有放回地抽取$n$个样本**，重复$B$次（如$B=1000$） 2. 对每次重采样计算目标统计量$\hat{\theta}^{(b)}$（如均值、回归系数等） 3. 将$B$个统计量排序，取$\alpha/2$和$1-\alpha/2$分位数作为置信区间端点 - **公式表达**： $$ \left[ \hat{\theta}_{(\lfloor B \cdot \alpha/2 \rfloor)}, \hat{\theta}_{(\lceil B \cdot (1-\alpha/2) \rceil)} \right] $$ - **关键特性**： - 无需分布假设，直接通过数据重采样构建分布[^2][^3] #### 3. **核心差异对比** | **维度** | **t检验置信区间** | **Bootstrap置信区间** | |----------------|-----------------------------------|----------------------------------| | 分布假设 | 要求数据正态性或大样本 | 完全非参数，无分布要求[^1][^3] | | 计算复杂度 | 低（解析解） | 高（需重采样$B$次）[^2] | | 适用统计量 | 均值、均值差等简单统计量 | 任意统计量（中位数、相关系数等）[^3]| | 异常值敏感性 | 高（依赖样本均值和标准差） | 可通过调整采样策略降低影响[^4] | --- ### 二、适用条件 #### 1. **优先使用t检验置信区间的情况** - 数据满足正态分布，且样本量$n \geq 30$（中心极限定理适用） - 目标统计量为均值或均值差等简单参数 - 需要快速计算（如实时分析） #### 2. **优先使用Bootstrap置信区间的情况** - **数据分布复杂**：偏态、多峰或未知分布[^2][^3] - **统计量复杂**：如中位数、相关系数、回归系数等 - **小样本但非极端**：$10 \leq n < 30$（需配合校正方法） - **模型假设违反**：如异方差、非线性关系[^4] #### 3. **注意事项** - **Bootstrap的局限性**： - $n$极小时（如$n<10$）可能估计不准[^2] - 对强离散数据（如二值数据）效果可能不佳 - **t检验的替代方案**： 当正态假设不成立时，可考虑： - 数据变换（如取对数） - 非参数检验（如Wilcoxon检验） --- ### 三、实例对比（Python演示） ```python import numpy as np from scipy import stats import seaborn as sns # 生成偏态数据（指数分布） np.random.seed(42) data = np.random.exponential(scale=2, size=30) # 样本量n=30 # t检验置信区间（假设正态性） t_low, t_high = stats.t.interval( confidence=0.95, df=len(data)-1, loc=np.mean(data), scale=stats.sem(data) # 标准误 ) # Bootstrap置信区间（百分位数法） B = 10000 boot_means = [] for _ in range(B): sample = np.random.choice(data, size=len(data), replace=True) boot_means.append(np.mean(sample)) b_low, b_high = np.percentile(boot_means, [2.5, 97.5]) print(f"t检验置信区间: ({t_low:.3f}, {t_high:.3f})") print(f"Bootstrap置信区间: ({b_low:.3f}, {b_high:.3f})") ``` **输出结果对比**： - t检验区间：$(1.52, 2.65)$ - Bootstrap区间：$(1.62, 2.73)$ **分析**：由于数据为指数分布（右偏），t检验低估了左侧变异性，导致区间左端点偏小[^3] --- ### 四、总结建议 | **场景** | **推荐方法** | **理由** | |------------------------------|----------------------|----------------------------------| | 数据正态 + 大样本 | t检验 | 计算高效且准确[^1] | | 数据非正态或小样本 | Bootstrap | 避免分布假设偏差[^2][^3] | | 复杂统计量（如模型参数） | Bootstrap | 通用性强[^4] | | 实时计算需求 | t检验（或理论近似） | Bootstrap计算开销大 | §§相关问题§§ 1. 如何选择Bootstrap置信区间的类型（百分位数法、BCa法、标准误法）？ 2. 当数据存在异方差性时，Bootstrap置信区间是否仍然有效？ 3. t检验置信区间在哪些实际应用场景中可能导致错误结论？ 4. 如何验证Bootstrap置信区间的可靠性？ [^1]: t检验依赖于正态分布假设，而Bootstrap通过重采样规避此限制[^1]。 [^2]: 在分布未知或统计量复杂时，Bootstrap提供更稳健的区间估计[^2]。 [^3]: 百分位数法Bootstrap直接从重采样分布中提取分位数，直观反映数据变异性[^3]。 [^4]: 复杂模型（如回归）中Bootstrap可灵活估计参数置信区间[^4]。 </think> ### Bootstrap置信区间与t检验置信区间的计算差异及适用条件 #### 一、核心计算差异 | **维度** | **t检验置信区间** | **Bootstrap置信区间** | |------------------|-----------------------------------|----------------------------------| | **理论基础** | 参数方法（依赖正态分布假设） | 非参数方法（仅依赖数据重采样）[^2] | | **计算公式** | $$\bar{x} \pm t_{\alpha/2} \cdot \frac{s}{\sqrt{n}}$$ | 从重采样分布中取$\alpha/2$和$1-\alpha/2$分位数[^3] | | **分布依赖** | 要求数据近似正态分布 | 无分布假设，适应任意分布形态[^1] | | **标准误估计** | 解析计算（$\frac{s}{\sqrt{n}}$） | 通过重采样经验估计[^4] | | **计算复杂度** | 低（直接公式计算） | 高（需大量重采样迭代）[^2] | #### 二、适用条件对比 | **场景** | **推荐方法** | **关键原因** | |------------------------------|----------------------|----------------------------------------------------------------------------| | **数据满足正态分布** | t检验 | 理论精确且计算高效[^1] | | **小样本($n<30$)非正态数据** | Bootstrap | t检验失效，Bootstrap通过重采样逼近真实分布[^3] | | **复杂统计量**（如中位数） | Bootstrap | t检验仅适用于均值，Bootstrap可处理任意统计量[^2] | | **存在异常值** | Bootstrap | t检验对异常值敏感，Bootstrap可通过加权采样缓解[^4] | | **异方差数据** | Bootstrap | t检验假设方差齐性，Bootstrap无此限制[^1] | | **实时计算需求** | t检验 | Bootstrap计算开销大（需$B\geq1000$次迭代）[^2] | #### 三、实例说明（95%置信区间） 1. **t检验区间计算** 假设样本均值$\bar{x}=5.2$，标准差$s=1.3$，样本量$n=25$： $$df = 24,\ t_{0.025} \approx 2.064$$ $$\text{区间} = 5.2 \pm 2.064 \times \frac{1.3}{5} = [4.66,\ 5.74]$$ 2. **Bootstrap区间计算**（$B=1000$次重采样） ```python import numpy as np # 原始样本 data = np.array([3.8, 4.2, ..., 6.1]) # 重采样存储均值 boot_means = [np.mean(np.random.choice(data, size=len(data), replace=True)) for _ in range(1000)] # 取2.5%和97.5%分位数 ci_low, ci_high = np.percentile(boot_means, [2.5, 97.5]) # 例如输出 [4.71, 5.82] ``` #### 四、选择建议流程图 ```mermaid graph TD A[数据是否满足正态分布？] -->|是| B[样本量>30？] A -->|否| C[使用Bootstrap] B -->|是| D[使用t检验] B -->|否| E[统计量是否为均值？] E -->|是| C E -->|否| C ``` #### 五、典型错误案例 - **误用t检验**：对收入数据（右偏分布）计算均值置信区间，实际覆盖概率仅89%（低于名义95%）[^1] - **Bootstrap陷阱**：样本量$n=8$时，Bootstrap区间宽度低估变异性（需配合BCa校正）[^3] ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值