PID经验调参一点理解

最新推荐文章于 2025-06-14 23:42:46 发布
最新推荐文章于 2025-06-14 23:42:46 发布
阅读量1.6k 收藏 14
点赞数
CC 4.0 BY-SA版权
文章标签： matlab pid
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_33795842/article/details/120849365
本文介绍了PID控制器的参数调整方法，首先通过调整比例系数Kp得到2-3个波峰的曲线，然后逐步增加积分系数KI以消除偏差，最后加入微分系数KD使曲线平滑。目标是实现4:1衰减过程，这是一种理想的控制系统过渡状态，能快速接近目标值并保持稳定。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

1、调参原理

      通过传感器采集位置或者速度反馈信号，用串口软件或者matlab做出采集的数据曲线。

      整定步骤：先比例，后积分，再微分。

      将积分系数和微分系数置为0，只保留比例系数Kp

      从1开始慢慢增大比例系数Kp,指导曲线出现两到3个波峰，记录当前的KP，如图1所示

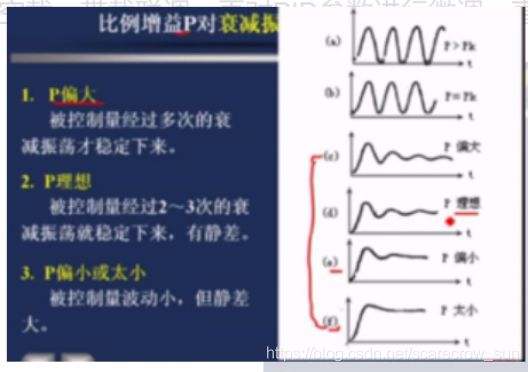
  图1

      加入积分环节KI,逐渐增大KI，直到曲线消除偏差，即曲线稳态值与目标值一致

      此时适当调节KI和KP(调节范围在20%左右)，保证曲线只有2-3个波峰，直到获得4：1衰减过程。如图2所示。

preview

图2 最佳衰减震荡曲线

解释：控制系统在设计、正定和运行中，衡量系统质量的依据就是系统的过渡过程。当系统的输入为阶跃变化时，系统的过渡过程表现为：发散震荡，灯幅震荡，衰减震荡，单调过程等形式，多数情况下，人们都希望看到衰减震荡过程，且认为图2所示的过渡过程最好，并将其作为衡量控制系统质量的依据。其可作为控制系统质量指标的理由是：其第一次恢复到给定值时较快，而后虽然又偏离了，但是偏离不大，且只有极少数几次震荡就能稳定下来。量上分析，第一个波峰B的高度为第二个波峰B的4倍，故而这种曲线又称为4:1衰减曲线，在控制器工程整定时，以能得到4:1的衰减过程为最好，这是的调节器参数可称为最佳参数。

      最后加入KD,使曲线平稳光滑的达到稳态值。

静戴冠
关注
PID参数解析+调参经验笔记（经验法）
2401_85011960的博客
05-17 2820
/增量式PI控制器。return Pwm;return Pwm;
PID参数调整，个人经验（配输出曲线图）
云轩阁
07-30 6万+
系列文章目录 1.元件基础 2.电路设计 3.PCB设计 4.元件焊接 5.板子调试 6.程序设计 7.算法学习 8.编写exe 9.检测标准 10.项目举例 文章目录前言一、控制算法1、PID算法①、PID算法的解析②、PID控制算法讲解③、PID参数解析（一文读懂PID并会调试kp，ki，kd）（位置式+增量式PID）④、STM32——PID恒温控制（含C语言程序）⑤、PID参数调节口诀⑥、PID温度控制参数整定方法⑦、个人经验⑧、Matlab调试 前言 一个普通专科生，拿什么拯救你的未来？
PID算法调参经验分享
m0_73931287的博客
04-02 1万+
​ 本篇文章旨在分享我对PID算法调节参数的经验，觉得掌握PID调参是一种十分重要的技能，在此记录一下。希望我的分享对你有所帮助。有关PID的一些文章，可以参考以下文章。 PID算法参数调节经验分享-优快云博客 PID算法详解（代码详解篇），位置式PID、增量式PID（通用）_pid代码-优快云博客 PID算法详解（精华知识汇总）-优快云博客 ​
一篇图文详解PID调参细节，实现PID入门到精通
最新发布
Java_fenxiang的博客
06-14 1008
在工程中，如果我们要用单片机做一个温控系统，其系统组成一般如下：一个采集温度的ADC，一个输出温度的加热头以及一个用于运行控制算法的单片机，如果我们要维持温度为100度，在不加任何控制算法的情况下，我们可以通过简单的阈值判断法实际曲线(黑线) 在 目标曲线(红线) 周围抖动那如何才能维持实际曲线与目标曲线贴合，达到一个稳定的控制效果呢？这里就引入了PID控制算法的概念，PID是 Proportion Integration Differentiation 的缩写，实际上他就是一个公式，由。
关于PID算法的一些调参经验总结
qq_33001335的博客
06-08 3万+
关于PID算法的一些调参经验总结 前言： 该文为经验学，经验学并不为理论。 不涉及理论，并仅分析过程中遇到的各种问题，以及问题的解决方法。 目录 一、PID算法理解 PID(proportion integration differentiation)其实就是指比例，积分，微分控制，其中Kp为比例系数，Ti为积分时间常量，Td为积分时间常量。 相信来看这篇文章的朋友都不是来看PID算法理解的，但想了想，还是在这里贴出一篇写的十分不错的关于PID算法理解的博客：https://bl
调参经验
aikudexue的博客
03-05 315
参考： https://zhuanlan.zhihu.com/p/24720954?utm_source=zhihu&utm_medium=social
PID调参基础.docx
03-02
为了更好地理解PID调参，我们可以把比例（P）参数看作是响应系统当前状态的关键因素。举个简单的例子，比如我们乘坐的动车在进站时切断动力，火车的进站速度（P值）与距离月台的距离之间的比值，就类似于PID控制中的...
关于无人机PID调参的经验分享
Kyle_Chan_zMH的博客
02-27 5408
关于四旋翼无人机调参经验分享，有过程有总结
Arduino PID库 （3）：调参更改
acktomas的博客
08-04 930
上述现象描述了在系统进入稳态后，突然改变 PID 参数导致的变化，引起输出较大变化的起主要作用的因子为 I 参数，由于进入稳态 P 参数乘以 E 变化不大，D 参数同样不大，但是 I 参数相乘因子是关于时间的积分（可以想象如果一开始被控量与设定值相距较远，而积分表示的是带方向的面积和，所以必然存在一个方向会有较大面积，见下图），所以，会引起较大的变化。换个角度，经典的 PID 控制 I 项，也仅仅是为了消除静态误差而确定的，如果在这个大前提下，换一种方式消除静态误差也是可以的，仅仅是牺牲了。
基于STM32的平衡车细节（调参，扩展）
m0_69390033的博客
12-17 1646
基于STM32的平衡车细节（调参，扩展）
PID参数调节技巧与实践指南
weixin_42511373的博客
05-16 1754
快速响应是衡量控制系统性能的关键因素之一。在工业应用中，一个具有快速响应特性的PID控制器能够使得过程变量迅速地接近设定点，从而减少过渡时间并提高生产效率。在深入探讨了PID控制器的原理、组成、调节方法以及应对非线性和滞后系统的策略之后，本章节将回顾这些主题，并讨论PID技术的发展趋势和未来应用。
深度学习中的调参经验
Begining
08-10 1076
调参其实就是trial-and-error，没有其他捷径可以走。快速尝试, 快速纠错这是调参的关键。 目录 常用的调参经验： 自动调参方法： 这是一个很好的链接, 说明了如何从零开始不断的trial-and-error(其实这里面没遇到什么error): Using convolutional neural nets to detect facial keypoints tutorial...
模型经验调参
weixin_30951231的博客
09-08 192
转载于:https://www.cnblogs.com/xinping-study/p/7494840.html
PID参数整定
weixin_43554366的博客
10-06 1344
一. 采样周期选择 1. 香农采样定理方法 1.1 核心内容 香农采样定理的核心内容为：如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样，那么原始模拟信号就能从采样产生的离散值中完全恢复。 比如一个50Hz的正弦波，采样频率至少要达到 100Hz ，这样才能保证采样后的离散信号能够完整地包含原始信号的所有信息 1.2 PID应用 2. 经验方法 假设电机当前转速为 20RPM，...
PI调节器的一些YY心得
qq_27016651的博客
02-22 1万+
PI调试经验： 最近在调试PI参数时，发现积分环节参数还有挺大的学问：   比如说响应有高频干扰时，最简单通俗的办法就是加一个一阶低通滤波器，一阶低通滤波器的表达式如下： 截止频率 当截止频率越低的时候，滤的越深，但是从波特图可以看出，滤的深也就会造成幅值衰减。 上面是分析的一阶低通滤波器，下面是积分环节，两则竟然有异曲同工之妙   积分的表达式如下： 公式没毛病的，那个...
图文详解PID调参
热门推荐
嵌入式学习记录站点
06-19 11万+
不会PID调参？这篇文章图文结合带你学会PID调参！让你成为PID调参大神！！！
PID参数调节的经验
wsq_666的博客
08-24 9473
PID参数调节经验，已经PI对性能改善作用
那我想实现电机的变频调速应该怎么用pid和pwm
03-14
<think>好的，我需要帮助用户理解如何结合PID算法和PWM技术实现电机的变频调速。首先，用户已经了解了PID和PWM的基本区别和应用场景，现在需要具体指导如何将它们结合起来使用。 首先，我应该明确变频调速的基本概念，可能用户指的是通过改变电机驱动电源的频率来控制转速，这通常用于交流电机如三相异步电机。但用户提到使用PWM，这可能涉及到直流电机或通过PWM模拟交流频率变化的变频控制。需要先确认这一点，但根据常见的应用，可能用户指的是直流电机调速，或者使用PWM来生成可变频率的交流信号。 不过，通常变频调速更多指交流电机的控制，而PWM在直流电机中用于调节电压。可能用户在这里有些混淆，或者想通过PWM调节直流电机的等效电压，进而调速。或者，用户可能想使用PWM生成可变频率的交流信号来控制交流电机。需要明确这一点，但为了覆盖常见情况，假设用户指的是直流电机的调速，使用PWM调节电压，并结合PID来闭环控制转速。 接下来，我需要结构化的步骤来指导用户。首先可能需要系统组成，包括电机、PWM驱动器、反馈装置（如编码器），然后介绍控制流程：设定目标转速，通过传感器获取实际转速，PID计算调整PWM占空比，从而调节电机电压，实现闭环控制。 需要详细说明PID的三个参数如何影响系统，调参的方法，以及PWM频率的选择。同时，可能需要给出伪代码或示例，比如如何将PID输出转换为占空比，处理积分饱和的问题。还要注意硬件方面的考虑，比如电机驱动电路、保护措施等。 可能用户会遇到的问题包括PID振荡、响应速度慢、稳态误差等，需要提供调参建议，比如先用纯比例控制，逐步加入积分和微分。另外，PWM的频率选择也很重要，太高可能导致开关损耗，太低可能引起电机噪音或振动。 还需要考虑反馈信号的获取，比如编码器的分辨率和采样频率，确保反馈的实时性和准确性。如果使用微控制器，需要确保定时器配置正确，中断处理及时。 最后，总结步骤，强调PID和PWM的协同作用，PID作为控制算法提供精确调整，PWM作为执行手段将控制信号转化为实际功率输出。可能还需要提到仿真或实验验证的重要性，先通过仿真调整参数，再实际应用。 检查是否有遗漏点，比如抗积分饱和措施，PWM占空比的范围限制，电机的启动和停止时的特殊处理，以及安全保护机制，如过流保护。确保回答全面且易于理解，避免过于技术化的术语，但保持准确性。</think>在电机变频调速系统中，结合 **PID算法** 和 **PWM技术** 可以实现高精度、动态响应快的闭环控制。以下是具体实现步骤和关键设计要点： --- ### **一、系统组成与原理** | **组件** | **功能** | |------------------|--------------------------------------------------------------------------| | **电机** | 执行机构（直流/无刷直流电机，或通过PWM模拟变频的交流电机） | | **PWM驱动器** | 将控制信号转换为电机驱动电压（如H桥电路、IGBT模块） | | **转速传感器** | 反馈实际转速（编码器、霍尔传感器、测速发电机等） | | **控制器** | 运行PID算法（微控制器如STM32、Arduino，或PLC） | | **目标设定** | 用户输入的目标转速（如通过电位器、通信接口设定） | **控制流程**： 目标转速 $n_{\text{ref}}$ ➔ PID计算误差 ➔ 输出PWM占空比 $D$ ➔ 调节电机电压/频率 ➔ 传感器反馈实际转速 $n_{\text{actual}}$ ➔ 闭环修正。 --- ### **二、详细实现步骤** #### **1. 硬件搭建** - **PWM驱动电路**： - 直流电机：H桥电路（如L298N模块），PWM占空比直接控制电枢电压 $V_{\text{motor}} = D \cdot V_{\text{in}}$ - 交流电机变频：通过PWM生成SPWM（正弦脉宽调制）波形，改变输出频率 $f_{\text{out}}$（需搭配逆变电路） - **反馈传感器**： - 编码器：每转输出固定脉冲数，计算转速 $$n_{\text{actual}} = \frac{\text{脉冲数}}{\text{时间} \times \text{每转脉冲数}} \times 60 \, (\text{RPM})$$ - 霍尔传感器：检测磁场变化，适合无刷电机 #### **2. PID算法实现** - **离散化PID公式**（微控制器中常用）： $$ u(k) = K_p e(k) + K_i \sum_{i=0}^k e(i) \Delta t + K_d \frac{e(k) - e(k-1)}{\Delta t} $$ 其中 $e(k) = n_{\text{ref}} - n_{\text{actual}}(k)$，$\Delta t$ 为采样周期。 - **参数整定方法**： 1. **试凑法**：先设 $K_i=0, K_d=0$，增大 $K_p$ 至系统出现振荡后回调至80%； 2. 加入 $K_i$ 消除稳态误差，但过大会导致超调； 3. 加入 $K_d$ 抑制振荡（注意噪声放大问题）。 #### **3. PWM映射与输出** - **PID输出限幅**：确保输出在PWM有效范围内（如0%~100%占空比）： $$ D = \begin{cases} 0 & \text{if } u_{\text{PID}} \leq 0 \\ \frac{u_{\text{PID}}}{u_{\text{max}}} \times 100\% & \text{if } 0 < u_{\text{PID}} < u_{\text{max}} \\ 100\% & \text{if } u_{\text{PID}} \geq u_{\text{max}} \end{cases} $$ 其中 $u_{\text{max}}$ 对应电机最大允许电压/功率。 - **抗积分饱和（Anti-windup）**：当输出饱和时冻结积分项，避免持续累积误差（见下方代码示例）。 #### **4. 代码示例（伪代码）** ```c // 定义PID参数 float Kp = 0.5, Ki = 0.1, Kd = 0.02; float error, last_error, integral = 0; float max_output = 100.0; // 对应PWM占空比100% void PID_Control(float target_rpm, float actual_rpm) { error = target_rpm - actual_rpm; integral += error * dt; // dt为采样周期 float derivative = (error - last_error) / dt; // 计算PID输出 float output = Kp * error + Ki * integral + Kd * derivative; // 抗饱和处理 if (output > max_output) { output = max_output; integral -= (output - max_output) / Ki; // 反向修正积分 } else if (output < 0) { output = 0; integral -= output / Ki; } // 更新PWM占空比 set_pwm_duty(output / max_output * 100); last_error = error; } ``` --- ### **三、关键设计参数** | **参数** | **典型值/建议** | |-------------------|--------------------------------------------------------------------------------| | **PWM频率** | 直流电机：1-20kHz（高频减少电流纹波）；变频调速：载波频率需远高于输出频率 | | **采样周期** | 10-100ms（需小于系统响应时间） | | **PID调参目标** | 超调量 <5%，调节时间短（如0.5秒内达到稳态） | | **占空比范围** | 根据电机规格设定（如最低启动占空比10%，防止堵转） | --- ### **四、调试与优化** 1. **开环测试**： - 固定PWM占空比，观察电机转速与负载关系，确定 $V_{\text{motor}}-n_{\text{actual}}$ 曲线。 2. **闭环调试**： - 先设 $K_p$ 使系统快速响应，再逐步加入 $K_i$ 消除静差，最后用 $K_d$ 抑制振荡。 - 使用阶跃响应测试（如目标转速从0突变到1000 RPM），记录超调量和稳定时间。 3. **抗干扰测试**： - 人为增加负载（如夹住电机轴），观察系统恢复速度。 --- ### **五、常见问题与解决** | **问题现象** | **可能原因** | **解决方案** | |-----------------------|----------------------------|-------------------------------------------| | **电机转速振荡** | $K_p$ 过大或 $K_d$ 不足 | 降低 $K_p$，增大 $K_d$ | | **稳态误差大** | $K_i$ 过小或采样周期太长 | 增大 $K_i$，缩短采样周期 | | **响应速度慢** | $K_p$ 过小或负载惯性大 | 增大 $K_p$，考虑前馈补偿或模型预测控制 | | **高频噪声干扰** | PWM频率过低或滤波不足 | 提高PWM频率，添加RC滤波电路 | --- ### **六、进阶扩展** - **模糊PID**：针对非线性系统（如大范围变速），通过模糊逻辑动态调整PID参数。 - **磁场定向控制（FOC）**：用于无刷电机的高性能调速，结合PID和PWM实现精准力矩控制。 - **Simulink仿真**：通过模型仿真预调参数（传递函数：$G(s)=\frac{K}{Ts+1}$），减少实物调试时间。 --- **总结**： 1. **PID负责动态决策**：根据目标与反馈的误差，计算所需的控制量； 2. **PWM负责高效执行**：将PID输出转换为电机驱动信号； 3. **协同关键**：合理映射PID输出到PWM占空比，并通过调参平衡响应速度与稳定性。 实际项目中，建议先用仿真工具（如MATLAB）验证算法，再结合硬件逐步调试。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值