2024年数维杯国际赛一文速通B题+全网论文首发+代码分享-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_33690821/article/details/143810962

无附录 30 页论文正文 6 页平替模型 12 页纯可视化无文字

近千种模型组合方案，保证所有资料使用者模型各不相同，千人千面

协同变量辅助的空间插值方法研究与应用——

基于稀疏数据的多维空间估计优化

摘要

随着空间数据应用的不断深入，对空间变量的估计和预测提出了更高的需求，尤其是在采样不足和数据稀疏的情况下。本研究旨在针对空间数据的采样、插值、相关性分析等问题，提出一种基于多种插值方法与协同变量分析的空间数据估计模型。

在数据处理阶段，首先对目标变量和协同变量的数据进行清洗与预处理，包括去除缺失值和异常值，以及构建适用于不同模型的二维空间网格。此外，为了保证模型结果的有效性和一致性，对所有变量进行一致的矩阵变换，以满足后续的模型计算要求。

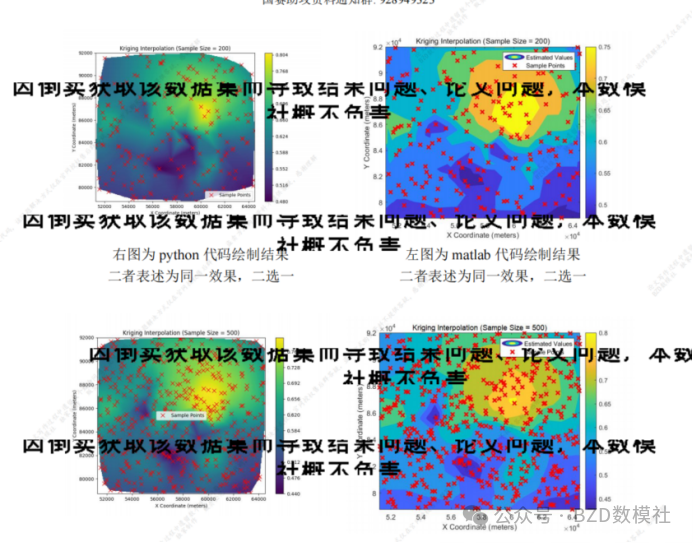
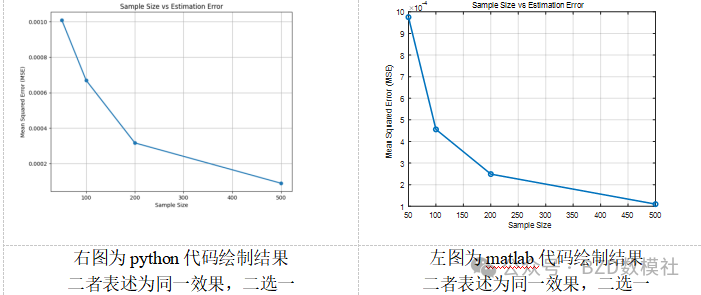
针对问题一，研究了F1目标变量的空间变化模式。随机且均匀地对目标变量进行了重采样，采用拉丁超立方采样方法生成了具有均匀分布的采样点。随后，使用多种插值方法对未采样点进行了估计，并以等值线图展示空间分布结果。通过改变采样数量，进一步分析了样本数量与估计误差（MSE）之间的关系，结果表明采样数量的增加能有效降低估计误差，提升模型精度。

对于问题二，重点研究了目标变量与四个协同变量之间的空间相关性。利用Moran’s I指数衡量空间自相关性，并基于相关性结果选取协同变量1和协同变量2作为最适合的估计协同变量。结果表明，这两个协同变量与目标变量具有显著的空间相关性，可为后续建模提供有效的辅助信息。

在问题三中，进一步利用问题二中确定的协同变量，构建了多种插值模型以研究目标变量的空间变化模式。通过拉丁超立方采样随机选择采样点，同时对目标变量和协同变量进行插值估计。采用了Kriging、线性插值、最近邻插值、三次插值、xxxxxx和xxxxx等六种方法，

关键词：空间插值、协同变量、拉丁超立方采样、Moran’s I、自相关性分析、IDW

一、模型的建立与求解

5.1 数据预处理

5.1.1 数据转化

对于题目给出数据附件中的数据来自于一个矩形区域。矩形区域的结构如下：

（1）X坐标范围：列跨度从51250.0000米到64500.0000米；

（2）Y坐标范围：行跨度从78750.0000米到92000.0000米；

（3）研究区域被划分为50米×50米的小网格，共有266×266个网格点。空间变量的采样值在这些网格点上提供。

整体空间为13,250*13,250米正方形矩阵，分别对应X坐标范围列跨度从51250.0000米到64500.0000米；Y坐标范围：行跨度从78750.0000米到92000.0000米；给出数据为266*266，即组成13,250*13,250米正方形矩阵由266*266个50*50米的正方形小网格组成。如下所示

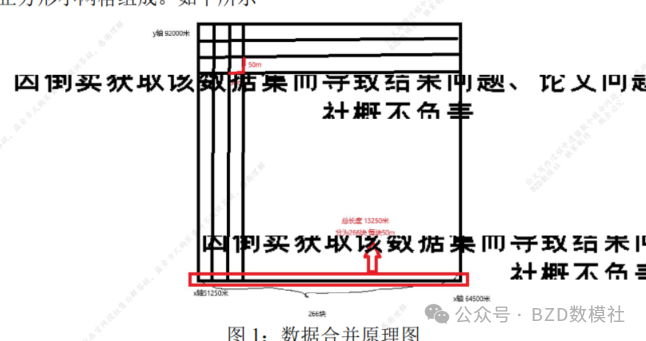
利用这种思路对数据进行汇总整合，得到结果。如下所示

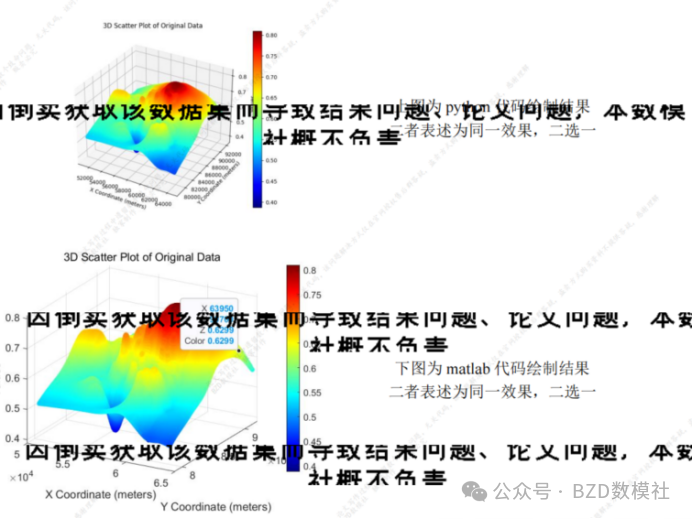
并对原始的数据进行插值，得到在原50米一数据的基础上得到每5米一数据，对比如下所示

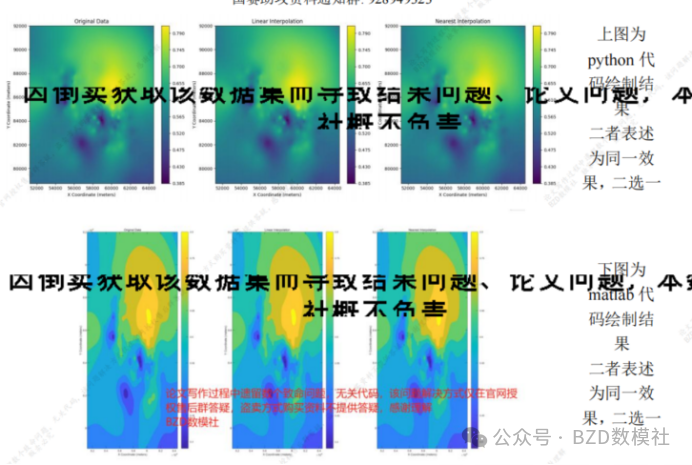
5.1.2 描述性分析

同时，为了进一步对数据进行检验以便处理缺失值、异常值，对题目给出的数据还需要进行必要的描述性分析，例如绘制所有高程数据，进行分析。

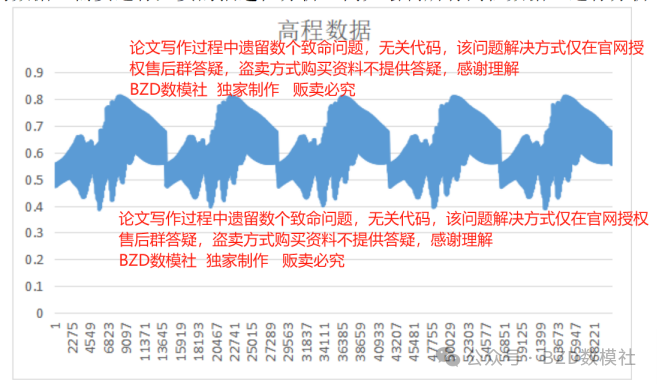
5.2 问题一模型的建立与求解

5.2.1 随机均匀取样

对于问题一随机且均匀地重新抽样目标变量，在空间数据分析中，重采样的目的是从原始数据中选择具有代表性的子集，用于估计未采样位置的空间变量值。由于空间变量通常具有相互依赖性和连续性，因此选择合理的重采样方法对于获取准确的空间分布和趋势至关重要。若采样点过于集中于特定区域，则无法充分代表整个区域的变化特征；而若采样过于随机，则可能会导致样本代表性不足。在本题目中，采用了拉丁超立方采样（Latin Hypercube Sampling, LHS）方法，旨在确保每个采样点在研究区域内均匀分布，进而提高插值的准确性。