二叉树的查找

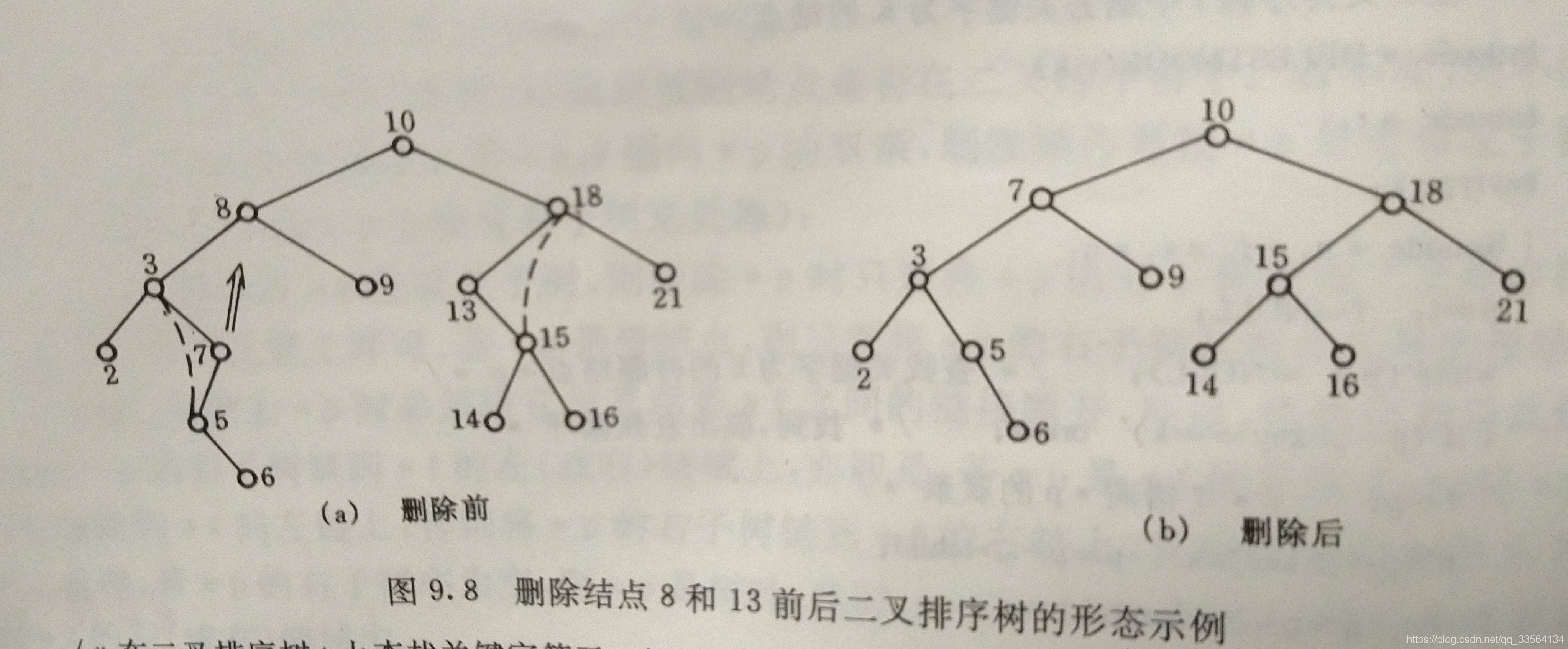
#include<iostream>
#include<stdlib.h>
using namespace  std;
#define M 100
typedef struct node /*二叉链表结点结构*/
{
    int data;  /*数据域*/
    struct node *lchild, *rchild;/*左、右孩子域*/
} bitree;

/*
 * 二叉树的插入算法，保证了中序遍历按顺序排列，思想为：
 * 1.由找到双亲节点f所在位置
 * 2.进行插入
 * 因为一旦中序遍历输出是有顺序的，那么第二大的节点是双亲节点，小的为左子，大的为右子,这样的算法
 * 无非是利用了树的特点
*/
bitree* insertTree(bitree *t,bitree *s)//t为建立好的树，s为插入的数的节点
{
    bitree *f,*p;//f记录了双亲的位置，p则是为了保留t地址不变
    p=t;
    while(p!=NULL)//找双亲
    {
        f=p;//f指向双亲
        if(s->data==p->data) return t;//树中已有节点，无序进行插入
        if(s->data<p->data)p=p->lchild;
        else
            p=p->rchild;
    }
    if(t==NULL) return s;//原树为空，s将作为根节点
    if(s->data<f->data)f->lchild=s;
    else f->rchild=s;
    return t;
}
/*
 * 由于存在了插入算法，所以树的创建可以是一直调用插入算法去生成
*/
bitree* useInsertCreate()
{

   bitree *t,*s;//t为树，s为插入的节点
   t=NULL;
   int data;//节点的信息
   cin>>data;
   while(data!=0)
   {
       s=new bitree;
       s->data=data;
       s->lchild=s->rchild=NULL;
       //待插入的节点准备完毕，现在进行插入
       t=insertTree(t,s);
       cin>>data;
   }
   return t;
}
/*
 * 中序遍历输出
*/
void inorder(bitree *t)  /*中序遍历二叉树的递归算法*/
{
    if (t != NULL)
    {
        inorder(t->lchild);
        printf("%d ", t->data);
        inorder(t->rchild);
    }
}
/*
 * 删除算法（p为删除点，f为p的双亲）：考虑两种情况
 * 1.假设p无左子节点，则p为f的左子（右子），将p的右子放到f的左子（右子）上,p为根时，直接p右子作为根
 * 2.法一：假设p存在左子，可能存在右子，将p的左子放在f的左子上，p的右子放到p的左子的最偏右最下方右子的右子上
 *   法二：找到p的左子的最偏右最下方右子s，让p的节点值取代删除节点的值之后delete p,具体操作如下：
 * 寻到s的双亲节点，由于s是最右边最下面的节点，故s的双亲节点q存在右节点s，s因为不存在左节点，故可以让q的右节点是s的左节点。
 *
*/
bitree* deleteTree(bitree* t,int k)//t为树，k为要删除的节点的值
{
    bitree *p,*f;//p为了保留t的地址不变，同时记录了删除节点的信息，f为双亲
    p=t;
    f=NULL;

    while(p!=NULL)//找到要删除的节点的双亲的位置f，p在这次循环中记录了删除节点的信息
    {
        if(p->data==k)break;
        f=p;
        if(p->data>k)p=p->lchild;
        else p=p->rchild;
    }
    if(p==NULL) return t;//找不到删除的节点
    //情况1，p无左子
    if(p->lchild==NULL)
    {
        if(f==NULL)t=p->rchild;//p为根的情况
        else if(f->lchild==p)
        {
            f->lchild=p->rchild;
        }
        else
        {
            f->rchild=p->rchild;
        }
        delete p;
    }
    //情况2,p有左子，可能存在右子
    else
    {
        bitree *q=p;//q为s的双亲节点，s为最右边最下面的节点
        bitree *s=p->lchild;//s为p的左子
        while(s->rchild!=NULL)//寻找p左子的最偏右最下方的右子
        {
            q=s;s=s->rchild;
        }
        if(p==q)q->lchild=s->lchild;//s无右子
        else  q->rchild=s->lchild;//p存在右子
        p->data=s->data;
        delete s;
    }
    return t;
}
int main()   /*主函数*/
{
    bitree *root;
    root = useInsertCreate();
    root=deleteTree(root,3);
    inorder(root);
    return 0;
}
/*
 * 1 3 5 6 7 0
 * 1 5 6 7 按 <RETURN> 来关闭窗口...
*/