数据结构之最短路径

  数据结构是程序设计的重要基础，它所讨论的内容和技术对从事软件项目的开发有重要作用。学习数据结构要达到的目标是学会从问题出发，分析和研究计算机加工的数据的特性，以便为应用所涉及的数据选择适当的逻辑结构、存储结构及其相应的操作方法，为提高利用计算机解决问题的效率服务。
  数据结构是指数据元素的集合及元素间的相互关系和构造方法。元素之间的相互关系是数据的 逻辑结构，数据元素及元素之间关系的存储称为 存储结构(或物理结构)。数据结构按照逻辑关系的不同分为 线性结构和 非线性结构两大类，其中，非线性结构又可分为树结构和图结构。
  图是比树结构更复杂的一种数据结构。在线性结构中，除首结点没有前驱、末尾结点没有后继外，一个结点只有唯一的一个直接前驱和唯一的一个直接后继。在树结构中，除根结点没有前驱结点外，其余的每个结点只有唯一的一个前驱(双亲) 结点和多个后继 (子树) 结点。而在图中，任意两个结点之间都可能有直接的关系，所以图中一个结点的前驱结点和后继结点的数目是没有限制的。

1、单源点最短路径

  所谓单源点最短路径，是指给定带权有向图 G 和源点 v₀，求从 v₀ 到 G 中其余各顶点的最短路径。迪杰斯特拉 (Dijkstra) 提出了按路径长度递增的次序产生最短路径的算法，其思想是：把网中所有的顶点分成两个集合 S 和 T，S 集合的初态只包含顶点 v₀，T集合的初态为网中除 v₀ 之外的所有顶点。凡以 v₀ 为源点，已经确定了最短路径的终点并入 S集合中，顶点集合 T则是尚未确定最短路径的顶点的集合。按各顶点与 v₀ 间最短路径长度递增的次序，逐个把 T集合中的顶点加入到S集合中去，使得 v₀ 从到 S集合中各顶点的路径长度始终不大于从 v₀ 到T集合中各顶点的路径长度。
  对于下图 所示的有向网，用迪杰斯特拉算法求解顶点 v₀ 到达其余顶点的最短路径的过程如表 3-1 所示。

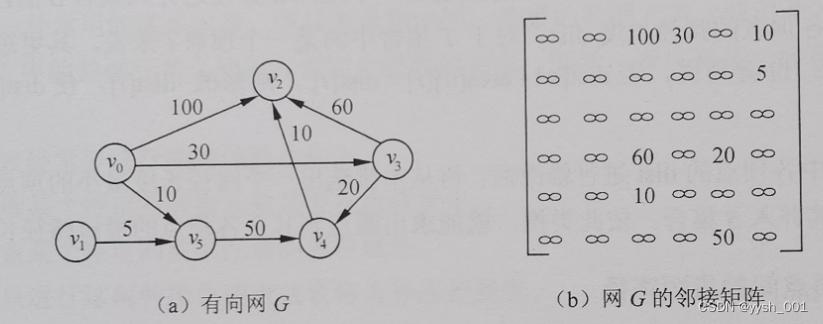
终点	1	2	3	4	5
v1	∞	∞	∞	∞	∞
v2	$$\begin{gathered} 100 \\ (v_0,v_2) \end{gathered}$$	$$\begin{gathered} 100 \\ (v_0,v_2 \end{gathered}$$