本文详细介绍了ConcurrentHashMap的插入过程，包括通过spread()方法减少哈希碰撞，initTable()初始化表，以及tabAt()获取节点在数组中的位置。在节点迁移过程中，文章详细阐述了普通节点和链表节点的迁移策略，特别是在扩容时如何根据高位和低位节点重新分布到新表中。
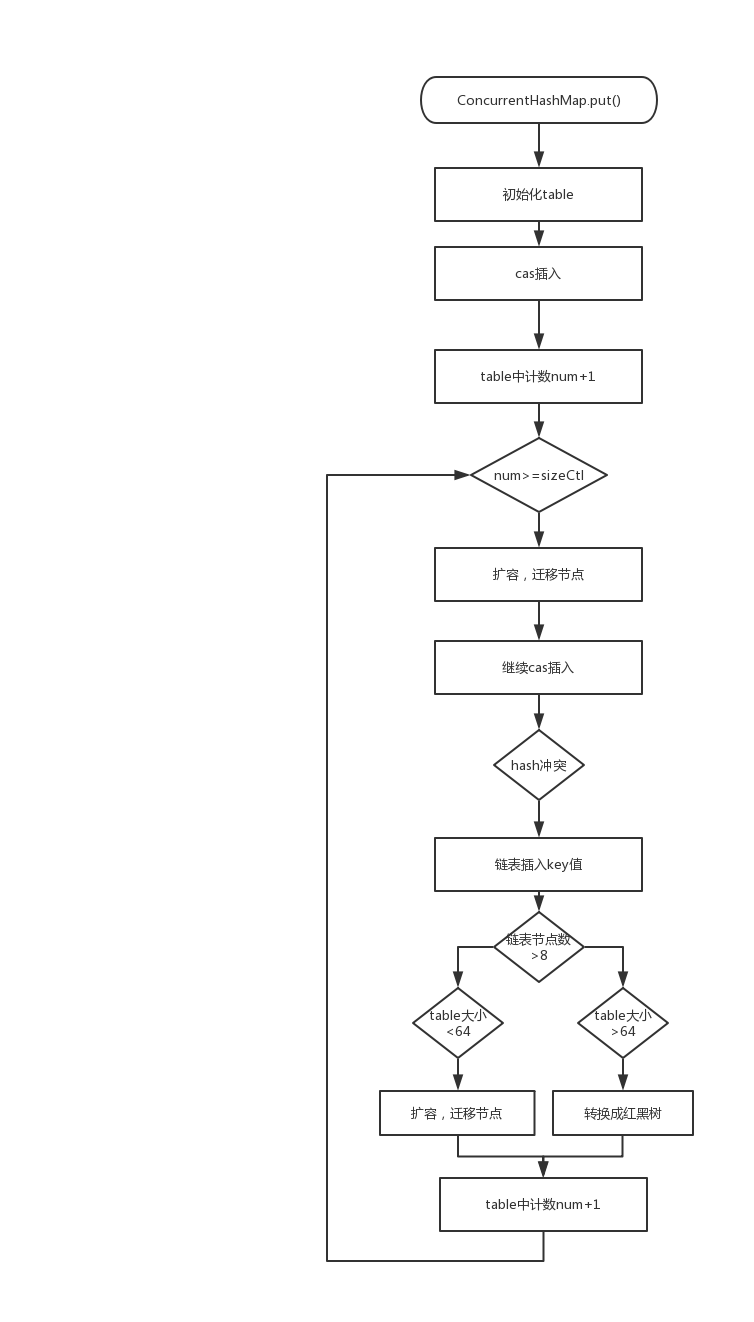
Map元素插入过程图：
/**
*
* onlyIfAbsent 默认为false,即在key值相同的时候，用新的value值替换原始值
*/
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
//获取key对应的hash值 ①
int hash = spread(key.hashCode());
//链表的长度，开始值为0；当hash值冲突时，key值不同，则会插入到链表中
int binCount = 0;
//在数组中插入node节点
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
//如果map中什么都没有，则为最开始put元素，此时去初始化table
if (tab == null || (n = tab.length) == 0)
//② 初始化table,之后再执行下一步插入node
tab = initTable();
//初始化table后，下一次循环到这里，第一次插入元素时，这个位置肯定是空的
//这里就是查找key对应数组位置是否有node,没有则创建node节点，放入数组中
//③ 获取对应位置的node
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
//对应位置为空，则创建节点并插入
if (casTabAt(tab, i, null,
new Node<K,V>(hash, key, value, null)))
break; // no lock when adding to empty bin
}
//扩容时，会在数组最后添加forward节点，
//此时节点的hash值为-1，表示有线程在执行扩容操作
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
//对应的节点不为空，也不是扩容标识节点，则说明发生hash冲突
//若是链表，则通过链表方式添加
//若是红黑树，则通过红黑树方式添加
V oldVal = null;
//同步操作
synchronized (f) {
if (tabAt(tab, i) == f) {
//fh = f.hash
if (fh >= 0) {
//设置链表长度为1
binCount = 1;
//遍历位置的链表，若只有1个节点，则在节点后直接添加
//若链表中有相同的key值，则替换其value,这里应该与hashMap中一致的
for (Node<K,V> e = f;; ++binCount) {
K ek;
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
//默认替换，如果onlyIfAbsent为ture,则不替换旧值
if (!onlyIfAbsent)
e.val = value;
break;
}
Node<K,V> pred = e;
if ((e = e.next) == null) {
pred.next = new Node<K,V>(hash, key,
value, null);
break;
}
}
}
//如果对应的节点时一个红黑树结构，则使用红黑树的方式插入
else if (f instanceof TreeBin) {
Node<K,V> p;
binCount = 2;
if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent)
p.val = value;
}
}
}
}
//链表的长度不为0且大于8的时候，
//并且table的size>64时，将链表结构转化成红黑树；
//否则，将table的size()*2 即调用 tryPresize（）
if (binCount != 0) {
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i);
if (oldVal != null)
return oldVal;
break;
}
}
}
//当前table中有多少元素+1，为了判断是否需要扩容用
addCount(1L, binCount);
return null;
}① spread(key.hashCode())
static final int spread(int h) {
return (h ^ (h >>> 16)) & HASH_BITS;
}将native实现的hash值重新组装，目的是为了减少hash碰撞。
实现：将hash值得低16位和高16位做异或运算，然后& 0x7fffffff,目的是将最高位置为0,保证了hash值的大小在int范围内。
② initTable（）
private final Node<K,V>[] initTable() {
Node<K,V>[] tab; int sc;
//这里涉及多线程的自旋处理，使用while循环，保证初始化成功
//sizeCtl表示map中的key数量超过该数的时候，需要扩容。sizeCtl=map.size()*0.75
//初始化的值为0
//当sizeCtl<0,表示已经有线程在做初始化操作或者在做扩容操作，所以这时候，需要该
//线程让出时间片，让正在执行初始化线程工作。该线程自旋
while ((tab = table) == null || tab.length == 0) {
if ((sc = sizeCtl) < 0)
Thread.yield(); // lost initialization race; just spin
//cas原理，控制线程并发，
//一个线程进入初始化后，SIZECTL 的值被设置为-1，其他线程不能进行初始化操作了
//table初始化时，sc=sizeCtl=0
else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
try {
if ((tab = table) == null || tab.length == 0) {
int n = (sc > 0) ? sc : DEFAULT_CAPACITY;
//初始化一个node数组，大小为 DEFAULT_CAPACITY
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
table = tab = nt;
//很厉害 用公式（n - (n >>> 2)）来计算0.75
sc = n - (n >>> 2);
//此时table已经初始化，sc = 16- 16/(2的2次方)=12
}
} finally {
//sizeCtl=12= table的size*0.75(16*0.75)
//这个值就是下次table中的key超过扩容的值（超过该值，就需要开始扩容了）
sizeCtl = sc;
}
break;
}
}
return tab;
}③tabAt(tab, i = (n - 1) & hash)
(n-1) & hash 在n为2的幂次方时 = hash%n ,这里也解释了为什么n为2的幂次方比较好。这样的计算速度快。
tabAt（）也就是获取 key值在数组tab中的位置的node对象
/**
* 这个方法在putAll()和treeifyBin()的时候调用
* 目的是扩容
*
*
*/
private final void tryPresize(int size) {
int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY :
tableSizeFor(size + (size >>> 1) + 1);
int sc;
while ((sc = sizeCtl) >= 0) {
Node<K,V>[] tab = table; int n;
//这里应该是putAll()的时候会调用。这时候初始化table
if (tab == null || (n = tab.length) == 0) {
n = (sc > c) ? sc : c;
if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
try {
if (table == tab) {
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
table = nt;
sc = n - (n >>> 2);
}
} finally {
sizeCtl = sc;
}
}
}
else if (c <= sc || n >= MAXIMUM_CAPACITY)
break;
else if (tab == table) {
int rs = resizeStamp(n);
//sc只有在一个线程正在迁移的时候，才会为负数，这里是为了解决线程并发问题
//并发线程 这里可以协助迁移
//下一次while循环时。该值sc=sizeCtl
if (sc < 0) {
Node<K,V>[] nt;
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
transferIndex <= 0)
break;
//并发线程协助迁移 ，这里nt = nextTable,是新建的扩容后的table
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
transfer(tab, nt);
}
else if (U.compareAndSwapInt(this, SIZECTL, sc,
(rs << RESIZE_STAMP_SHIFT) + 2))
transfer(tab, null);
}
}
}private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
int n = tab.length, stride;
if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE)
stride = MIN_TRANSFER_STRIDE; // subdivide range
if (nextTab == null) { // initiating
try {
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1];
nextTab = nt;
} catch (Throwable ex) { // try to cope with OOME
sizeCtl = Integer.MAX_VALUE;
return;
}
nextTable = nextTab;
transferIndex = n;
}
int nextn = nextTab.length;
ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab);
boolean advance = true;
boolean finishing = false; // to ensure sweep before committing nextTab
for (int i = 0, bound = 0;;) {
Node<K,V> f; int fh;
while (advance) {
int nextIndex, nextBound;
if (--i >= bound || finishing)
advance = false;
else if ((nextIndex = transferIndex) <= 0) {
i = -1;
advance = false;
}
else if (U.compareAndSwapInt
(this, TRANSFERINDEX, nextIndex,
nextBound = (nextIndex > stride ?
nextIndex - stride : 0))) {
bound = nextBound;
i = nextIndex - 1;
advance = false;
}
}
if (i < 0 || i >= n || i + n >= nextn) {
int sc;
if (finishing) {
nextTable = null;
table = nextTab;
sizeCtl = (n << 1) - (n >>> 1);
return;
}
if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) {
if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT)
return;
finishing = advance = true;
i = n; // recheck before commit
}
}
else if ((f = tabAt(tab, i)) == null)
advance = casTabAt(tab, i, null, fwd);
else if ((fh = f.hash) == MOVED)
advance = true; // already processed
else {
synchronized (f) {
//普通节点迁移 ⑧
if (tabAt(tab, i) == f) {
Node<K,V> ln, hn;
if (fh >= 0) {
//fh = f.hash
//runBit 标识值，
//如果原fh & n 的结果为0，扩容后 fh&2n 的结果也是0
//如果原fh & n 的结果为1，扩容后 fh&2n 的结果也是1
//这个值就是用来判断 扩容后，链表中的节点是否迁移到i+n位置处
int runBit = fh & n;
Node<K,V> lastRun = f;
//获取lastRun,就是最后一个需要迁移的node
for (Node<K,V> p = f.next; p != null; p = p.next) {
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
if (runBit == 0) {
ln = lastRun;
hn = null;
}
else {
hn = lastRun;
ln = null;
}
//遍历链表，这里实现了将链表顺序倒排
//获取到节点后，将之前的节点作为next节点插入。
//lastRun还是最后一个next
for (Node<K,V> p = f; p != lastRun; p = p.next) {
int ph = p.hash; K pk = p.key; V pv = p.val;
if ((ph & n) == 0)
ln = new Node<K,V>(ph, pk, pv, ln);
else
hn = new Node<K,V>(ph, pk, pv, hn);
}
//这里将node节点插入到了table中
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
else if (f instanceof TreeBin) {
TreeBin<K,V> t = (TreeBin<K,V>)f;
TreeNode<K,V> lo = null, loTail = null;
TreeNode<K,V> hi = null, hiTail = null;
int lc = 0, hc = 0;
for (Node<K,V> e = t.first; e != null; e = e.next) {
int h = e.hash;
TreeNode<K,V> p = new TreeNode<K,V>
(h, e.key, e.val, null, null);
if ((h & n) == 0) {
if ((p.prev = loTail) == null)
lo = p;
else
loTail.next = p;
loTail = p;
++lc;
}
else {
if ((p.prev = hiTail) == null)
hi = p;
else
hiTail.next = p;
hiTail = p;
++hc;
}
}
ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) :
(hc != 0) ? new TreeBin<K,V>(lo) : t;
hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) :
(lc != 0) ? new TreeBin<K,V>(hi) : t;
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
}
}
}
}
}⑧普通节点迁移
链表节点迁移：
一、这里先遍历链表，找出其中因为扩容后，节点hash值会变化的（即为原位置+扩容值）的node,作为lastRunNode,
方便后续创建新的链表时，做一个界限判断。
二、循环遍历链表，直到遇到lastRunNode,将链表中的节点重新分配，分为高位节点后低位节点，分别放入table中。这里高位、低位就是扩容前后table的范围变大之后，前面空间和后面空间的意思。
参考：
https://segmentfault.com/a/1190000016124883
http://www.zijin.net/news/tech/339960.html
扫一扫
1626
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
