OPENGL 投影矩阵原理

前言

原文地址http://www.songho.ca/opengl/gl_projectionmatrix.html，英语好的小伙伴可以去阅读原文，可能理解的更好一些，这里只是按我的理解来翻译的，以方便自己日后查看，文中所用到的图片均来自原文。

总览

我们都知道设备屏幕都是2D的，3D的内容最终都会投射到2D的屏幕上去，GL_PROJECTION矩阵就是做这种变换的，他首先将观察坐标转换到裁切坐标，再通过每个坐标除以裁切坐标中的w参数（齐次坐标）映射到设备标准坐标（NDC），所以GL_PROJECTION集成了以上两种变换。
要注意在除以$w_c$(下表c表示在clip裁切坐标中）之前，平截锥体已经完成了裁切的功能。裁切坐标中的$x_c$,$y_c$,$z_c$都是通过和$w_c$做对比来做裁切的。如果裁切坐标小于-$w_c$或者大于$w_c$，那么顶点就会被丢弃。
-$w_c$< $x_c$,$y_c$,$z_c$ < $w_c$
opengl会重构那些边缘被裁切掉的多边形结构

透视投影

在透视投影中，平截锥体中3D的点会被映射到NDC的立方体坐标中；其中x的坐标范围[l,r]在[-1.1]之间；y的坐标范围[b,t]在[-1,1]之间；z的坐标范围[-n,-f]在[-1,1]范围之间。
要注意观察坐标采用的是右手坐标系而NDC(normalized device coordinates，标准设备坐标系）中使用的是左手坐标系（从上图蓝色z坐标指向能看出来是相反的），所以在观察坐标中，在原点的摄像机总是看向-Z的方向，而在NDC中是看向Z的方向。glFrustum只能接受near和far之间距离的正值参数，所以我们需要在构造GL_PROJECTION矩阵的时候对他们取反。

在OpenGL中，观察空间中的3D的点是投影到近平面上（near）的。下面的图展示观察坐标中($x_e$,$y_e$,$z_e$)坐标是如何投影到近平面(near)上对应得($x_p$,$y_p$,$z_p$)坐标的。
（顶视图）

(侧面图）

从平截锥体顶视图上，我们可以看到通过相似三角形原理观察坐标的$x_e$被映射到了$x_p$坐标上：
$\frac{x_p}{x_e}=\frac{-n}{z_e}$
$x_p=\frac{x_e\cdot n}{-z_e}$
从侧面图上，我们也可以看到同样的方法$y_e$投射到了$y_p$坐标上
$\frac{y_p}{y_e}=\frac{-n}{z_e}$
$y_p=\frac{y_e\cdot n}{-z_e}$
我们会发现$x_p$和$y_p$都会依赖于$z_e$他们和$-z_e$成反比。观察坐标通过GL_PROJECTION矩阵变换后，裁切坐标依然是一个齐次坐标。最终他通过除以裁切坐标的w分量转换到NDC空间。
$$\left[\begin{array}{c}{x}_{clip}\\ y_{clip}\\ z_{clip}\\ w_{clip}\end{array}\right]=M_{projection}\cdot \left[\begin{array}{c}{x}_{eye}\\ y_{eye}\\ z_{eye}\\ w_{eye}\end{array}\right]$$

$$\left[\begin{array}{c}{x}_{ndc}\\ y_{ndc}\\ z_{ndc}\end{array}\right]=\left[\begin{array}{c}{x}_{clip}/w_{clip}\\ y_{clip}/w_{clip}\\ z_{clip}/w_{clip}\end{array}\right]$$
因此，我们把裁切坐标系的w分量当做-$z_e$。把GL_PROJECTION矩阵第四行设置为(0,0,-1,0)

接下来，我们通过线性关系将$x_p$和$y_p$映射到NDC里面的$x_n$和$y_n$；
[l,r]->[-1,1],[b,t]->[-1,1]。




然后，我们把$x_p$和$y_{p}1$带入以上等式


注意，我们让等式的每一项都除以-$z_e$来实现透视结果（$x_c/w_c$,$y_c/w_c$）。而我们之前就设定过$w_c$和-$z_c$一致，括号中的项就是裁切坐标的$x_c$和$y_c$。
从以上等式，我们得出了GL_PROJECTION矩阵的第一行和第二行内容。

现在我们只有GL_PROJECTION矩阵的第三行还未完成。我们发现$z_n$和别的项有点区别因为$z_e$在观察空间是投影到-n的近平面上的。但是我们需要唯一的z值来做裁切和深度测试。因而，我们应该对该值取消投影变换。因为我们知道z不依赖于x和y值，我们借助w分量来寻找$z_n$和$z_e$之间的关系。因此，我们可以假设第三行的内容如下：

在观察空间，$w_e$值为1.因此，等式就变成了
$z_n=\frac{A{z}_e+B}{-z_e}$
为了得出系数值，A和B，我们使用($z_e,z_n$)关系；(-n,1)和(-f,1)，将他们带入以上等式。

为了解出等式，我们重写下(1)为B的等式；
B=An-n (1*)
我们将（1*）B的等式带入（2）方程，得到A的等式

将A代入（1）得出B

我们得出了A和B。因此，$z_e$和$z_n$的关系就是：
$z_n=\frac{-\frac{f+n}{f-n}{z}_e-\frac{2fn}{f-n}}{-z_e}$ (3)
最终我们得出了整个GL_PROJECTION的矩阵。完整的投影矩阵如下：

(OpenGL Perspective Projection Matrix)

该投影矩阵属于常规平截锥体。如果观察参数都是对称的，r=-l,t=-b，那么就有简单的方程组：
$\{\begin{array}{l}r+l=0\\ r-l=2r(width)\end{array},\{\begin{array}{l}t+b=0\\ t-b=2t(height)\end{array}$
$$\left[\begin{array}{cccc}\frac{n}{r}& 0& 0& 0\\ 0& \frac{n}{t}& 0& 0\\ 0& 0& \frac{-(f+n)}{f-n}& \frac{-2fn}{f-n}\\ 0& 0& -1& 0\end{array}\right]$$
在我们继续学习之前，我们再看下等式（3），看下$z_e$和$z_n$之间的联系。你注意到这是一个有理函数并且$z_e$和$z_n$之间是非线性关系。也就是说在近平面他有很高的精度而在远平面则有较低的精度。如果[-n,-f]之间距离很大，就会造成深度精准问题（z-fighting）;在远平面附近$z_e$点微小的变化是不会影响到$z_n$的值得。n和f之间的距离应该尽可能的小来减少深度缓存的精度问题。

正射投影

构建正射投影的GL_PROJECTION要比透视投影的矩阵简单的多。
所有观察空间的$x_e$，$y_e$和$z_e$分量都可以线性的映射到NDC上。我们只需要缩放一个固定值到这个正方体上，然后移动到坐标原地。让我们用线性关系来找出GL_PROJECTION的各个元素。






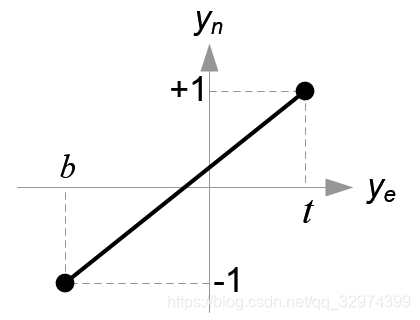
因为w分量对正射投影来说不是必须的，所以GL_PROEJCTION第四行就保持为(0,0,0,1)。因此，完整的正射投影GL_PROJECTION的矩阵为
$$\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& \frac{-2}{f-n}& -\frac{f+n}{f-n}\\ 0& 0& 0& 1\end{array}\right]$$
(OpenGL Orthographic Projection Matrix)
如果观察参数都是对称的这个矩阵还可以更简单(r=-l,t=-b);
$\{\begin{array}{l}r+l=0\\ r-l=2r(width)\end{array},\{\begin{array}{l}t+b=0\\ t-b=2t(height)\end{array}$
$$\left[\begin{array}{cccc}\frac{1}{r}& 0& 0& 0\\ 0& \frac{1}{t}& 0& 0\\ 0& 0& \frac{-2}{f-n}& -\frac{f+n}{f-n}\\ 0& 0& 0& 1\end{array}\right]$$