二分查找及二分答案

一、二分思想

二分是一种常用且非常精妙的算法，常常是我们解答问题的突破口，二分的基本用途是在单调序列或单调函数中做查找操作，因此当问题的答案具有单调性时，就可以通过二分把求解转化为判定(根据复杂度理论，可知判定的难度小于求解)，这使得二分的应用范围变得很广泛。

二分的关键是边界，而不是单调性，所以，小白学习二分一定要注意边界问题。

二、二分查找

线性查找需要从头开始不断地按顺序检查数据，因此在数据量大且目标数据靠后，或者目标数据不存在时，比较的次数就会更多，也更为耗时。若数据量为 n，线性查找的时间复杂度便为 O(n)。

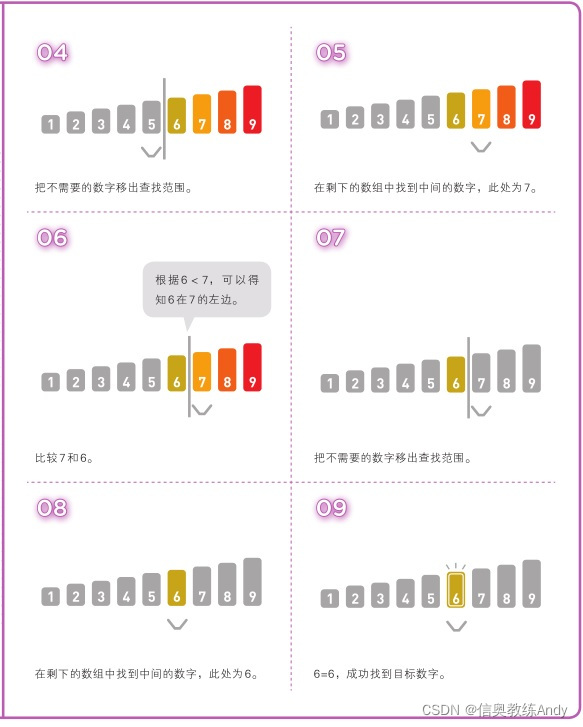
二分查找只能查找已经排好序的数据。二分查找通过比较数组中间的数据与目标数据的大小，可以得知目标数据是在数组的左边还是右边。因此，比较一次就可以把查找范围缩小一半。重复执行该操作就可以找到目标数据，或得出目标数据不存在的结论。

下面看图说话

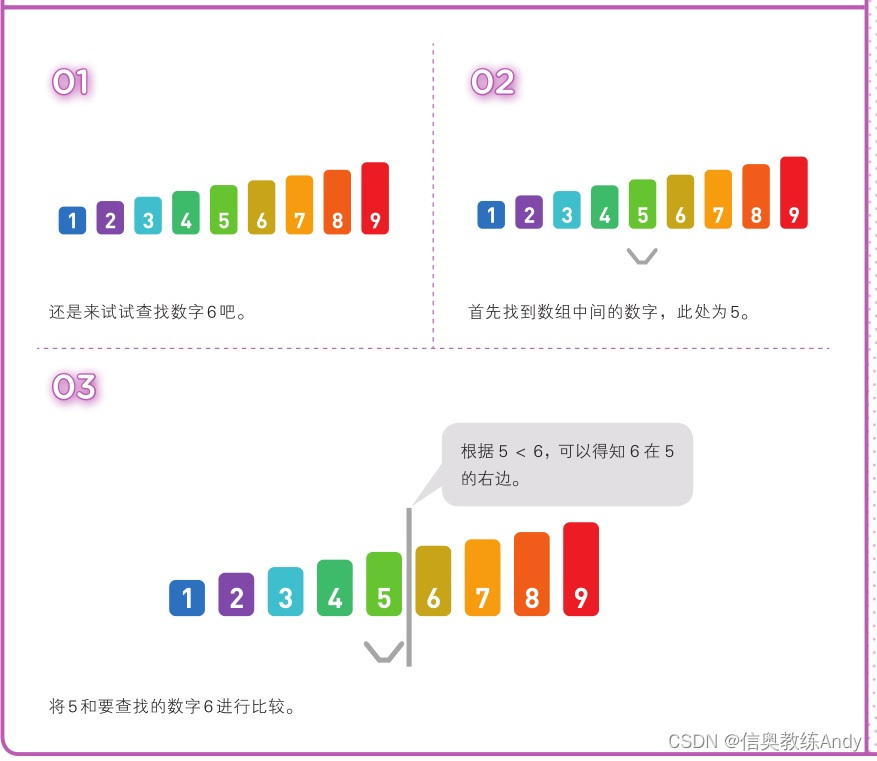
 因为每次都可以将区间大小缩小一半，所以最多只需要 log(n) 次就可完成查 找，所以二分查找的复杂度是 O(log(n)) 

二（1）整数二分查找模版

int find(int x)
{
	int l = 1;
	int r=n+1;//左闭右开的区间哦
	while(l<r)
	{
		int mid = (l+r)/2;//l+(r-l)>>1这样可以避免越界
		if(a[mid]>=x)
			r=mid;
		else l=mid+1;
	}
	if(a[l]==x) return 1;
	else return -1;
}

二（2）实数域二分

int Erfen( double l, double r)
{∥dlt=0.001(根据题目要求决定精度)
double mid;
while(fabs(l-r)>dlt)
{
mid=(l+r)/2.0;
if( check(mid))r=mid;
else l=mid;
}
return l;
};

如上所述，如果我们指定二分的次数t，那么对于初始的求解区间长度L，算法结束后r-1的值会是L/2^t，根据这个值判断精度是否达到我们的要求即可 。

二（3）STL中的二分查找

1、upper_bound  

upper_bound(begin,end,num)会从数组的begin 位置到end−1 位置二分查找第一个大于 num的数字的位置（最终返回的是一个地址，即第一个大于num的数字的位置，如果不存在则返回-1。通过返回的地址减去起始地址 ，得到找到数字在数组中的下标。）

#include<bits/stdc++.h>

using namespace std;

int main(){  

int num[6]={1,2,4,7,15,34};

sort(num, num + 6); //按从小到大排序

int pos = upper_bound(num, num + 6, 7) - num; //返回数组中第一个大于或等于被查数的值

cout << pos << " " << num[pos] << endl;

return 0;

}

输出：4 15

2、lower_bound

lower_bound(begin,end,num) 会从数组的begin 位置到end-1 位置二分查找第一个大于或等于num的数字的位置

#include<bits/stdc++.h>

using namespace std;

int main(){

int num[6] = {1, 2, 4, 7, 15, 34};

sort(num, num + 6); //按从小到大排序  

int pos = lower_bound(num, num + 6, 7) - num; //返回数组中第一个大于或等于被查数的值

cout << pos << " " << num[pos] << endl;

return 0;

}

输出结果：3 7

三、二分答案

当问题的答案具有单调性时，就可以通过二分把求解转化为判定(根据复杂度理论，可知判定的难度小于求解)

第一种写法：左闭右开区间写法：[l,r)，循环l=r结束。

每次二分的中间值mid会归属于左半段与右半段二者之一。

1. 在单调递增序列a中查找>=x的数中最小的一个（即x或x的后继）：

   while(l<r)
   {
   int  mid = (l+r)>>1;//mid=l+(r-l)/2;//>>向下取整，整除是向零取整
   if(check(mid)) r=mid;//a[mid]>=x
   else l=mid+1;
   }
   return a[l];

• 在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）:

  while(l<r)
  {
  int  mid = (l+r+1)>>1;
  if(check(mid)) l=mid;//a[mid]<=x
  else r=mid-1;
  }
  return a[l];

  为什么需要+1？
  原因是如果不加上1，那么mid得到的是下取整的数，那么有可能[mid,r]更新过后mid会一直等于mid（mid==r的情况）会陷入死循环左闭右闭的写法，[l,r]

• 第二种写法，[l,r]写法

• 最小值最大(或是最大值最小)问题，这类双最值问题常常选用二分法求解，也就是确定答案后，配合贪心、DP等其他算法检验这个答案是否合理，将最优化问题转换为判定性问题。

1. 

当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。  

• 

        当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。 

例题讲解： 

 例1：查找

例2：眼红的Medusa

例3： 击进的奶牛

例4：数列分段