堆排序—数组中的第K个最大元素

堆

堆可以看作是一个近似的完全二叉树；

完全二叉树？？

完全二叉树就是对于一颗二叉树，假设深度为d，除第d层外的所有节点都构成满二叉树，且第d层所有节点从左到右连续紧密排列；

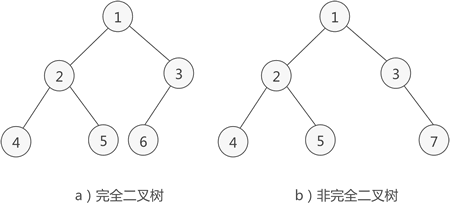
满二叉树？？

满二叉树就是叶子节点都在同一层，并且除了叶子节点之外的节点都有两个子节点；

堆可分为 最大堆 和 最小堆；最大堆就是根节点是最大元素，除了根节点，其他节点最多和其父节点一样大；左右兄弟之间没有顺序；

十大排序算法中的堆排序中，通常使用最大堆进行排序；最小堆通常用于构造优先队列；

最大堆-堆排序

最大堆的特点就是根节点是最大元素，因此利用最大堆排序就要时刻维护这个最大堆；

如果你想求出一个数组的最大值，那就直接将这个数组最大堆化，nums[0](即根节点就是最大值)；如果你先求出第K大的数，那就不停将根节点移除，将其余数进行最大堆化，这样反复执行K次，那就得到了我们想要的第K大的元素；

例题

Leetcode 中关于堆排序的就有 数组中的第K个最大元素；这道题也是面试中最常问的问题，变相的考察了排序算法；

如何排序

假设已经有一个"堆"了，但是顺序不对，因此需要对它进行堆化；

堆化

void heapify(vector<int>& nums,int len,int parent) {
    if(parent >= len) return;

    int left = parent*2+1;
    int right = parent*2+2;
    int max = parent;

    if(left < len && nums[left] > nums[max]) max = left;
    if(right < len && nums[right] > nums[max]) max = right;
    if(max != parent) {
        swap(nums[max],nums[parent]);
        heapify(nums,len,max);
    }
}

在堆化之前尼，我们就需要知道哪些节点需要调整；例如，对最深一层的叶子叶子节点，我们就没有必要对它进行排序，因为它就没子节点啊；知道哪些节点需要去调整，也就是一个建堆的过程；

建堆

void buildHeap(vector<int>& nums,int len) {
    int parent = (len-2)/2;
    for(int i = parent; i >= 0; --i) {
        heapify(nums,len,i);
    }
}

• 通过叶子节点的父节点就可以查询到子节点的值，因此，我们只需要从最后一个父节点开始遍历；

找第K大值

int findKthLargest(vector<int>& nums, int k) {
    int len = nums.size();
    buildHeap(nums,len);

    for(int i = len-1; i >= len-k+1; --i) {
        swap(nums[0],nums[i]);
        heapify(nums,i,0);
    }
    return nums[0];
}