平衡二叉树（AVL tree）概述

一、AVL tree基本概念

AVL树前提是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1。

平衡因子BF（balance Factor）：二叉树结点的左子树深度与右子树深度的值，AVL树上所有节点的BF只能是-1、0、1，如果二叉树上有一个节点的BF的绝对值大于1，那么这个二叉树就是不平衡的。

最小不平衡子树：距离插入节点最近的，且平衡因子的绝对值大于1的结点为根的子树，被称为最小不平衡子树。

二、AVL树的构建步骤

数组a[10]={3,2,1,4,5,6,7,10,9,8},构建AVL树的过程：

对于前3位3、2、1，当3的BF为2（正），将整个树进行右旋（顺时针旋转）：

增加结点4后，如图3，平衡因子没发生改变。在增加结点5，结点3的BF值为-2（负），对这颗最小平衡子树进行左旋（逆时针旋转）。

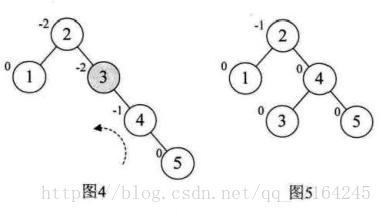
增加结点6之后，结点2的BF变为-2，要进行左旋，注意结点3的变化，从结点4的左孩子变为结点2的右孩子：