主成分分析（PCA）（principal component analysis）

大豆木南

已于 2023-06-09 17:06:10 修改

阅读量3.2k

点赞数 3

CC 4.0 BY-SA版权

分类专栏：人工智能机器学习自然语言处理文章标签：线性代数 pca降维机器学习算法

于 2021-10-03 17:12:13 首次发布

本文链接：https://blog.youkuaiyun.com/qq_32103261/article/details/120592736

本文主要讲PCA的相关数学推导。PCA的数学推导用线性代数的知识就可以完成。

参考deeplearningbook.org一书2.12 Example: Principal Components Analysis

参考李航统计学习方法第16章主成分分析

本文的目录如下：

我们先讲两个用到的线性代数知识点：

用到的知识点

1、矩阵对角线元素之和（the trace operator）

矩阵对角线元素之和（the trace operator）,记做 Tr ，定义如下：

它有如下的性质：

1一个矩阵的trace等于它的转置的trace

2 循环置换性

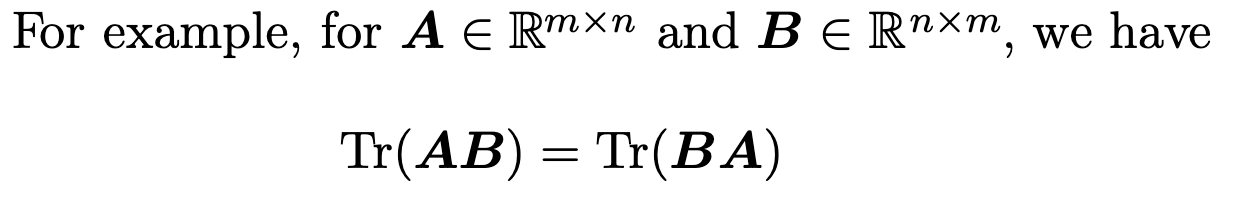
2、矩阵的 Frobenius norm ：

它有如下的性质：

好啦，两个小知识点说完，就开始PCA啦～

PCA 数学推导

我们有 $\mathbb{R}^{n}$ 空间上的 m 个点 $\{\boldsymbol{x}^{(1)},\boldsymbol{x}^{(2)},\cdot \cdot \cdot ,\boldsymbol{x}^{(m)} \}$ ，每一个点都是 n 维的向量。我们把这些点存起来，要用 $m\times n$ 个单位内存空间，如果我们空间有限，能不能用更少的空间存储和原来差不多的信息，使得信息减少尽可能的小。一个方法就是降维，对于每个点 $\boldsymbol{x}^{(i)}\in \mathbb{R}^{n}$ ，我们找到这个点对应的的 $\boldsymbol{c}^{(i)}\in \mathbb{R}^{l}$ ，并且 $l < n$ ，这样就可以减少原始数据的存储空间，用数学表达式表示出来就是 $f(\boldsymbol{x})=\boldsymbol{c}$ ， $\boldsymbol{x}\approx g(f(\boldsymbol{x}))$ ，这里的 $\boldsymbol{x}$ 指 $\boldsymbol{x}^{(i)}$ ， $c$ 指 $\boldsymbol{c}^{(i)}$ ，为了看着方便，我们后边就用 $\boldsymbol{x}$ 和 $\boldsymbol{c}$ 表示任意点的原始向量和降维之后的向量， $f$ 函数是编码函数（encoding function）， $g$ 函数是解编码函数（decoding function）。（为什么要用解码函数呢？因为 $\boldsymbol{x}$ 是 $n$ 维向量， $\boldsymbol{c}$ 是 $l$ 维向量，不同维度的向量无法比较）

PCA就是提供了这样一种降维的方法。

开始正式推导啦～

PCA的推导先从解编码函数说起，为了使解编码函数尽可能简单，可以选择矩阵相乘的方式使得 $g(\boldsymbol{c})=\boldsymbol{D}\boldsymbol{c}$ ，其中 $\boldsymbol{D}\in \mathbb{R}^{n\times l}$ 。如果不做任何限制，计算最优的 $\boldsymbol{D}$ 比较困难，所以对 $\boldsymbol{D}$ 做一些限制的话看看能不能得到我们想要的效果。事实上我们可以假设 $\boldsymbol{D}$ 的每一列之间都是正交的，（此时的 $\boldsymbol{D}$ 还不是正交矩阵，因为 $l\neq n$ ）。为了使编码后的向量唯一，限制 $\boldsymbol{D}$ 的每一列向量都是单位向量。对 $\boldsymbol{D}$ 做了这个限制后计算最优的 $\boldsymbol{D}$ 就比原来简单很多。