排序（左神初级）p2

前言：荷兰国旗问题(leetcode颜色分类)

给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N).

这个问题已经描述的很清楚了，其思想就是设置左l、右r、当前cur三个指针，分别指向小于num的最后一个元素位置、小于num的最后一个元素位置、当前元素。

若当前指向的元素小于num，则放置到左边，与l指针的后一个位置交换，l++、cur++，这里cur++是因为cur之前元素已经扫描过了；

若等于num则跳过，cur++；

若大于num，则放置到右边，与r指针的前一个位置交换，并判断当前cur的值；

直至cur指针与r发生碰撞。

class Solution {
public:
    void sortColors(vector<int>& nums) {
        quick(nums,0,nums.size()-1,1);
    }
    void quick(vector<int>& nums,int l,int r,int num){
         int p1=l-1;
         int p2=r+1;
         int cur=l;
         while(cur<p2){
             if(nums[cur]<num){
                 swap(nums[cur++],nums[++p1]);
             }else if(nums[cur]>num){
                 swap(nums[cur],nums[--p2]);
             }else
             cur++;
         }
    }
};

---

1.快速排序

优化快排（三指针分区）：本质是一个荷兰国旗问题

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
      quicksoret(nums,0,nums.size()-1);
      return nums;
    }
 //荷兰国旗问题，只不过以最后一个值nums[r]为基准
    vector<int> partition(vector<int>& nums,int l,int r){
        int less=l-1;
        int more=r;
        while(l<more){
            if(nums[l]<nums[r]){
                swap(nums[l++],nums[++less]);
            }
            else if(nums[l]>nums[r]){
                swap(nums[l],nums[--more]);
            }else
            l++;
        }
      //最后需要交换nums[r]元素
        swap(nums[more],nums[r]);
       vector<int> p(2);
       p[0]=less+1;
       p[1]=more;
       return p;
    }

    void quicksoret(vector<int>& nums,int l,int r){
        if(l<r){
            vector<int> mid=partition(nums,l,r);

            quicksoret(nums,l,mid[0]-1);
            quicksoret(nums,mid[1]+1,r);
        }
    }
};

随机快排：只需要将最后一个元素和中间任意一个元素交换：

    void quicksoret(vector<int>& nums,int l,int r){
        if(l<r){
   //rand()%m+n;生成m-（m+n-1）的随机数
            int i = (rand() % (r - l + 1)) + l;
            swap(nums[i],nums[r]);
            vector<int> mid=partition(nums,l,r);

            quicksoret(nums,l,mid[0]-1);
            quicksoret(nums,mid[1]+1,r);
        }
    }

经典快排：双向扫描分区法，固定最后一个元素

                     

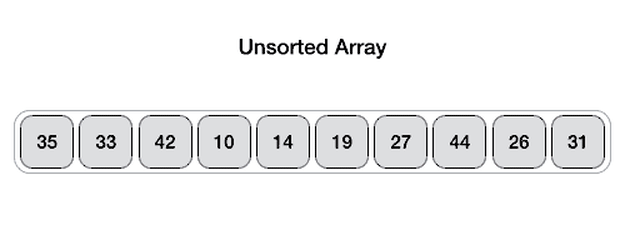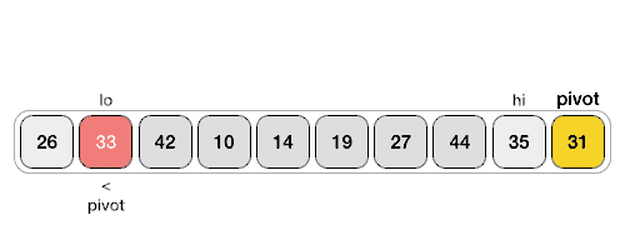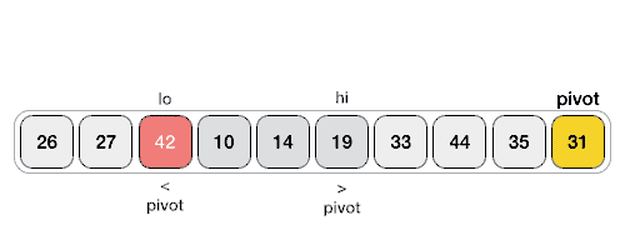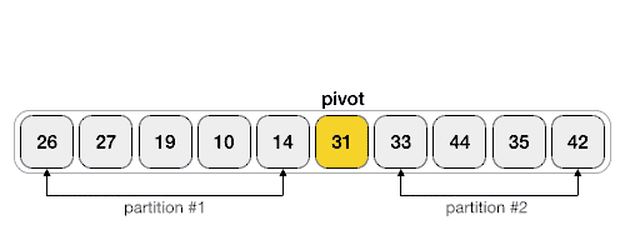
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
      quicksoret(nums,0,nums.size()-1);
      return nums;
    }
    int partition(vector<int>& nums,int l,int r){
     
        int i = l , j = r-1;
     //一定是while （true）
		while (true)
		{
			while (i <= j && nums[i] <= nums[r]) i++;
			while (i <= j && nums[j] >= nums[r]) j--;
			if(i>j) break;
			swap(nums[i], nums[j]);
		}
		swap(nums[i], nums[r]);
		return i;
    }

    void quicksoret(vector<int>& nums,int l,int r){
        if(l<r){
            int i = (rand() % (r - l + 1)) + l;
            swap(nums[i],nums[r]);
            int mid=partition(nums,l,r);

            quicksoret(nums,l,mid-1);
            quicksoret(nums,mid+1,r);
        }
    }
};

---

2.堆排序

堆，是一个完全二叉树，一个节点i的左右孩子节点为：2i+1、2I+2，父节点为(i-1)/2。

堆排序首先需要建立大根堆或者小根堆，其次需要插入操作，还需要写某一个值变小下沉的操作。

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for(int i=0;i<nums.size();i++){
            heapinsert(nums,i);
        }
        int heapsize=nums.size();

       //交换[0]位置元素和最后一个位置元素，对[0]位置进行heapify
        swap(nums[0],nums[--heapsize]);
        while(heapsize>0){
            heapify(nums,0,heapsize);
            swap(nums[0],nums[--heapsize]);
        }
        return nums;
    }

    //建立大根堆
    void heapinsert(vector<int>& nums,int index){
        while(nums[index] > nums[(index-1)/2]){
            swap(nums[index] , nums[(index-1)/2]);
            index=(index-1)/2;
        }
    }

    //某值变小的下沉操作
    void heapify(vector<int>& nums, int index, int heapsize){
      int left=index*2+1,large;
      while(left < heapsize){
           if(left+1<heapsize && nums[left+1]>nums[left])large=left+1;
              else large=left;
           if(nums[large]<=nums[index])break;
           if(nums[large]>nums[index]) swap(nums[large],nums[index]);

           index=large;
           left=index*2+1;
      }
    }
};

扩展：数据流的中位数

class MedianFinder {
public:
    int size;
    priority_queue<int> max;
    priority_queue<int , vector<int>, greater<int>> min;
    /** initialize your data structure here. */
    MedianFinder() {
      size=0;
    }
    
    void addNum(int num) {
          size++;
          min.push(num);
          max.push(min.top());
          min.pop();

          if(max.size()>max.size()) {
              max.push(min.top());
              min.pop();
          }
    }
    
    double findMedian() {
         if(size == 0) return -1;
        if(size % 2) return min.top();
        else return 0.5 * (max.top() + min.top() );
    }
};

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */