ABC-Net:Towards Accurate Binary Convolutional Neural Network 论文学习

冰激凌很菜

已于 2022-03-29 15:46:10 修改

阅读量2.5k

点赞数

分类专栏：神经网络量化文章标签：深度学习神经网络人工智能

于 2022-03-28 18:52:42 首次发布

本文链接：https://blog.youkuaiyun.com/qq_31993233/article/details/123800362

版权

神经网络量化专栏收录该内容

11 篇文章

订阅专栏

论文连接：https://proceedings.neurips.cc/paper/2017/hash/b1a59b315fc9a3002ce38bbe070ec3f5-Abstract.html

摘要

我们引入了一种新的方案来训练二进制卷积神经网络(CNNs)-在运行时的权重和激活限制为{-1，+1}。众所周知，使用二进制权值和激活可以大大减少内存大小和访问，并可以用更有效的按位操作取代算术操作，从而导致更快的测试时间推断和更低的功耗。然而，以往对二元cnn进行二值化的研究通常会导致严重的预测精度下降。在本文中，我们用两个主要的创新来解决这个问题：（1）用多个二值权值基的线性组合逼近全精度权值；（2）使用多个二进制激活来减轻信息损失。得到的二进制CNN的实现，记为ABC-Net，被证明具有更接近全精度的性能，在有足够的二值权重基础和激活的情况下，甚至在ImageNet和森林跟踪数据集上达到相当的预测精度。

3. 二值化方法

在本节中，我们将详细说明我们的二值化方法，为了方便起见，该方法被称为ABC-Net（精确-二值化卷积）。请记住，在训练过程中，实值权值在每个历元中都被保留和更新，而在测试过程中，在卷积中只使用二进制权值。

3.1 权重近似

考虑一个L层CNN架构。我们提出了每一层权值的两种二值化方法：1)整体近似权值（per-layer）和 2)通道近似权值(per-channel)。

3.1.1 整体近似权值

整体权重近似
在量化公式上做如下修改:这是基于观察到全精度权值倾向于对称，非稀疏分布，接近高斯分布。好处在讨论部分有。
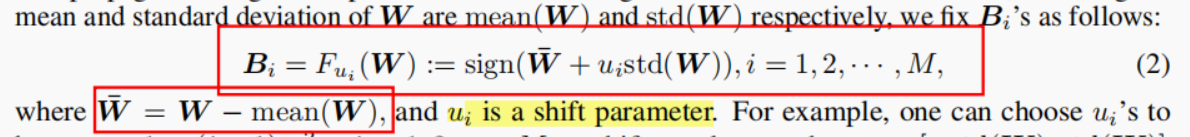
在这里插入图片描述

正向反向传播

ABC-Net结构

3.1.2 通道近似权值(per-channel)

通道近似权值(per-channel)
与整体上的权值近似相比，通道式方法更详细地逼近权值，但在推理过程中不需要额外的成本。由于这种方法在训练过程中需要更多的计算资源，我们将其作为未来的工作，并在本文中关注前一种近似方法。

3.2 多个二进制激活和位操作卷积

激活值的量化
卷积操作

3.3 训练算法

一般卷积包括：1conv，2.BN, 3.activation 4. polling,但是很多研究发现polling在最后会引起精度掉很懂。因为我们调整为：1conv，2. polling 3.BN, 4.activation

由于我们的二值化方案近似于全精度的权值，因此使用全精度的训练前模型可以作为一个初始化网络。然而，对于权重总是需要进行微调，以适应新的网络结构。

4. 实验结果

ImageNet
不同 1 bit 个数配置的A W对精度影响
M,N代表weight 和activate的个数（不是bit数）
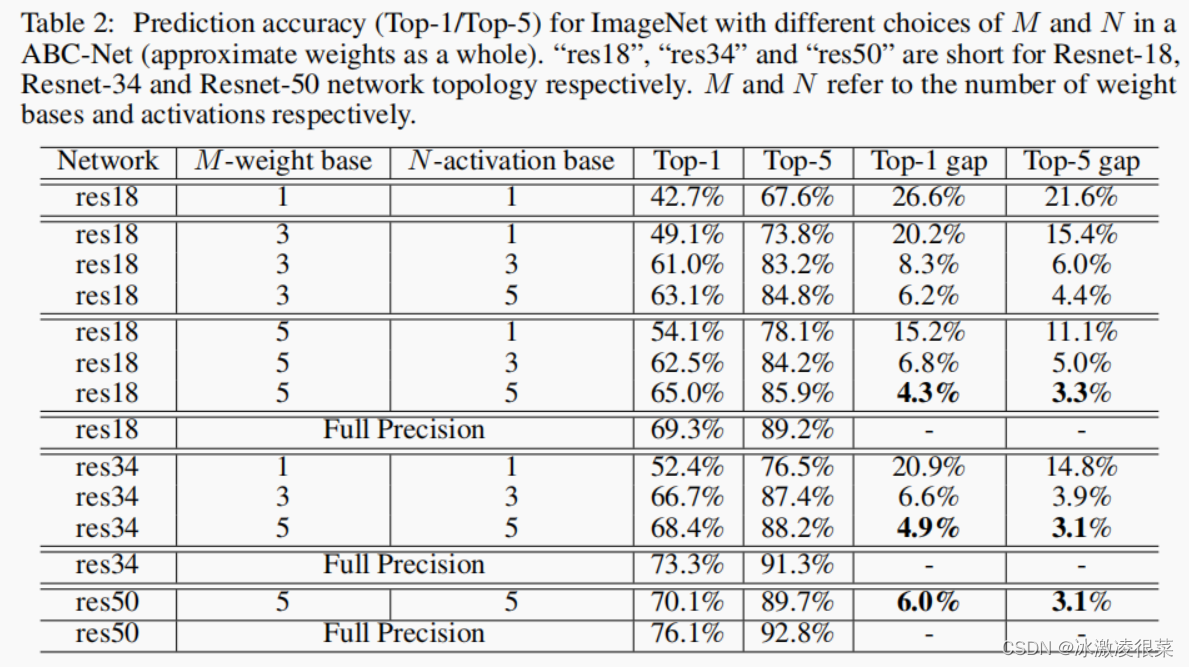
不同配置的A W对精度影响
Comparison with the state-of-the-art
有人可能会说，5位宽度的量化方案可以达到与ABCNet相似的5个权重基和5个二元激活的精度。然而，前者的效率较低，并且需要明显更多的硬件资源。

5. 讨论

5.1 为什么在参数中加入位移

直观地说，多重二值化的权重基/激活方案是有效的，因为它允许更多的信息传递。考虑一个实值，比如1.5，被传递给一个二值化函数f(x)=sign(x)，其中符号将一个正的x映射到1，否则为-1。在这种情况下，f（1.5）的输出为1，这表明输入值是正的。现在假设我们有两个二值化函数f1(x)=sign(x)和f2(x)=sign(x−2)。在这种情况下，f1输出1和f2输出-1，这表明输入值不仅为正，而且必须小于2。很明显，我们可以看到每个函数对表示输入的贡献都不同，与前一种情况相比，从f2中获得了更多的信息。

从另一个角度来看，系数（β）和移位参数都有望学习和利用全精度张量的统计特征，就像批归一化中的尺度和移位参数一样。如果我们有更多的二值化权值基/激活，网络就有能力更精确地近似全精度的一个。因此，可以推断，当M或N足够大时，网络学会调整自己，使M个权重基或N个二值化激活的组合可以像全精度激活一样。

5.2 相对与Nbit定点方案的有点

具体来说，我们的K个二值化的权值基/激活值更优于固定的K位宽度方案，原因如下：
（1）K个1bit数运算肯定是比1个Kbit 数运算更简单的，因为他保留了BNN或者XNOR-Net 直接XNOR以及popcount的优点.
(2)在数字芯片中，K位宽度乘法器比K个1位乘法器消耗更多的资源：
它需要超过K位来存储和计算，否则它很容易溢出/下流。例如，如果一个实数被量化为一个2位数，那么一个可能的选择就在{0、1、2、4}的范围内。在这个2位乘法中，当两个数字都是4时，它输出4⇥4=16，这不在范围内。乘数的复杂性与位宽的平方成正比。相比之下，我们的K二值化方案没有这个问题——它总是输出在{-1,1}的范围内。节省下来的硬件资源可以进一步用于并行计算。
（3）二进制激活可以使用峰值响应进行基于事件的计算和通信（仅在必要时消耗能量），因此是节能的。这可以在我们的方案中使用，但不能在固定的k位宽度方案中使用。

5.3 讨论推理过程减少计算的方式

（1）关于移位操作
在这里插入图片描述

（2）关于BN
在这里插入图片描述

6. 总结

我们引入了一种新的二值化方案，用于正向和反向传播期间的权值和激活，称为ABC-Net。我们已经证明了在ImageNet上用ABC-Net训练一个二元CNN是可能的，并达到接近其全精度对应的精度。本工作中提出的二值化方案是可并行的和硬件友好的，这种方法对cnn的特殊硬件实现，对卷积的影响可能是重大的。加速测试时间推断的潜力可能对实时嵌入系统非常有用。未来的工作包括将这些结果扩展到其他任务，如对象检测和其他模型，如RNN。此外，研究使用FPGA/ASIC或其他定制的深度学习处理器[Liu等人，2016]在运行时实现ABC-Net也是很有趣的。