[图形学]Delaunay三角剖分算法附C++实现

完整代码已上传：点击此处

将离散点构成三角网，这种三角网称为Delaunay三角网

Delaunay剖分具备的优异特性有（来自百度百科）：

1.最接近：以最近的三点形成三角形，且各线段(三角形的边)皆不相交。

2.唯一性：不论从区域何处开始构建，最终都将得到一致的结果。

3.最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小的角度不会变大。

4.最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大。

5.区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。

6.具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

首先看我的程序结果（演示程序已上传）：

 

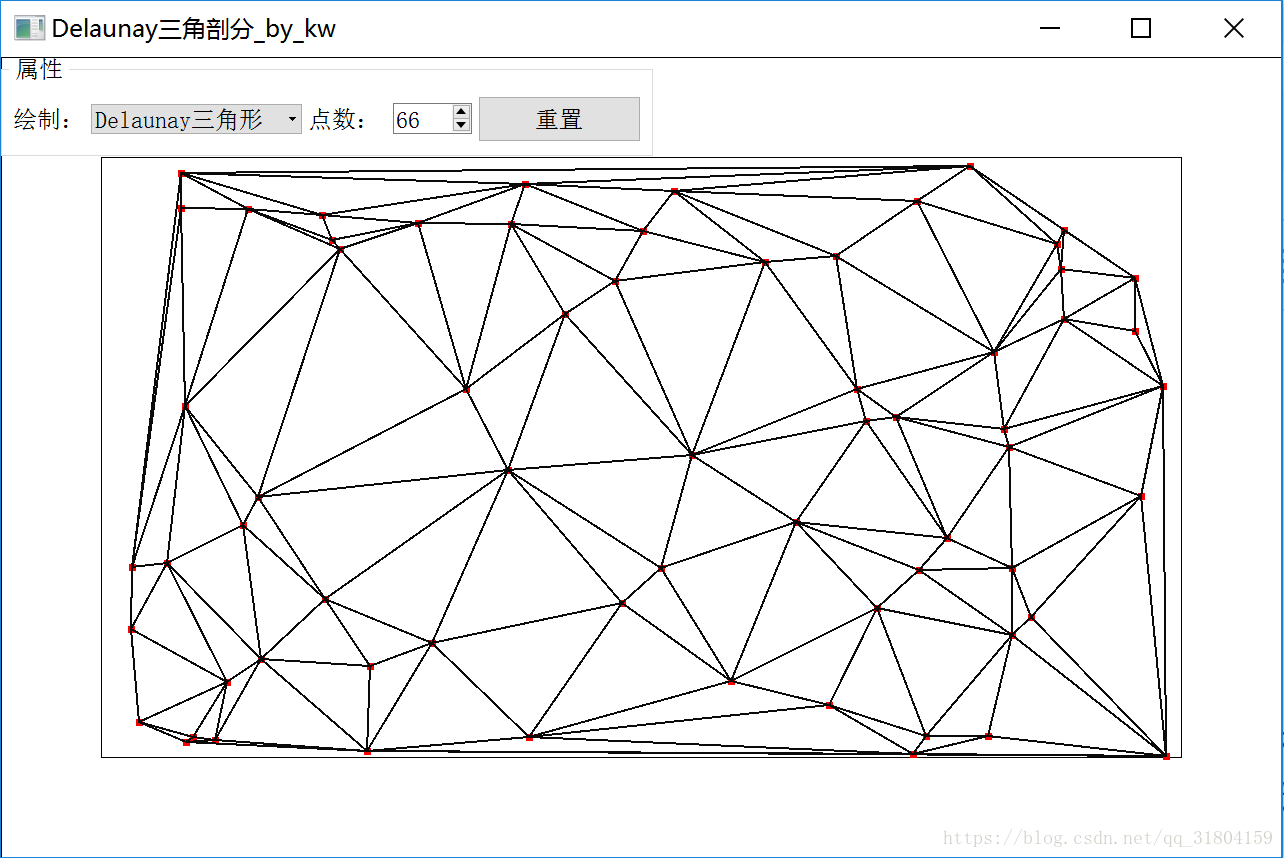
下面介绍D