区间估计的练习题

本博客根据非常好的excel资料而编写，使用python语言操作，预计使用一周的时间更新完成。需要《非常好的excel资料》word文档，欢迎发邮件给1982500361@qq.com，免费发放。这篇博客对应《非常好的excel资料》里的第2章节的练习题。
4.6 练习题
（通过调用以上函数就可解决）
题目：某类树种的树高符合正态分布，随机抽60个样本数，试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.
① 分析：可见其方差未知，求均值的置信区间，于是使用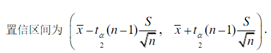

②代码

tree=pd.read_csv('D:\data.csv',encoding='gbk')
tree=tree['高度']
mean = tree.mean() 
std = tree.std()
def wucha3(a,s,n):
    return np.abs(a*s/np.sqrt(n))
def gujiqujian3(a,s,n,mean):
    cha=wucha2(t.ppf(1-a/2,n-1),s,n)
    print('[',mean-cha,mean+cha,']')

③ 结果图

2、题目：随机抽十个样本，试求总体方差的0.9的置信区间(设总体为正态).
①分析：即均值未知时求方差的置信区间，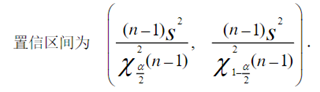
②代码

dataex23=pd.read_csv('D:\ex23.csv',encoding='gbk')
dataex232=dataex23['灯泡寿命']
def Han(n,s,a):
    y1=chi2.ppf(1-(1-a)/2,n-1)
    y2=chi2.ppf(1-(1-(1-a)/2),n-1)
    x=(n-1)*s**2
    print('[',x/y1,x/y2,']')

③结果图

3、题目：玉米产量符合正态分布，有两个实验区，第一个实验区施磷肥，试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)
① 分析：方差相等但未知，求u1-u2的置信区间
②代码

dataex2321=dataex23['实验区1']
dataex2322=dataex23['实验区2']
mean2331 = dataex2321.mean()
mean2332 = dataex2322.mean()
var2331 = dataex2321.var()
var2332 = dataex2322.var()
count2331 = dataex2321.count()
count2332 = dataex2322.count()
count233 = count2331 + count2332-2
mean233 = mean2331 - mean2332
def gujiqujian4(a,count,count11,count12,var11,var12,mean):
    tt=t.ppf(1-a/2/2,10)#t0.05 (10) 临界值
    s = np.sqrt(((count11-1)*var11+(count12-1)*var12)/count)*np.sqrt(1/count11+1/count12)
    print('[',mean-tt*s,mean+tt*s,']')

④ 结果图

下一个博客：假设检验实验
上一个博客：区间估计