Leetcode K-th Smallest in Lexicographical Order详解

原创于 2019-05-27 19:24:29 发布 · 624 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#树 #先序遍历 #第k小的数 #leetcode

leetcode 同时被 2 个专栏收录

36 篇文章

订阅专栏

树

2 篇文章

订阅专栏

该博客详细解析了LeetCode 440题，通过将问题转化为树的先序遍历来寻找字典序第k小的数字。文章介绍了如何构建解决方案，包括计算相邻节点之间的步数以及如何有效地移动到目标节点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

440. K-th Smallest in Lexicographical Order

Description:

Given integers n and k, find the lexicographically k-th smallest integer in the range from 1 to n.

Note: 1 ≤ k ≤ n ≤ 109.

Example:

Input:
n: 13   k: 2

Output:
10

Explanation:
The lexicographical order is [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9], so the second smallest number is 10.

解答

这道题一上来可能没思路，仔细想一下发现lexicographical order可以转化为树的先序遍历来做。
具体转化过程如下:

树结构

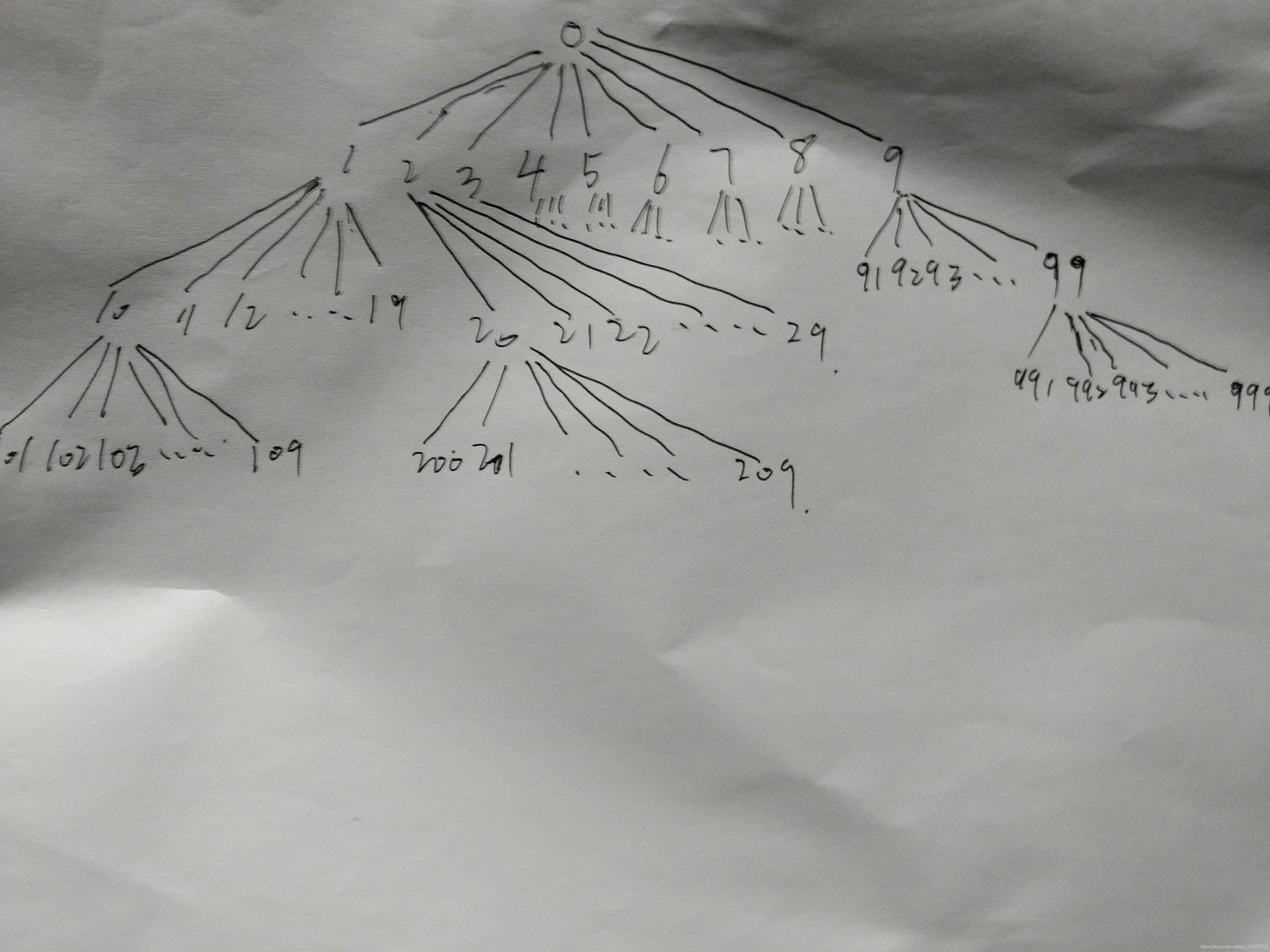
求第k小的数即是求树的先序遍历的第k个节点的值，我们可以直接构建一个树，但是这样太麻烦。

我们的目标是从第1个节点开始，移动k - 1 步到目标节点。

为了减少移动次数，我们先计算同一level的邻居节点之间的步数以跳过不必要的先序遍历。
比如说假设n为20，k为12，我们一开始处于节点1，我们先计算节点1和2之间的步数（1和2之间有11步），然后令k = k - 11就可以直接跳到节点2，此时k为1，输出节点2的值。

所以总体思路是：假设我们处于cur节点上，我们先计算同一level的邻居节点之间的步数steps，如果steps小于k，我们跳到邻居节点cur + 1，然后令k -= steps,当steps大于等于k时，我们进入树的下一层，然后用同样的方法计算，最终到达目标节点。

那么我们如何计算节点之间的步数呢，假设第一个节点是now，邻居节点是next,当next <= n时，我们就把同一level从now 到next之间的节点数量加上来，如果 next > n，我们就把now到n（包括n）之间的节点数量加上来，然后进入树的下一层重复刚刚的操作。

代码


class Solution {
public:
    long findKthNumber(int n, int k) {
        long cur = 1;
        
        while (k > 1) {
            long steps = calcSteps(cur, cur + 1, n);
            if (steps < k) {
                cur += 1;
                k -= steps;
            }
            else {
                k -= 1;
                cur *= 10;
            }

        }
        return cur;

    }

    long calcSteps(long now, long next, long n) {
        long steps = 0;
        while (now <= n) {

            steps += min(n + 1, next) - now;
            next *= 10;
            now *= 10;

        }
        return steps;
    }
};