基于 Java 机器学习自学笔记（第75-76天：通用化BP神经网络: 单层神经网络封装与总体组合）-优快云博客

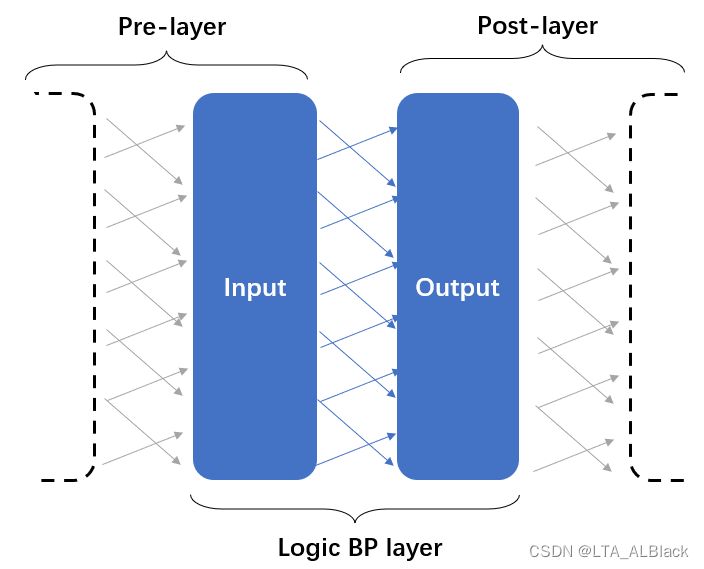
因此我计划将单层的BP神经网络的类封装为以" 逻辑输入部分 "为基础, 以" 逻辑输出部分 " 为辅助的的数据结构. 这里的输入输出并不是全局意义的输入或输出层, 而是在数据流进入单层逻辑BP层数据结构后, 输入层用于存储我们数据的输入, 并且在逻辑上代表本层. 而输出部分则用于存放进行若干操作后用于留以后续对象可以读取的中转结构. 值得注意的是, 当前逻辑BP层拥有的辅助输出部分, 在进入下一个逻辑BP层后将会变成主要的输入部分(这个详细可见上图).

1.2 体现forward的抽象与变量

forward在BP逻辑层的抽象如上, numInput用于表明输入部分的结点数, 其数目用于事实上表明当前逻辑层的结点数. numOutput用于表明输出部分的结点数, 其数目需要与下一个逻辑BP层的输入层一致. 就像连接两个设备的中转线, 要保证接口的适配. input[ ]与output[ ]分别是其表示的数组, 用于存储forward过程中存储的预测值.

此外, 本代码计划设计一个activitedOutput[ ]数组用于保存通过激活函数得到的\(y\)值而不去专门覆盖output[ ]内的属于激活函数内变量\(x\)的内容. 这个操作在我的那篇关于BP概念的文章中并没有体现, 这是因为那篇文章采用的Sigmoid激活函数在求导之后得到的隐函数中并没有自变量\(x\), 因此没必要保留激活函数的输入参数\(x\). 但是在设计如今这种通用性的代码中必须要给backPropagation操作留有余地, 毕竟还是有很多激活函数的求导算式有\(x\).

	/**
	 * The inputs.
	 */
	double[] input;

	/**
	 * The outputs.
	 */
	double[] output;

	/**
	 * The output after activate.
	 */
	double[] activatedOutput;

	/**
	 * The inputs.
	 */
	Activator activator;

	/**
	 * The weight matrix.
	 */
	double[][] weights;

    /**
	 * The number of input.
	 */
	int numInput;

	/**
	 * The number of output.
	 */
	int numOutput;

1.3 体现backPropagation的抽象与变量

backPropagation主要干两件事:

反向更新惩罚信息
通过惩罚信息更新边权

而这两件事情之关键在于反向更新惩罚信息. 在进行抽象之前首先让我们观察一下之前博客中展示的backPropagation过程图

这是一个backPropagation的惩罚信息更新流程, 图中红色圈出来就是激活函数的导函数, 而蓝色圈出来的内容是外部参数, 这个参数来自后继层的惩罚信息\(g_j\)与本层的预测参数\(b_i\)通过" 某些手段 "预处理得到, 我们不妨称之为 惩罚处理信息 以区分惩罚信息\(g_j\).\[e_{i} = \operatorname{extParams} \cdot \operatorname{derive}(x,y) \tag{1}\]

若当前层的后继存在一个BP层实体, 那么\(\operatorname{extParams}\)是通过当前后继层惩罚信息与边权做乘积和得到; 若当前层的后继不存在逻辑BP层实体, 那么\(\operatorname{extParams}\)是通过当前层的预测结点值与目标标签值做差得到.

backPropagation的过程一定要在某些地方与forward区分开来, backPropagation并不是在原来forward数据结构的基础上逆向的操作, 而是基于forward的结点为基础(甚至会使用forward的部分信息), 设置部分惩罚结点作为调整. 其中input与output内存储的值本质上都是forward留下的预测值.

明白这个道理之后, 我在过程图上划定了一个区域作为 " 视图 "(视图即是只有这部分的变量是已知的或可以计算得到的), forward中我们将逻辑BP层抽象为两个layer, 在backPropagation亦如是. 要说联系嘛, \(l-1\)是用于存放原属于forward抽象BP层的input[ ]部分, \(l\)是output[ ]部分.

若本回合要知晓\(l\)层的惩罚信息\(e_i\), 我们需要了解什么呢? \(b_i\)作为output[ ]是已知的, 那么最关键的就是要知道图中外部参数2(图中External parameters2), 这样才能通过求导式drive2 * External parameters2 求得本层(output[ ])的惩罚信息Error[ ]. 两种手段:

我们可以默认将External parameters2设置为函数的形参, 作为本层开始时便已知的条件, 将其抽象为paraErrors[ ]数组, 这样就不要在意这样细节要如何实现.
额外存储一个数组保存output[ ]后继层部分的惩罚信息errors[ ](也就是图中的\(\mathbf{g}\)). 然后在本回合的开始, 先通过计算得到External parameters2.

选哪个呢? 只能是第1种. 因为第2种需要已知\(l+1\)层的惩罚信息\(g_j\), 这个当前是不可知; 而且更重要的是: 这部分的计算并不是一致的, 若当前BP逻辑层已经是神经网络的最后一层, 这部分的计算并不是求和. 你当然也可以的专门去用条件语句分类讨论, 但是这似乎有些舍近求远了.

然后怎么更新边权呢. 若本回合要知道\(l\)层向左的出边权值呢? 通过已知公式:\[v_{i h}=v_{i h}+\eta a_{k} e_{i} \tag{2}\]目前我们已知了末端结点\(a_{k}\), 这个结点在我们的" 视图 "内, 属于可知可得. 然后带入\(l\)层的惩罚信息\(e_i\)就可以完成对于\(l\)层的向左出边进行更新.

最后, 当自己获利后, 要为后代考虑. 我们需要考虑为下层提供有效信息. 本层在获取惩罚处理信息时获得了\(l+1\)层的External parameters2, 而本层在结束时也应该向左提供一个External parameters1, 作为面向前导层的接口, 就像链表中的Next一样.

这个过程可以抽象为下面的结构

我们所谓抽象的BP逻辑层只使用了forward的input层, 而output层并没有实际的使用, 因为我们的目标是更新output层的向左出边, 而向左出边的优化公式中并不需要output层结点信息, 所以实际backPropagation模型并不需要output层. 但是我们却需要input的后继层传递的惩罚处理信息paraErrors[ ], 同时input层处理完毕后也需要向左传递本层的惩罚处理信息errors[ ].

惩罚处理信息若来自后继BP逻辑层, 那么这个预处理信息就是后继BP逻辑层的某个结点的惩罚信息同它的所有出边的乘积和\(\sum^{n}_{i=0} v_{ki}e_i\); 如果惩罚处理信息来自目标标签, 那么惩罚处理信息就是目标标签与实际结点信息的差.(可见下图)

(①是当前backPropagation在BP逻辑层的抽象; ②是当前backPropagation抽象部分向后传递的惩罚处理信息, 是前导层的" external parameters "; ③是当前backPropagation接收的来自后继的惩罚处理信息; ④ 是第一个backPropagation的BP逻辑抽象层接收的惩罚处理信息, 因为它没有后继BP层了, 所以这个惩罚处理信息要专门编写)

    /**
     * The mobp.
	 */
	double mobp;

	/**
	 * The weight matrix.
	 */
	double[][] weights;

	/**
	 * The delta weight matrix.
	 */
	double[][] deltaWeights;

	/**
	 * Error on nodes.
	 */
	double[] errors;

	/**
	 * The inputs.
	 */
	Random random = new Random();

1.4 构造函数

	/**
	 *********************
	 * The first constructor.
	 * 
	 * @param paraActivator
	 *            The activator.
	 *********************
	 */
	public AnnLayer(int paraNumInput, int paraNumOutput, char paraActivator,
			double paraLearningRate, double paraMobp) {
		numInput = paraNumInput;
		numOutput = paraNumOutput;
		learningRate = paraLearningRate;
		mobp = paraMobp;

		weights = new double[numInput + 1][numOutput];
		deltaWeights = new double[numInput + 1][numOutput];
		for (int i = 0; i < numInput + 1; i++) {
			for (int j = 0; j < numOutput; j++) {
				weights[i][j] = random.nextDouble();
			} // Of for j
		} // Of for i

		errors = new double[numInput];

		input = new double[numInput];
		output = new double[numOutput];
		activatedOutput = new double[numOutput];

		activator = new Activator(paraActivator);
	}// Of the first constructor

构造函数的初始化与我们介绍BP算法那篇文章中是一致的, 包括这个for循环中关于边权空间的开辟中, 输入端部分给边权+1以修饰哑结点. 另外, errors[ ]是用于向前导层传递本层的错误处理信息, 而本层在backPropagation的代表只有input, 因此errors[ ]空间大小是numInput.

2. BP逻辑层代码

2.1 forward

	/**
	 ********************
	 * Forward prediction.
	 * 
	 * @param paraInput
	 *            The input data of one instance.
	 * @return The data at the output end.
	 ********************
	 */
	public double[] forward(double[] paraInput) {
		//System.out.println("Ann layer forward " + Arrays.toString(paraInput));
		// Copy data.
		for (int i = 0; i < numInput; i++) {
			input[i] = paraInput[i];
		} // Of for i

		// Calculate the weighted sum for each output.
		for (int i = 0; i < numOutput; i++) {
			output[i] = weights[numInput][i];
			for (int j = 0; j < numInput; j++) {
				output[i] += input[j] * weights[j][i];
			} // Of for j

			activatedOutput[i] = activator.activate(output[i]);
		} // Of for i

		return activatedOutput;
	}// Of forward

有了抽象的模型, 代码就变得简单许多. 这里19行对于output部分第\(i\)个元素进行初始化时并不是赋0, 而是优先赋了哑结点指向自己的边weights[numInput][i]. 这个细节需要留意.

2.2 backPropagation

	/**
	 ********************
	 * Back propagation and change the edge weights.
	 * 
	 * @param paraTarget
	 *            For 3-class data, it is [0, 0, 1], [0, 1, 0] or [1, 0, 0].
	 ********************
	 */
	public double[] backPropagation(double[] paraErrors) {
		//Step 1. Adjust the errors.
		for (int i = 0; i < paraErrors.length; i++) {
			paraErrors[i] = activator.derive(output[i], activatedOutput[i]) * paraErrors[i];
		}//Of for i
		
		//Step 2. Compute current errors.
		for (int i = 0; i < numInput; i++) {
			errors[i] = 0;	
			for (int j = 0; j < numOutput; j++) {
				errors[i] += paraErrors[j] * weights[i][j];
				deltaWeights[i][j] = mobp * deltaWeights[i][j]
						+ learningRate * paraErrors[j] * input[i];
				weights[i][j] += deltaWeights[i][j];
			} // Of for j
		} // Of for i

		for (int j = 0; j < numOutput; j++) {
			deltaWeights[numInput][j] = mobp * deltaWeights[numInput][j] + learningRate * paraErrors[j];
			weights[numInput][j] += deltaWeights[numInput][j];
		} // Of for j

		return errors;
	}// Of backPropagation

Step1: 得到后继的BP逻辑层传递过来的惩罚处理信息, 其作为外部参数存在. 这个参数作为惩罚信息公式\(e_{i} = \operatorname{extParams} \cdot \operatorname{derive}(x,y) \) 中的\(\operatorname{extParams}\)部分, step1就是落实这个公式得到\(e_{i}\).
Step2.1: 得到本层的惩罚信息后, 边可以通过基本的权值和得到下一层的(\operatorname{extParams}\)部分, 并在代码最后return这个信息给下一层.
Step2.2: 目前已知当前BP层的forward遗留预测值 - input[ ]; 同时也知道本层的惩罚信息\(e_i\) - paraErrors[ ]; 旧权与旧权变化值也知道 - weight[ ][ ] - deltaWeights[ ][ ]. 于是通过权更新公式\(v_{i h}=v_{i h}+\eta e_{h} x_{i}\)可以算出新的边权(详见我的BP三部曲的概念篇的公式17)
Step3: 单独更新哑结点的边权weights[numInput][ ]

2.3 backPropagation中的初始的惩罚处理信息代码

刚刚在进行backPropagation单层抽象的时候, 提到了串联每个BP逻辑层的关键因子: 惩罚处理信息. 在各层内部之间的惩罚处理信息是通过后继层实现的权值求乘积和得到的, 那么两端怎么办呢? 尾部还好, 毕竟我们的目的是通过惩罚信息更新边权, 执行到(逆向的)尾部无论有没有传递出惩罚信息, 边权肯定能更新好. 但(逆向的)首部问题就大了, (逆向的)首部没有后继传递来的惩罚处理信息, backPropagation抽象的BP逻辑层肯定没法建立. 所以(逆向的)首部的BP逻辑层的backPropagation函数的形参(惩罚处理信息)内容必须要专门编写:

	/**
	 ********************
	 * I am the last layer, set the errors.
	 * 
	 * @param paraTarget
	 *            For 3-class data, it is [0, 0, 1], [0, 1, 0] or [1, 0, 0].
	 ********************
	 */
	public double[] getLastLayerErrors(double[] paraTarget) {
		double[] resultErrors = new double[numOutput];
		for (int i = 0; i < numOutput; i++) {
			resultErrors[i] = (paraTarget[i] - activatedOutput[i]);
		} // Of for i

		return resultErrors;
	}// Of getLastLayerErrors

2.4 封装输出小测

	/**
	 ********************
	 * Show me.
	 ********************
	 */
	public String toString() {
		String resultString = "";
		resultString += "Activator: " + activator;
		resultString += "\r\n weights = " + Arrays.deepToString(weights);
		return resultString;
	}// Of toString

	/**
	 ********************
	 * Unit test.
	 ********************
	 */
	public static void unitTest() {
		AnnLayer tempLayer = new AnnLayer(2, 3, 's', 0.01, 0.1);
		double[] tempInput = { 1, 4 };

		System.out.println(tempLayer);

		double[] labelArray = { 0, 0, 1 };
		double[] tempError = tempLayer.backPropagation(tempLayer.getLastLayerErrors(labelArray));
		System.out.println("Forward, the output is: " + Arrays.toString(tempOutput));

		double[] tempError = tempLayer.backPropagation(tempOutput);
		System.out.println("Back propagation, the error is: " + Arrays.toString(tempError));
	}// Of unitTest

	/**
	 ********************
	 * Test the algorithm.
	 ********************
	 */
	public static void main(String[] args) {
		unitTest();
	}// Of main

测试中, 我简单构建了一个逻辑BP层, 这个逻辑BP层的Input部分由2个输入构成, output由3的输出构成. 使用激活函数为Sigmoid.

3.总体组合

3.1 基本参数与构造函数

public class FullAnn extends GeneralAnn {

	/**
	 * The layers.
	 */
	AnnLayer[] layers;

	/**
	 ********************
	 * The first constructor.
	 * 
	 * @param paraFilename
	 *            The arff filename.
	 * @param paraLayerNumNodes
	 *            The number of nodes for each layer (may be different).
	 * @param paraLearningRate
	 *            Learning rate.
	 * @param paraMobp
	 *            Momentum coefficient.
	 * @param paraActivators The storing the activators of each layer.
	 ********************
	 */
	public FullAnn(String paraFilename, int[] paraLayerNumNodes, double paraLearningRate,
			double paraMobp, String paraActivators) {
		super(paraFilename, paraLayerNumNodes, paraLearningRate, paraMobp);

		// Initialize layers.
		layers = new AnnLayer[numLayers - 1];
		for (int i = 0; i < layers.length; i++) {
			layers[i] = new AnnLayer(layerNumNodes[i], layerNumNodes[i + 1], paraActivators.charAt(i), paraLearningRate,
					paraMobp);
		} // Of for i
	}// Of the first constructor


    // ...

}// Of class FullAnn

FullAnn类继承了我们在BP神经网络的第一篇中编写的抽象类, 沿用了例如神经网络层数, 逐层深度, 梯度下降步长, 惯性指数mobp, 随机种子等基本成员变量.

构造函数中, 为layers数组分配空间, 同时提供了字符串paraActivitors, 字符串的长度与layers[ ]长度对应, 逐字符分别表示对应层使用激活函数.

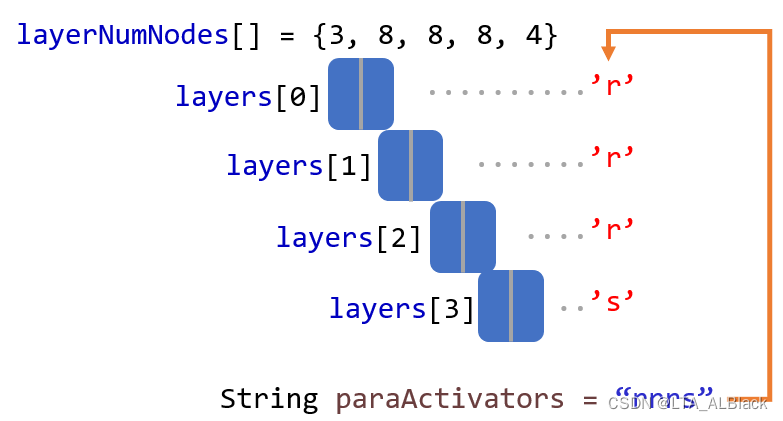
同时可以发现基本的特征, 我们肉眼所见的" 层数 " numLayers要比逻辑BP层多一个.

3.2 forward组合与backPropagation组合

	/**
	 ********************
	 * Forward prediction. This is just a stub and should be overwritten in the subclass.
	 * 
	 * @param paraInput
	 *            The input data of one instance.
	 * @return The data at the output end.
	 ********************
	 */
	public double[] forward(double[] paraInput) {
		double[] resultArray = paraInput;
		for(int i = 0; i < numLayers - 1; i ++) {
			resultArray = layers[i].forward(resultArray);
		}//Of for i
		
		return resultArray;
	}// Of forward

从第一个逻辑BP层的输入端口开始, 逐层进行forward并且得到输出数组. 同时输出数组在下一层forward中作为输入端口. 直到循环结束, 得到最终forward预测数组.(这里的forward本质上是对于抽象ANN类中虚拟接口的重写)

	/**
	 ********************
	 * Back propagation. This is just a stub and should be overwritten in the subclass.
	 * 
	 * @param paraTarget
	 *            For 3-class data, it is [0, 0, 1], [0, 1, 0] or [1, 0, 0].
	 *            
	 ********************
	 */
	public void backPropagation(double[] paraTarget) {
		double[] tempErrors = layers[numLayers - 2].getLastLayerErrors(paraTarget);
		for (int i = numLayers - 2; i >= 0; i--) {
			tempErrors = layers[i].backPropagation(tempErrors);
		}//Of for i
		
		return;
	}// Of backPropagation

先输入标签目标值, 通过getLastLayerErrors函数得到第一个惩罚处理信息, 然后带入到最后一个逻辑BP层(最后一个逻辑BP层下标数值等于numLayers - 2). 之后进行类似于forward的逐步逆向输出前导的惩罚处理信息, 逐步向前, 直到所有逻辑BP层都进行过一轮backPropagation.(这里的backPropagation本质上是对于抽象ANN类中虚拟接口的重写)

3.3 代码重现

因为forward与backPropagation都是按照ANN类中虚拟接口重写的, 因此不必再重复完成训练和测试代码了. 关于ANN抽象类代码详见我的BP神经网络第一个博客中的第2小节, 接下来重现当时博客中的最终代码:

	/**
	 ********************
	 * Test the algorithm.
	 ********************
	 */
	public static void main(String[] args) {
		int[] tempLayerNodes = { 4, 8, 8, 3 };
		FullAnn tempNetwork = new FullAnn("D:/Java DataSet/iris.arff", tempLayerNodes, 0.01,
				0.6, "sss");

		for (int round = 0; round < 5000; round++) {
			tempNetwork.train();
		} // Of for n

		double tempAccuray = tempNetwork.test();
		System.out.println("The accuracy is: " + tempAccuray);
		System.out.println("FullAnn ends.");
	}// Of main

多么相似的结果啊~ 封装应该是成功的.

4.数据测试与一些疑问(待解决)

数据测试中, 按照默认的设置: 梯度步长为0.01, 惯性因子为0.6, 训练次数改为6000次, 默认的层数安排保持{4,8,8,3}的构造, 然后分别执行了基于训练集的测试与基于70%的训练后用30%数据测试.

因为初始边权使用的是随机值, 通过我的第一篇关于BP的博客得知, 随机的初始值对于较小数据集是存在输出不稳定的情况. 因此为了避免结果的随机性, 具体在集成测试时每个样例都执行了100次并取其平均数.

最终, 通过反复测试, 得到了不同激活函数下的iris数据集最终识别率结果:

总的来说, 有些意外, 我本以为ReLU类的数据效果会更好一些, 但是效果最好的往往是例如Sigmoid这类的非线性函数, 其中以Softsign与arctan为最佳(结果要略优于Sigmoid), TanH为最次. 然后线性函数ReLU家族包括Softplus这种类线性的函数, 效果都比较糟糕.

这似乎很奇怪, 因为通过资料证明, ReLU的效果本该是不错的.

我先是通过扩大网络的深度再测试, 但是这类函数的分割数据集测试识别率总是稳定在0.29左右, 训练集测试则是不变的0.33, 也就是1/3的成功率, 换言之, 只识别了某个标签 !?

其实可以发现另一个共性, 所有识别率低的激活函数都是无界函数. 因此我猜想可能是在计算损失函数和设置惩罚时出了问题. 本文的惩罚机制是基于Sigmoid设置的, 因此输出值域是有确定的区间(0,1), 所以目标标签数组可以仅仅包含一个"1"与若干"0"构成的数据结构, 并且使用均值\(E_{k}=\frac{1}{2} \sum_{j=1}^{l}\left(\hat{y}_{j}^{k}-y_{j}^{k}\right)\)来作为损失函数. 这样的话, 每次得到的预测值都能得到一个相对公平的惩罚. 例如下面这样的预测值:

若paraTarget[i]={1,0,0}, 那么第一个数据非常接近正确目标1, 那么它只会获得0.023作用的正向激励, 而后续两个会得到-0.99758与-0.94029的逆向惩罚. 最终通过反复训练, 可以得到下面结果:

这已经非常逼近{1,0,0}(注意最后一个数据有个E-4)

但是对于ReLU还是采用这种损失函数极值就显然有问题...ReLU无上界, 随着层数的增加其会无限制增加, 其值会远大于1或者0, 就会出现下面的尴尬情况:

以上通过求差值得到的惩罚处理信息都是极大的负值:

然后边权的惩罚都非常严重.

于是后续任何数据再经过这个网络, 只有最初输入部分有实际的值, 可是但凡经过一层数据网络, 到output[ ]中立马变为负数. 这个负数还是一个绝对值比较大的负数, 以至于所有的ReLU改进版本的激活函数都无法驾驭. 最终我们神经网络输出的三个预测值都是一样的值, 要么都是0(ReLU), 要么都是-\(\alpha\). 而Leakly ReLU也许在最开始有几个数据输出不是一样的, 但是随着权的疯狂增加叠加, 最终预测值都会变成"-Infinity"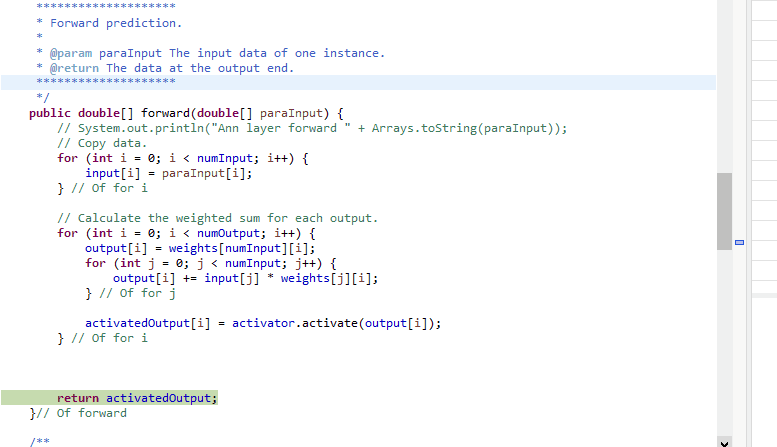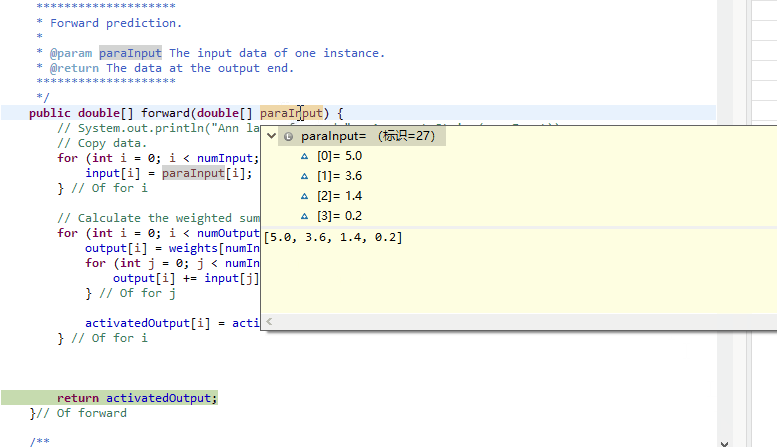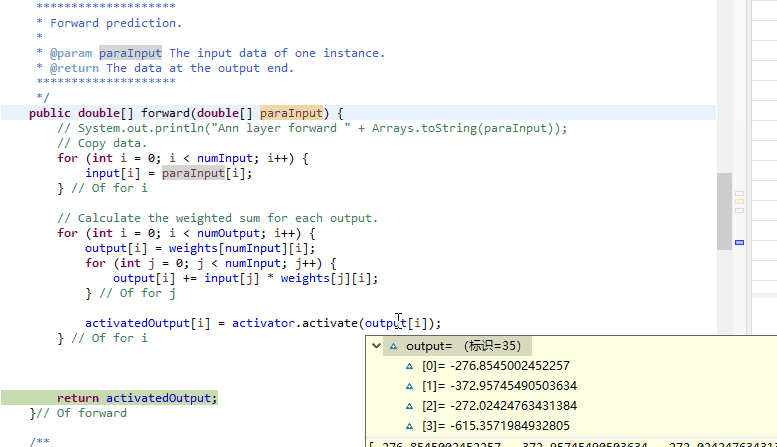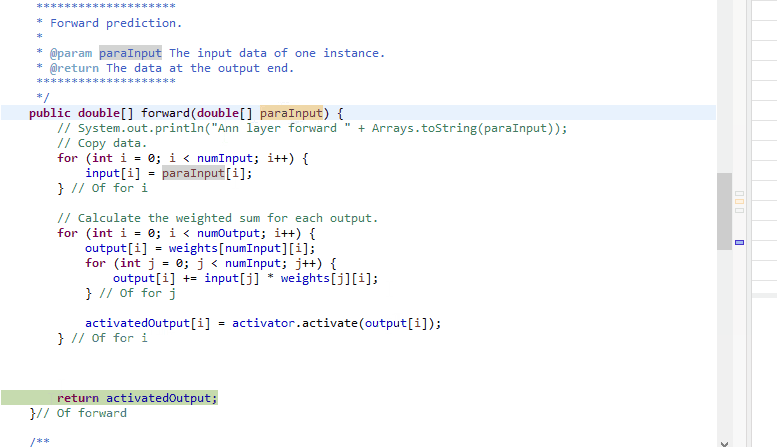

这就解释了为什么我们最终的识别率是0.33, 因为编写的argmax肯定会返回一个值, 某人第一个是最大的, 所以所有数据都预测为标签0, 自然对于iris数据集识别率就是0.33.

上面所有问题的起因都是第一次预测的值过大与不正确的目标标签值{1,0,0}导致的错误惩罚导致的. 那么是否可以在最后一层使用Sigmoid激活函数来矫正预测呢? 通过debug我发现----还是不行. 因为第一个数据第一次运行神经网络时, 在抵达最后一层之前都是执行的ReLU激活函数, 所以最后执行Sigmoid是自变量都非常大, 因此第一次预测的值就是\(\mathbf{\hat{y}}\) = {1,1,1}, 这个预测值在backPropagation计算惩罚信息时, 在执行最后一层的Sigmoid求导运算(\(y(y-1)\))时得到全0结果(惩罚信息全0), 因此这个结构无法更新网络, 无法学习.

因此要彻底解决这个问题必须针对ReLU这种无界函数设置专门的损失函数与惩罚方案, 而我们基于Sigmoid这种右半轴非线性的激活函数设计的均值损失函数的方案并不适用这种扩展激活函数.我通过一些查询得到一些策略诸如: