np.cov np.var

最新推荐文章于 2023-02-06 11:14:18 发布

原创最新推荐文章于 2023-02-06 11:14:18 发布 · 1.8k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#np.cov

numpy 专栏收录该内容

5 篇文章

订阅专栏

博客介绍了numpy中协方差和相关系数的计算方法。numpy.cov可计算协方差阵，根据bias值决定除数；np.correlate计算相关系数阵。还总结了单变量、两个及n个随机变量的计算情况，指出样本方差和协方差除以m - 1的原理相同，同时提及方差和标准差的计算函数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

协方差具体实列算法
numpy.cov(m, y=None, rowvar=1, bias=0, ddof=None)
bias=0 若样本是m,最后除以m-1
bias=1 若样本是m,最后除以m
输出是协方差阵，results[i][j]表示第i个随机变量与第j个随机变量的协方差

x = [1,3]  #x,y,z代表随机变量
y = [2,1]
z = [3,1]
m = array([[1, 3],
           [2, 1]
           [3, 1]])
 >>np.cov(m)                         # cov中每一行代表一个随机变量，每列代表一个样本
 array([[ 2. , -1. , -2. ],
       [-1. ,  0.5,  1. ],
       [-2. ,  1. ,  2. ]])

np.correlate(a, v, mode=’valid’, old_behavior=False)
计算随机变量的相关系数，以无偏估计算出来的，即以cov中bias=0 算出来的
输出结果是一个相关系数阵, results[i][j]表示第i个随机变量与第j个随机变量的相关系数.

x = [1,3]  #x,y代表随机变量
y = [2,1]
>>np.cov(x,y)
array([[ 2. , -1. ],
       [-1. ,  0.5]])
>>np.corrcoef(x,y)
array([[ 1., -1.],
       [-1.,  1.]])
X = np.vstack((x,y))
>>X
array([[1, 3],
       [2, 1]])
>>np.corrcoef(X)  
    array([[ 1., -1.],
       [-1.,  1.]])

>>> x = [-2.1, -1,  4.3]
>>> y = [3,  1.1,  0.12]
>>> X = np.vstack((x,y))
array([[-2.1 , -1.  ,  4.3 ],
       [ 3.  ,  1.1 ,  0.12]])
>>np.cov(X)
[[ 11.71        -4.286     ]
 [ -4.286        2.14413333]]
>>np.cov(x, y)
[[ 11.71        -4.286     ]
 [ -4.286        2.14413333]]
>>np.cov(x)
11.71

总结：
1 单变量 cov(x)和corrcoef(x)，x以行向量存放
2 两个随机变量 cov(x,y)和corrcoef(x，y)，x,y以行向量存放
3 n个随机变量要以行向量放在矩阵N(列表，数组等）cov(N)和corrcoef(N)
样本方差里面要除以（n-1）而不是n
协方差除以m-1原理和方差一样，因为方差为协方差的特殊情况
协方差相关系数

方差：np.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=)

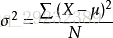
>>> a = np.array([[1, 2], [3, 4]]) #均值：(1+2+3+4)/4=0.25
>>> np.var(a)                      #（[1-0.25）^2+....+(4-0.25)^2]/4=1.25
1.25
>>> np.var(a, axis=0)              
array([ 1.,  1.])
>>> np.var(a, axis=1)
array([ 0.25,  0.25])

标准差：np.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=)

>>> a = np.array([[1, 2], [3, 4]]) #在numpy中np.std相当于对np.var开根号
>>> np.std(a)                      
 1.118033988749895
>>> np.std(a, axis=0)              
array([ 1.,  1.])
>>> np.var(a, axis=1)
array([0.5, 0.5])