一文带你读懂排序算法（四）：归并算法

最新推荐文章于 2024-03-20 10:16:40 发布

原创最新推荐文章于 2024-03-20 10:16:40 发布 · 372 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #排序算法 #数据结构 #快速排序 #分治算法

《计算机算法》专栏收录该内容

5 篇文章

订阅专栏

本文详细介绍了归并排序算法，包括其分治思想、主要步骤、算法图解和代码实现。归并排序是一种稳定的排序算法，时间复杂度为O(nlogn)，空间复杂度为O(n)。虽然需要额外空间，但在特定场景下是高效的排序选择。

点击上方蓝字关注我们

归并排序的基本思想核心是分治，就是把一个复杂的问题分成两个或多个相同或相似的子问题，然后把子问题分成更小的子问题，直到子问题可以简单的直接求解，最原问题的解就是子问题解的合并。

算法思想

归并排序的主要思想是分治法，排序的方法就是按照大小顺序合并两个元素，接着依次按照递归的返回顺序，不断地合并排好序的子数组，直到最后把整个数组的顺序排好。

主要过程是：

将n个元素从中间切开，分成两部分。（左边可能比右边多1个数）
将步骤1分成的两部分，再分别进行递归分解。直到所有部分的元素个数都为1
从最底层开始逐步合并两个排好序的数列

算法图解

举个例子，数组：[10,80,70,30,40]

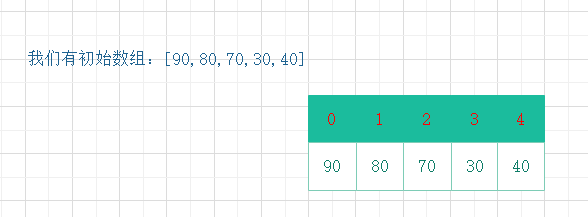
分解

分解1

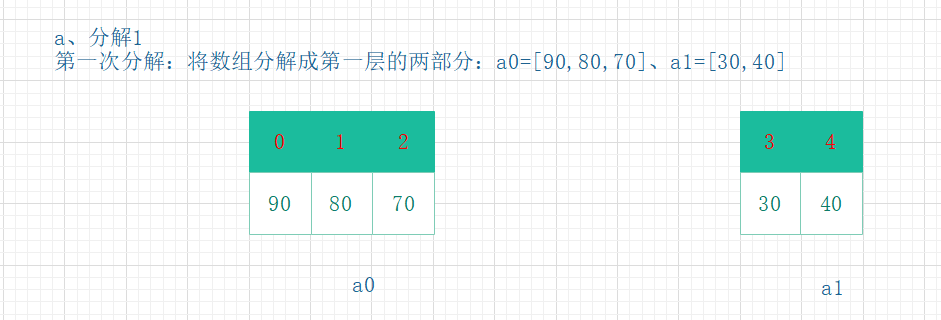
分解2

分解3

归并

归并1

归并2

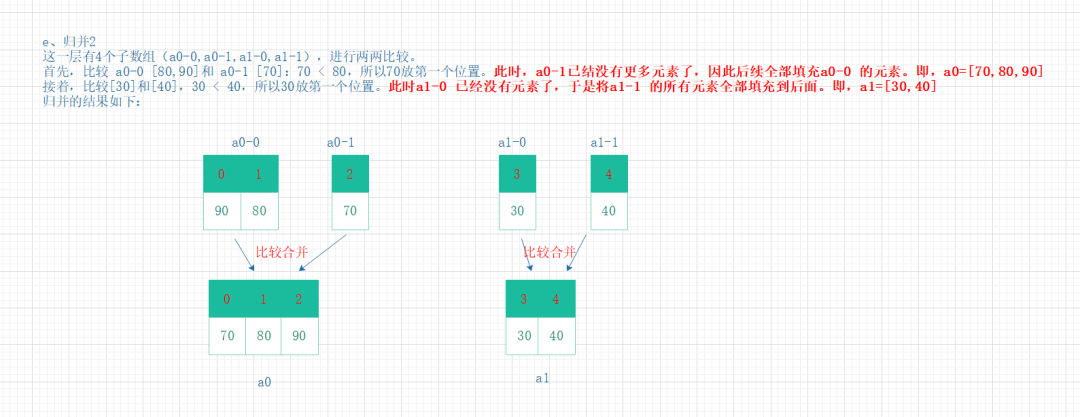
归并3

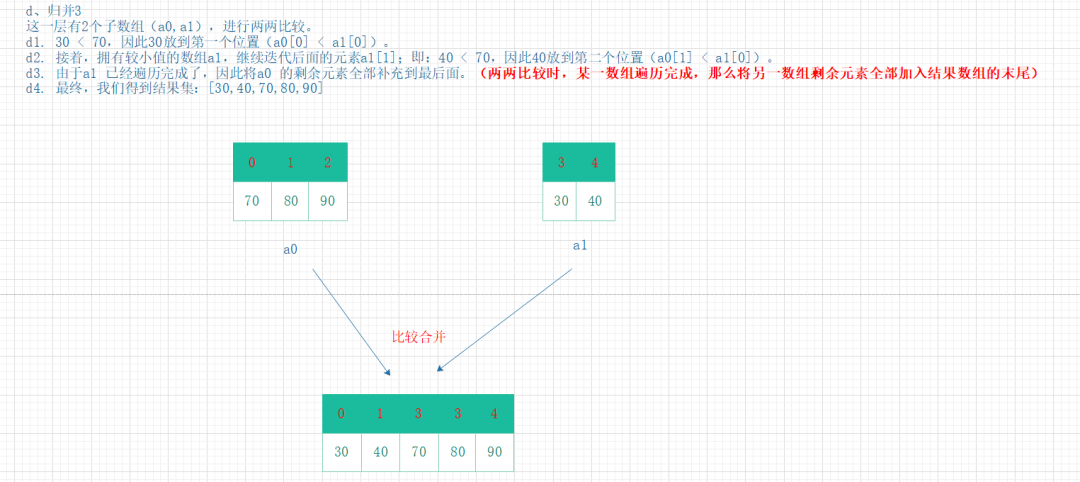
以上是归并算法操作过程的简单图示。

算法实现

代码实现：

public class MergeSort {
  public static void main(String[] args) {
    int[] arrays = {90,80,70,30,40};
    mergeSort(arrays);
    System.out.println(Arrays.toString(arrays));
  }
  public static void mergeSort(int[] array) {
    if (array == null || array.length == 0)
      return;
    int[] temp = new int[array.length];
    mergeSort(array, 0, array.length - 1, temp);
  }
  // 归并
  private static void mergeSort(int array[], int first, int last, int temp[]) {
    if (first < last) {
      int mid = (first + last) / 2;
      mergeSort(array, first, mid, temp); // 递归归并左边元素
      mergeSort(array, mid + 1, last, temp); // 递归归并右边元素
      mergeArray(array, first, mid, last, temp); // 再将二个有序数列合并
    }
  }


  /**
   * 合并两个有序数列
   * array[first]~array[mid]为第一组
   * array[mid+1]~array[last]为第二组
   * temp[]为存放两组比较结果的临时数组
   */
  private static void mergeArray(int array[], int first, int mid, int last, int temp[]) {
    int i = first, j = mid + 1; // i为第n次分解后第一组的起点, j为第n次分解后第二组的起点
    int m = mid, n = last; // m为第n次分解后第一组的终点, n为第n次分解后第二组的终点
    int k = 0; // k用于指向temp数组当前放到哪个位置
    // 比较合并：将两个有序序列循环比较, 填入数组temp
    while (i <= m && j <= n) {
      if (array[i] <= array[j]) {
        temp[k++] = array[i++];
      }
      else
        temp[k++] = array[j++];
    }
    // 如果比较完毕, 第一组还有数剩下, 则全部填入temp
    while (i <= m) { 
      temp[k++] = array[i++];
    }
    // 如果比较完毕, 第二组还有数剩下, 则全部填入temp
    while (j <= n) {
      temp[k++] = array[j++];
    }
    // 将排好序的数填回到array数组的对应位置
    for (i = 0; i < k; i++) {
      array[first + i] = temp[i];
    }
  }
}

输出结果：