图

最新推荐文章于 2024-12-06 15:58:54 发布

nyq0321

最新推荐文章于 2024-12-06 15:58:54 发布

阅读量427

点赞数

分类专栏：数据结构文章标签：数据结构

本文链接：https://blog.youkuaiyun.com/qq_27840681/article/details/106127907

版权

数据结构专栏收录该内容

12 篇文章

订阅专栏

本文详细介绍了图的定义，包括完全有向图和无向图的概念，以及连通图和强连通图的特性。重点讲解了图的表示方法如邻接矩阵和邻接表，以及图的遍历策略如深度优先搜索和广度优先搜索。接着阐述了最小生成树的Kruskal和Prim算法，以及最短路径问题的Dijkstra、Bellman-Ford和Floyd算法。最后讨论了活动网络的AOV和AOE网络，包括拓扑排序和关键路径的确定。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

图

1. 定义

（1）完全有向图：n个定点的有向图有 n(n-1)条边。
（2）完全无向图：n个定点的无向图有 n(n-1)/2条边。
（3）简单路径：路径上各顶点互相不重复。
（4）连通图和连通分量：无向图中，任意一对定点都是连通的，则该图为连通图。非连通图中的极大连通子图为连通分量。
（5）强连通图和强连通分量：有向图中，任意一对定点都是双向连通的，则该图为强连通分量。非强连通图的极大强连通子图为强连通分量。
（6）生成树：连通图的极小连通子图，n个顶点，有n-1条边。

2. 图的表示

（1）邻接矩阵
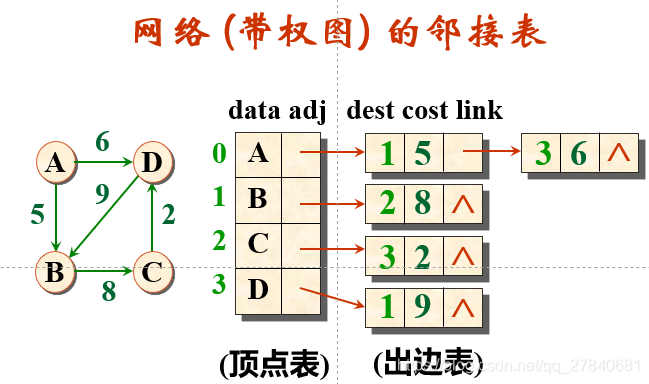
在这里插入图片描述
（2）邻接表：邻接矩阵的各行分别组织为一个单链表。

3. 图的遍历

从图的某一个顶点出发，沿着一些边访问图中的所有顶点，且每个顶点只被访问一次。
（1）深度优先搜索DFS

Node n = G.getFirstNode();
bool visited[v] = {false};
int d=0;
bool DFS(Node n, int d, bool visited[]) //从n开始搜索
{
	if(isEnd(n, d)) return true; //搜索达到某种状态d，结束
	for(Node nextNode in n)
	{
		if(!visited[nextNode])
		{
			visited[nextNode] = true;
			if(DFS(nextNode, d+1)) return true;
		}
		visited[nextNode] = false;
	}
	return false;
}

（2）广度优先搜索BFS
用队列保存当前结点

4. 最小生成树

权值最小的生成树（极小连通图，n个点，n-1条边）。

（1）Kruskal

思想：初始时，每个顶点都是一个单独的连通分量。选取权值最小的边，若该边两端的顶点不在同一个连通分量中，则将该边和顶点加入到连通图T中；否则，将该边舍去，再次选取权值最小的边，直到所有顶点再连通图中。
过程：
代码：

//利用最小堆和并查集
void Kruskal(Graph G, MinSpanTree MST)
{
	int n = G.getNumberOfV; //顶点数
	int m = G.getNumberOfE(); //边数
	MinHeap<MSTEdgeNode> H;
	UFSets F; //并查集
	
	//构建最小堆
	MSTEdgeNode ed;
	for(int i=0; i<n;i++)
	{
		for(int j=i+1;j<n;j++)
		{
			if(G.getWeight(u,v) != -1)
			{
				ed.head = u; ed.tail = v;
				ed.cost = G.getWeight(u,v);
				H.insert(ed);
			}
		}
	}

   for(int i=0;i<n;)
   {
   	if(H.empty()) return;
   	H.remove(ed);
   	int u = ed.head, v = ed.tail;
   	if(u!=v)
   	{
   		F.union(u,v);
   		MST.insert(ed);
   		i++;
   	}
   }
}

（2）Prim

思想：从某一顶点出发，选择最小权值的边，将其顶点加入到最小生成树U中。然后每一步从U中和不在U中各选一个顶点，构成的权值最小的边加入集合U中，直到所有顶点加入U中。
过程：
代码

void Prim(Graph G, MinSpanTree MST)
{
   int n = G.getNumberOfV; //顶点数
	int m = G.getNumberOfE(); //边数
	MinHeap<MSTEdgeNode> H;
....
}

（3）总结

在这里插入图片描述

5. 最短路径

单源最短路径：给定源点v，求v到其他各个顶点的最短路径。

（1）单源最短路径（非负）——Dijkstra

思想：广度优先搜索，并采用贪心的策略。声明一个dist数组保存源点到各个顶点的最短距离，并声明一个集合T保存已经找到的最短路径的顶点。初始时，更新dist为直接相连的路径长度。然后从dist中选取最短路径的顶点，加入T。此时，需要判断新加入的顶点是否对集合中其他顶点的dist有影响，（即通过该顶点到达其他点的路径是否比dist短），若有则更新dist。直到T包含所有所有顶点。
过程：

（2）单源最短路径（任意值）——Bellman-Ford

思想：从源点逐次绕过其他顶点，以缩短到达其他顶点的最短路径的方法。（图中不能包含有由负权值边组成的回路）。构建最短路径长度数组，dist1[u], dist2[u], dist3[u]…dist(n-1)[u]表示从源点到终点u经过n-1条边的最短路径长度。

（3）所有顶点之间最短路径——Floyd

思想：初始化矩阵a, a[i][j] 表示i到j的最短路径。初始化矩阵b，b[i][j]表示i到j经过b[i][j]顶点可以达到最短路径。然后进行n次更新，对每一对i和j，判断经过第0/1/2…n个结点时，最短路径是否缩小，并更新。

6. 活动网络

（1）AOV网络

定义：有向图表示一个工程，顶点表示活动，有向边<i,j>表示活动i必须先于j进行。此外，不能存在有向环。
有向环的检测：对AOV网络构造拓扑有序序列，使得网络中所有前驱和后继关系都能得到满足。如果AOV网络中有顶点不能加入拓扑序列中，则存在有向环。

（1.1）拓扑排序

定义：构造AOV网络全部顶点的拓扑有序序列的运算。
思想：选取没有直接前驱的结点，输出，然后删去该顶点和其发出的有向边。重复上面的操作，直到所有顶点均输出。如果还有未输出的顶点，说明存在有向环。
举例
代码

//对邻接表新增一个数组count，记录各顶点的入度。
//建立入度为0的顶点栈
stack<int> s;
for(int i=0;i<n;i++)
{
	if(count[i]==0) s.push(i);
}
//拓扑排序n个顶点
for(int i=0;i<n;i++)
{
	if(s.empty()) {cout<<"有回路"; return;}
	int t = s.top(); s.pop(); cout<<t<<" ";
	for(w in t的出边的顶点)
	{
		count[w]--;
		if(count[w]==0) s.push(w);
	}
}

时间复杂度：
若AOV网络中有n个顶点，e条边。每个顶点入栈一次，出栈一次。出栈时，遍历该顶点的出边，对其他顶点更新，次数为e。所以O(n+e)。

（2）AOE网络

定义：边表示工程中的活动，边上的权值表示活动的持续时间，顶点表示事件。源点：起始点，汇点：结束点。只有源点到汇点所有路径上的所有活动都完成，整个工程才算完成。
应用：完成整个工程需要多少时间？为缩短工期，应加快哪些活动？
关键路径：最长的路径，该路径决定了整个工程完成的时间，即这条路径上所有活动持续时间之和。
关键活动：关键路径上的活动（边）都为关键活动。任一关键活动延迟，整个工程延迟。任一关键活动加速，整个工程不一定提前，需要考虑关键路径上所有关键活动。
关键活动的判断：
条件：活动最早可能开始时间==活动最迟允许开始时间
（1）首先将所有事件按照拓扑排序编号。
（2）活动最早可能开始的时间：
j从活动0开始，i为前继。
（3）活动最迟允许开始时间：
j从活动n-1开始，反向递推，k为后继。