超限插值划分网格

问题描述

在计算流体力学等工程应用问题中，需要对流场等待计算区域实施网格划分，使用数值方法求得被模拟对象的数值近似解。其中，网格划分的质量（精度，光滑程度）将直接影响计算结果的质量，是复杂数值计算问题的基础。对于边界规则的简单区域，
可直接对边界参数域进行划分，将对应划分点相连即可。
在实际工程中，我们常常遇到的是一些三边或者四边的曲面单元，其边界非常复杂。因而将其映射到参数域进行网格划分时，参数域上的边界也是凹凸不平，网格质量常常难以保证，如下图所示。这就是我们希望用超限插值解决的问题。

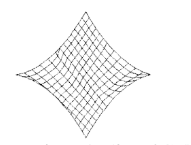
超限插值

超限插值 (transfinite interpolation) 通过对边界进行中间插值来生成网格，它与曲面片生成方法中的孔斯 (Coons) 曲面思想一样，下面以最简单的双线性混合孔斯曲面来介绍它的基本思想。
注：插值一般指给定有限个点，求经过这些点的曲线。超限插值的差值对象是曲线，也就是无限个点，这也是“超限”一词的来源。
给定由4条参数曲线构成的封闭空间曲面4边形，两对边分别定义在$u\in [0,1]$与$v\in [0,1]$上，即从已知的4条边界$p(u,0),p(u,1),p(0,v),p(1,v)$出发寻求曲面$p(u,v),0⩽u,v⩽1$.

1. 在一对$v$边界之间由线性插值构成直纹面：
   $$\begin{array}{rl}q(u,v)=& (1-u)p(0,v)+up(1,v)\\ 0& ⩽u,v⩽1\end{array}$$
2. 在一对$u$边界之间由线性插值构成直纹面：
   r(u,v)=(1−v)p(u,0)+vp(u,1)0⩽u,v⩽1\begin{aligned} r(u, v)=&(1-v) p(u, 0)+v p(u, 1) \\ 0 & \leqslant u, v \leqslant 1 \end{aligned}