% 加载标定参数和投影数据 (与原始代码相同)
x0 = 40.7337; % 旋转中心x坐标 (mm)
y0 = 56.2729; % 旋转中心y坐标 (mm)
d = 0.2768; % 探测器单元间距 (mm)
theta = [29.7099, 31.0864, 31.5971, 32.6821, 33.7591, 34.7096, 35.7295, 36.7325, 37.7390, 38.7721, 39.7407, 40.7487, 41.7212, 42.7501, 43.7181, 44.8850, 45.7493, 46.7353, 47.7589, 48.7576, 49.7721, 50.8689, 51.7972, 52.8038, 53.7884, 54.8101, 55.7980, 56.8103, 57.8121, 58.8111, 59.8053, 60.7134, 61.8225, 62.8045, 63.8152, 64.8319, 65.8198, 66.8135, 67.8222, 68.8275, 69.8002, 70.8420, 71.8235, 72.8204, 73.8449, 74.8325, 75.8369, 76.8220, 77.8254, 78.8612, 79.8361, 80.8555, 81.8363, 82.8414, 83.8152, 84.8380, 85.8329, 86.8370, 87.8406, 88.7985, 89.8575, 90.8420, 91.8376, 92.8347, 93.8274, 94.8343, 95.8495, 96.8533, 97.8447, 98.8376, 99.8249, 100.8284, 101.8158, 102.7901, 103.8212, 104.8233, 105.8161, 106.8379, 107.7885, 108.8115, 109.7627, 110.8385, 111.8493, 112.8382, 113.8094, 114.8246, 115.8568, 116.8017, 117.5860, 118.8362, 119.7962, 120.7170, 121.8258, 122.7795, 123.8136, 124.7866, 125.7994, 126.7872, 127.7953, 128.8126, 129.7837, 130.7389, 131.7958, 132.7336, 133.7594, 134.7114, 135.7237, 136.6994, 137.7431, 138.6681, 139.6991, 140.7447, 141.7168, 142.7540, 143.7195, 144.6691, 145.7325, 146.6518, 147.7909, 148.6999, 149.7510, 150.7023, 151.6825, 152.6673, 153.7474, 154.6403, 155.7223, 156.5962, 157.6610, 158.7868, 159.6204, 160.6546, 161.6124, 162.6794, 163.7354, 164.7748, 165.7526, 166.6896, 167.6524, 168.6253, 169.6467, 170.6688, 171.6476, 172.6615, 173.6523, 174.6601, 175.6680, 176.6913, 177.7070, 178.7128, 179.6960, 180.7322, 181.6779, 182.7433, 183.7157, 184.7043, 185.6989, 186.7023, 187.7025, 188.6407, 189.6866, 173.2837, 170.9319, 169.2564, 167.8857, 166.5681, 167.3659, 166.1725, 164.1979, 162.9999, 159.8616, 159.7386, 157.4562, 156.6327, 153.3389, 152.4961, 150.5074, 146.8438, 207.6903, 208.6655]; % 投影角度 (度)
R_unknown = readmatrix('附件3.xlsx'); % 180×512矩阵
% 重建参数
N_tray = 256; % 托盘图像大小
dx_tray = 100 / N_tray; % 托盘像素尺寸 (mm)
max_iter = 50; % 最大迭代次数
lambda = 0.25; % 松弛因子
%% ====== 主程序 ======
% 构建系统矩阵 (预计算或加载)
A = build_system_matrix(N_tray, theta, x0, y0, d);
% 执行SART重建
I_sart = sart_reconstruction(A, R_unknown, N_tray, max_iter, lambda);
% 输出结果
writematrix(round(I_sart, 4), 'problem2_sart.xls');
% 计算10个检测点吸收率
points = [10,18;
34.5000 ,25;
43.5000 ,33;
45 ,75.5000;
48.5000 ,55.5000;
50 ,75.5000;
56 ,76.5000;
65.5000, 37;
79.5000 ,18;
98.5000 ,43.5000;]; % 检测点坐标
absorption = zeros(10,1);
for k = 1:10
x = points(k,1);
y = points(k,2);
% 坐标转换到像素索引
i = round(x / dx_tray);
j = round(y / dx_tray);
absorption(k) = I_sart(max(1,min(N_tray,j)), max(1,min(N_tray,i)));
end
disp('SART重建吸收率:');
disp(absorption);
%% ====== 1. 构建系统矩阵 ======
function A = build_system_matrix(N_tray, theta, x0, y0, d)
% 初始化系统矩阵 (稀疏存储)
num_angles = length(theta);
num_detectors = 512;
total_rays = num_angles * num_detectors;
A = spalloc(total_rays, N_tray^2, total_rays*N_tray);
dx_tray = 100 / N_tray;
% 托盘网格坐标
x_tray = ((1:N_tray) - 0.5)* dx_tray;
y_tray = ((1:N_tray) - 0.5)* dx_tray;
% 探测器位置 (mm)
det_pos = ((1:num_detectors) - (num_detectors+1)/2) * d;
% 构建投影矩阵
ray_idx = 1;
for ang_idx = 1:num_angles
angle_rad = deg2rad(theta(ang_idx));
R = [cos(angle_rad) -sin(angle_rad); sin(angle_rad) cos(angle_rad)];
for det_idx = 1:num_detectors
% 射线起点 (旋转中心)
ray_start = [x0; y0];
% 射线方向 (考虑探测器位置)
det_offset = R * [0; det_pos(det_idx)];
ray_dir = R * [1; 0] + 1e-6 * det_offset/norm(det_offset);
ray_dir = ray_dir / norm(ray_dir);
% 遍历图像网格
for i = 1:N_tray
for j = 1:N_tray
% 像素中心坐标
pixel_center = [x_tray(i); y_tray(j)];
% 计算射线与像素的交线长度
[intersect, dist] = ray_pixel_intersect(...
ray_start, ray_dir, pixel_center, dx_tray);
if intersect
% 计算像素索引 (列优先)
pixel_idx = (j-1)*N_tray + i;
A(ray_idx, pixel_idx) = dist;
end
end
end
ray_idx = ray_idx + 1;
end
end
end
%% ====== 2. SART 迭代重建 ======
function I_sart = sart_reconstruction(A, R_flat, N_tray, max_iter, lambda)
% 初始化图像
I_vec = zeros(N_tray^2, 1);
R_flat = R_flat(:); % 展开投影数据
% 预计算行列范数
row_norms = sum(A.^2, 2);
col_norms = sum(A.^2, 1)';
% 迭代重建
for iter = 1:max_iter
residual = R_flat - A * I_vec;
% 按行更新 (ART风格)
for i = 1:size(A,1)
if row_norms(i) > 0
update = lambda * residual(i) / row_norms(i);
I_vec = I_vec + update * A(i,:)';
end
end
% 非负约束
I_vec(I_vec < 0) = 0;
% 显示迭代进度
if mod(iter,10) == 0
fprintf('Iteration %d, Residual: %.4f\n', iter, norm(residual));
end
end
% 转换为图像矩阵
I_sart = reshape(I_vec, [N_tray, N_tray]);
end
%% ====== 3. 辅助函数: 射线-像素相交检测 ======
function [intersect, dist] = ray_pixel_intersect(ray_start, ray_dir, pixel_center, pixel_size)
% 像素边界
half_size = pixel_size/2;
x_min = pixel_center(1) - half_size;
x_max = pixel_center(1) + half_size;
y_min = pixel_center(2) - half_size;
y_max = pixel_center(2) + half_size;
% 计算相交参数
t_xmin = (x_min - ray_start(1)) / ray_dir(1);
t_xmax = (x_max - ray_start(1)) / ray_dir(1);
t_ymin = (y_min - ray_start(2)) / ray_dir(2);
t_ymax = (y_max - ray_start(2)) / ray_dir(2);
t_in = max(min(t_xmin, t_xmax), min(t_ymin, t_ymax));
t_out = min(max(t_xmin, t_xmax), max(t_ymin, t_ymax));
% 检查相交
intersect = (t_in < t_out) && (t_out > 0);
if (intersect) dist = (t_out - t_in) * norm(ray_dir);
else dist = 0;
end
end
修改问题出成品
最新发布
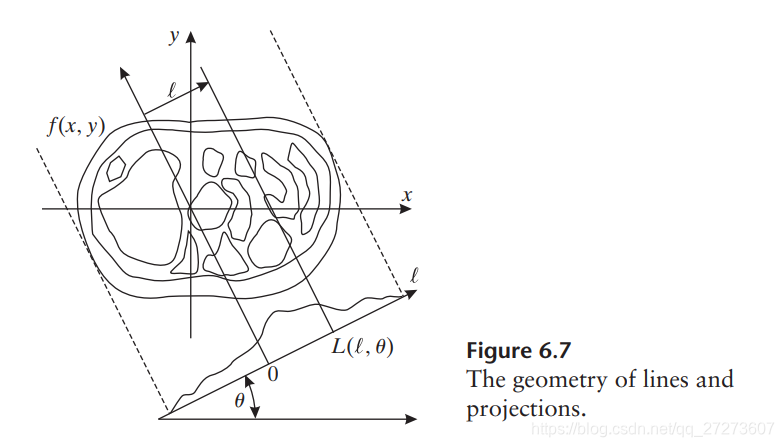
CT图像重建原理
本文探讨了CT扫描的基本测量值——线性衰减系数的线积分，并讨论了如何从这些线积分重建整个横截面的图像。重点介绍了平行射线几何下的投影理论。
扫一扫
3348
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
