【GNN】VGAE：利用变分自编码器完成图重构

今天学习的是 Thomas N. Kipf 的 2016 年的工作《Variational Graph Auto-Encoders》，目前引用量为 260 多。

VGAE 属于图自编码器，是图神经网络细分类别的一大类。Kipf 同学也非常厉害，其影响力最大的一篇论文莫过于 2017 年提出的 GCN 模型。

VGAE 全称为 Variational Graph Auto-Encoders，翻译过来就是变分图自编码器，从名字中我们也可以看出 VGAE 是应用于图上的变分自编码器，是一种无监督学习框架。

看到这可能不知道大家都没有疑问，至少我会有以下几点疑问：

1. 自编码器是利用编码与解码对数据进行压缩，加上变分后的 VGAE 是什么？
2. 自编码器是通过隐藏层节点数小于输入层节点数实现数据压缩，VGAE 如何实现？
3. 自编码器预测的目标是输入，而 VGAE 要预测的是什么？

1.Introduction

我们知道自编码器的是通过减少隐藏层神经元个数来实现重构样本，自编码器为了尽可能复现输入数据，其隐藏层必须捕捉输入数据的重要特征，从而找到能够代表原数据的主要成分。

变分图自编码器也具有类似的目的，其主要是为图中节点找寻合适的 Embedding 向量，并通过 Embedding 向量实现图重构。其中获取到的节点 Embedding 可以用于支撑下游任务。

2.VGAE

2.1 VAE

在介绍 VGAE 之前，我们先介绍下 VAE（Variational Auto-Encoders）。VAE 了解清楚后，VGAE 也算完成了 80%。

VAE 最早来源于 2014 年 Kingma 的一篇论文《Auto-Encoding Variational Bayes》。该论文目前引用数超 8300 次，作者 Kingma 和 Kipf 都来自于阿姆斯特丹大学。

VAE 是变分贝叶斯（Variational Bayesian）和神经网络的结合。

简单介绍下变分贝叶斯方法：我们知道统计模型由观察变量 x、未知参数 $\theta$ 和隐变量 z 组成，生成模型是通过隐变量来估计观察变量：$p_{\theta }(z)p_{\theta }(x|z)$。但很多情况下，这个后验概率并容易得到（因变量和参数都不知道），所以我们就需要通过其他的方式来近似估计这个后验概率。贝叶斯统计学传统的推断方法是采用马氏链蒙特卡洛（MCMC）采样方法，通过抽取大量样本给出后验分布的数值近似，但这种方法的计算代价昂贵。而变分贝叶斯是把原本的统计推断问题转换成优化问题（两个分布的距离），并利用一种分析方法来近似隐变量的后验分布，从而达到原本统计推断的问题。

而 VAE 则是利用神经网络学习来学习变分推导的参数，从而得到后验推理的似然估计。下图实线代表贝叶斯推断统计的生成模型 $p_{\theta }(z)p_{\theta }(x|z)$，虚线代表变分近似 $q_{\varphi }(z|x)$。

这篇论文里最重要的就是公式，为了简单起见，不进行公示推导。直接说结论：作者提出了 AEVB（Auto-Encoding Variational Bayesian）算法来让 $q_{\varphi }(z|x)$ 近似 $p_{\theta }(x|z)$，同时把最大似然函数的下界作为目标函数，从而避开了后验概率的计算，并且将问题转换为最优化问题，同时可以利用随机梯度下降来进行参数优化。

VAE 模型中，我们假设 $q_{\varphi }(z|x)$ 这个后验分布服从正态分布，并且对于不同样本来说都是独立的，即样本的后验分布是独立同分布的。可能大家会有个疑问：

1. 为什么是服从正态分布？
2. 为什么要强调是各样本分布是独立的？

对于第一个问题，这里只是做一个假设，只要是一个神经网络可以学到的分布即可，只是服从正态分布就是 VAE 算法，如果服从其他的分布就是其他的算法；

对于第二个问题，如果我们学到的各变量的分布都是一致的，如：

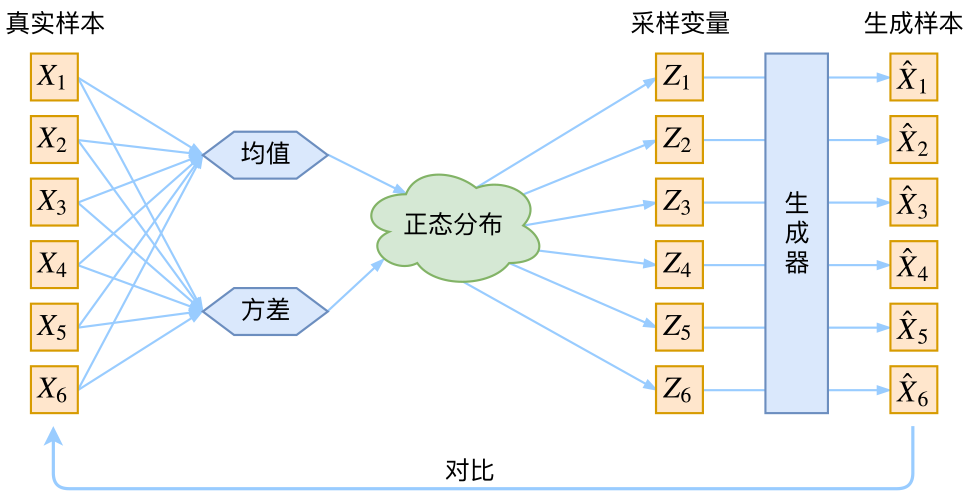
这样的结构无法保证通过学到的分布进行采样得到的隐变量 $z_i$ 能够与真实样本 $x_i$ 一一对应，所以就无法保证学习效果了。

所以 VAE 的每个样本都有自己的专属正态分布：

这样，我们便能通过每个样本的专属分布来还原出真实样本。

这也是论文中最重要的一点：
$$\log q_{\varphi }(\mathbf{z}|{\mathbf{x}}^{(i)})=\log N(\mathbf{z};{\mu }^{(i)},{\sigma }^{2(i)},\mathbf{I})$$
VAE 通过构建两个神经网络来分别学习均值和方差 μ k = f 1 ( X k ) , log ⁡ σ k 2