逻辑回归如何解决下面非线性类型的分类问题
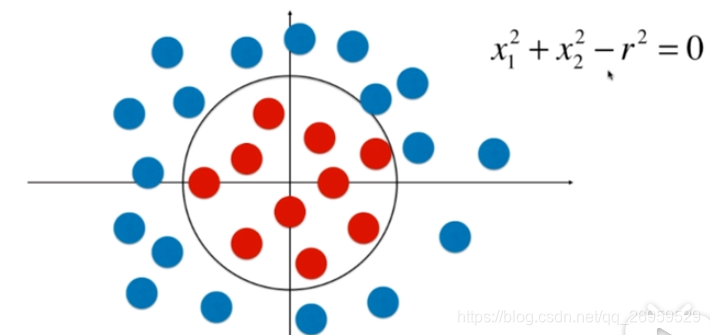
x1/x2平方项前面加上系数就是椭圆,加上x1/x2项圆心的位置就可以在坐标任意位置。加上x的立方或更高次项后,就会得到更复杂的任意边界
在实际使用多项式逻辑回归中 degree C 正则化(penalty='L1','L2') 都是超参数需要用网格搜索来确定,最适合我们数据的参数
在实际使用逻辑回归中 C 正则化(penalty='L1','L2') 都是超参数需要用网格搜索来确定,最适合我们数据的参数
1在逻辑回归中使用多项式特征(不使用sklearn)
原数据分布:
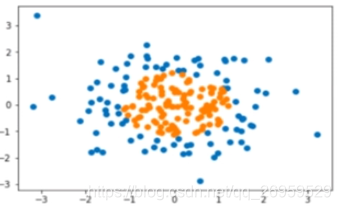
不添加多项式项时,分类结果
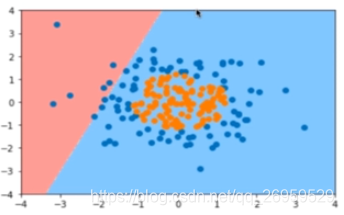
添加多项式类(使用pipleine,多项回归里也是在线性回归中加Pipeline)degree=2
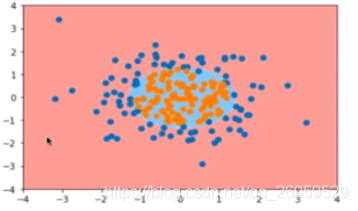
degree=20 (过拟合)
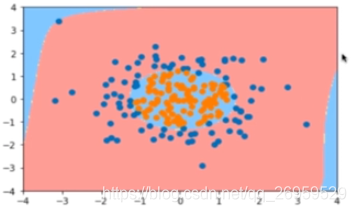
代码(自己编写)
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from playML.LogisticRegression import LogisticRegression
#定义多项式逻辑回归
def PolynomialLogisticRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression())
#此处的LogisticRegression()是自己写的,不是sklearn中的
])
poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X, y)
#绘制决策边界
plot_decision_boundary(poly_log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
2逻辑回归中使用正则化(sklearn)
2.1上节正则化表示方式
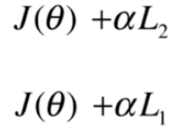
2.2新的表示正则化的方式,相当于旧方式的α变为1/α(sklearn对逻辑回归正则化,SVM中,一般采用这种)
这就意味着当使用新的方式时,不得不使用正则化,因为正则化前面的系数不可能为0,要想让正则化不重要的化只能让C非常大
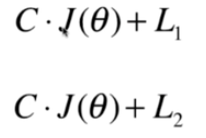
如果C越大在优化(最小化)损失函数时越会集中火力将J(θ)相应的减小到最小,但是当C非常小时,此时L1 L2正则化项就会比较重要,优化时损失函数时就会让L1L2正则化相应的小,也即限制正则化中的θ尽可能的小。
3sklearn中的逻辑回归
1.生成边界为抛物线形状的分类数据
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.normal(0, 1, size=(200, 2))
y = np.array((X[:,0]**2+X[:,1])<1.5, dtype='int')
for _ in range(20):
y[np.random.randint(200)] = 1 #随机选20个强制将类型变为1,表示添加噪音
#绘制数据
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
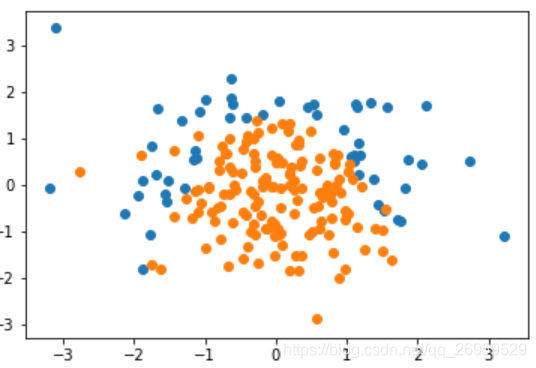
橙色在抛物线下方
2.调用sklearn中的逻辑回归
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
'''
返回结果LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)里面的系数各代表什么?
由penalty='l2':sklearn中的逻辑回归自动封装了正则化,且默认为L2正则
'''
log_reg.score(X_train, y_train) #结果:0.79
log_reg.score(X_test, y_test) #结果:0.86
3.绘制决策边界
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
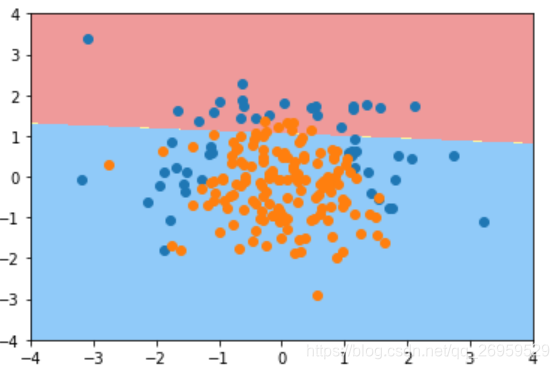
4sklearn中多项式逻辑回归
1.degree=2时
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def PolynomialLogisticRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression())
])
poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X_train, y_train)
poly_log_reg.score(X_train, y_train) #结果:0.9133
poly_log_reg.score(X_test, y_test) #结果:0.940
绘制决策边界
plot_decision_boundary(poly_log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
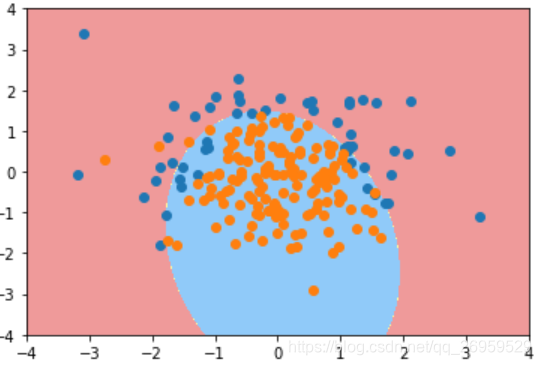
2.degree=20时 (训练集得分: 0.940测试集得分:0.920)
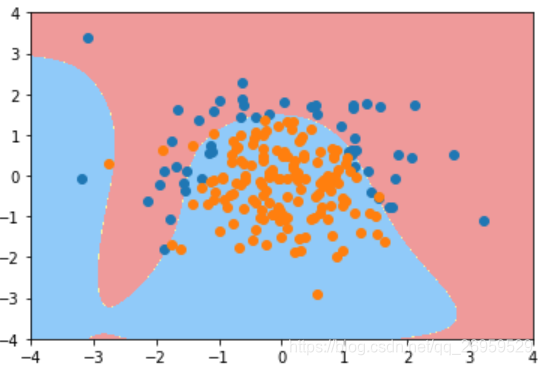
3.同时传入degree=20 和C=0.1(表示让模型正则化部分起更重要的作用,前面部分分类准确度损失函数起的作用小些)
def PolynomialLogisticRegression(degree, C):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression(C=C))
])
poly_log_reg3 = PolynomialLogisticRegression(degree=20, C=0.1)
poly_log_reg3.fit(X_train, y_train)
poly_log_reg3.score(X_train, y_train) #结果0.853
poly_log_reg3.score(X_test, y_test) #结果0.920
绘图
plot_decision_boundary(poly_log_reg3, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
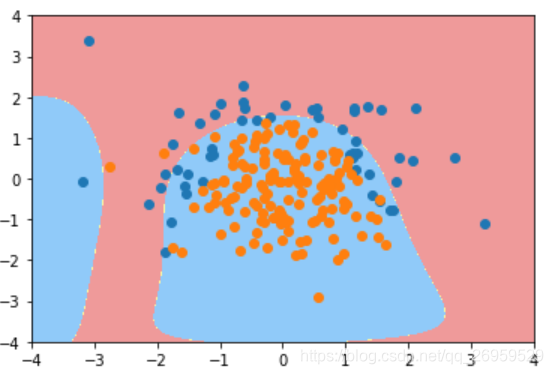
4..同时传入degree=20 和C=0.1和L1正则项
def PolynomialLogisticRegression(degree, C, penalty='l2'):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scaler', StandardScaler()),
('log_reg', LogisticRegression(C=C, penalty=penalty))
])
poly_log_reg4 = PolynomialLogisticRegression(degree=20, C=0.1, penalty='l1')
poly_log_reg4.fit(X_train, y_train)
poly_log_reg4.score(X_train, y_train) #0.827
poly_log_reg4.score(X_test, y_test) #0.900
# 由于数据比较简单加入正则得分情况不增反降在次主要看决策边界的绘制情况。
#绘制决策边界 同上
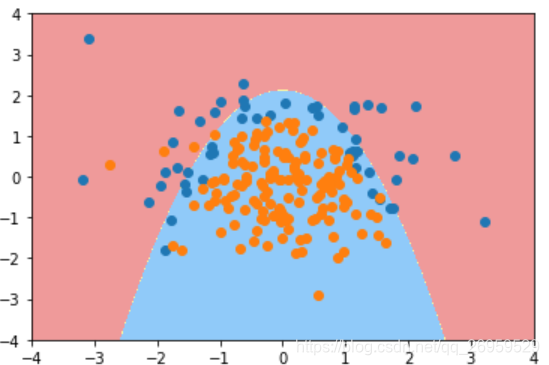
这个形状已经非常接近原始生成数据相应的形状了。再一次展示了对于使用L1这种正则项,它能够使非常多的多项式(此处为20阶)前面的系数为0。使得整个决策边界不会弯弯曲曲。不会像L2那样产生奇怪的两部分边界
在实际使用多项式逻辑回归中 degree C 正则化(penalty='L1','L2') 都是超参数需要用网格搜索来确定,最适合我们数据的参数
在实际使用逻辑回归中 C 正则化(penalty='L1','L2') 都是超参数需要用网格搜索来确定,最适合我们数据的参数
























 1016
1016

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








