DH法分为标准DH和改进DH两种，标准DH中连杆坐标系位于远端，按( heta
ightarrowd
ightarrowalpha
ightarrowa)变换，而改进DH中坐标系在近端，变换顺序为(alpha
ightarrowa
ightarrow heta
ightarrowd)。标准DH在树形或闭链机构中可能产生坐标系歧义，而改进DH能避免这种情况。
DH法是建立串联机器人连杆坐标系最常用的方法，目前学术界同时存在标准DH和改进DH两种建系方法，如图所示。连杆编号：基座为 L i n k 0 Link0 Link0，从基座往后依次定义为 L i n k 1 Link1 Link1， L i n k 2 Link2 Link2，…， L i n k i Linki Linki；关节编号： L i n k i Linki Linki离基座近的一端（近端）的关节为 J o i n t i Jointi Jointi，远的一端（远端）为关节 J o i n t i + 1 Jointi+1 Jointi+1。
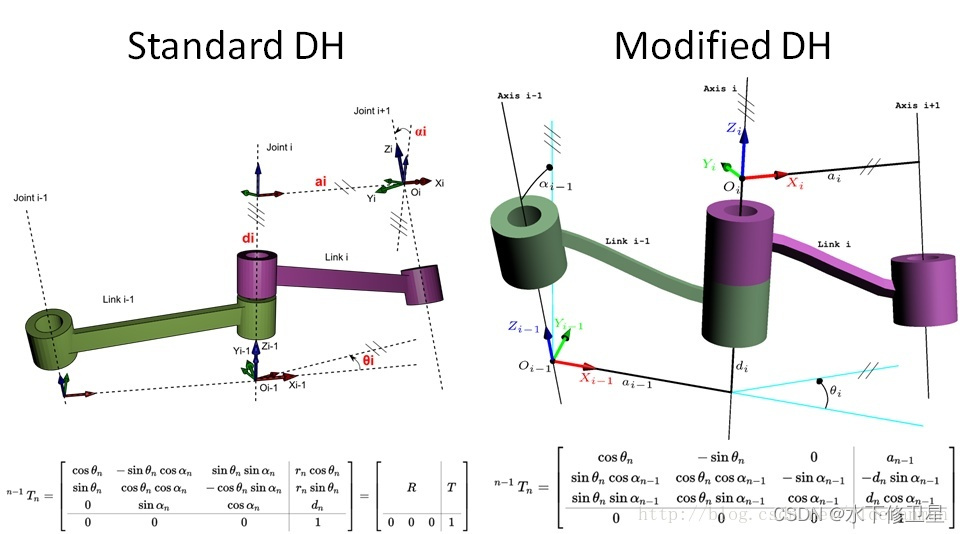
一、标准DH(Standard DH)
坐标系位置：连杆坐标系坐落于连杆远端
x
x
x轴方向：当前
z
z
z轴和前一个
z
z
z轴公垂线方向
变换顺序：
θ
→
d
→
α
→
a
\theta\rightarrow d\rightarrow\alpha\rightarrow a
θ→d→α→a
n
−
1
T
n
=
R
o
t
z
(
θ
)
T
r
a
n
s
(
d
)
R
o
t
x
(
α
)
T
r
a
n
s
(
a
)
^{n-1}T_{n}=Rotz(\theta)Trans(d)Rotx(\alpha)Trans(a)
n−1Tn=Rotz(θ)Trans(d)Rotx(α)Trans(a)
二、改进DH(Modified DH)
坐标系位置：连杆坐标系坐落于连杆近端
x
x
x轴方向：当前
z
z
z轴和后一个
z
z
z轴公垂线方向
变换顺序：
α
→
a
→
θ
→
d
\alpha\rightarrow a\rightarrow\theta\rightarrow d
α→a→θ→d
n
−
1
T
n
=
R
o
t
x
(
α
)
T
r
a
n
s
(
a
)
R
o
t
z
(
θ
)
T
r
a
n
s
(
d
)
^{n-1}T_{n}=Rotx(\alpha)Trans(a)Rotz(\theta)Trans(d)
n−1Tn=Rotx(α)Trans(a)Rotz(θ)Trans(d)
三、应用场景
对于树形结构或者闭链机构的机器人来说，按照SDH方法建立的连杆坐标系会产生歧义，因为SDH的建系原则是把连杆i的坐标系建立在连杆的远端，如图3(a)所示，这就导致连杆0上同时出现了两个坐标系。而MDH把连杆坐标系建立在每个连杆的近端，则不会坐标系重合的情况，如图3(b)所示,这就克服了SDH方法建系的缺点。
扫一扫
3193
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
