二叉搜索树

1.什么是二叉搜索树

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）, 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

2.为啥要学二叉搜索树呢？

大家都对二分查找有一定的了解吧。里面每一个元素是有序的，查找的时间复杂度是O(log(n))的。效率很高，而二叉搜索树按照中序遍历也是有序的，而且 查找、插入、删除的时间复杂度都是O(log(n))的。而二分查找插入、删除元素困难，二叉搜索树不知道比二分查找法高到哪里去了(滑稽)。

3.二叉搜索树的实现

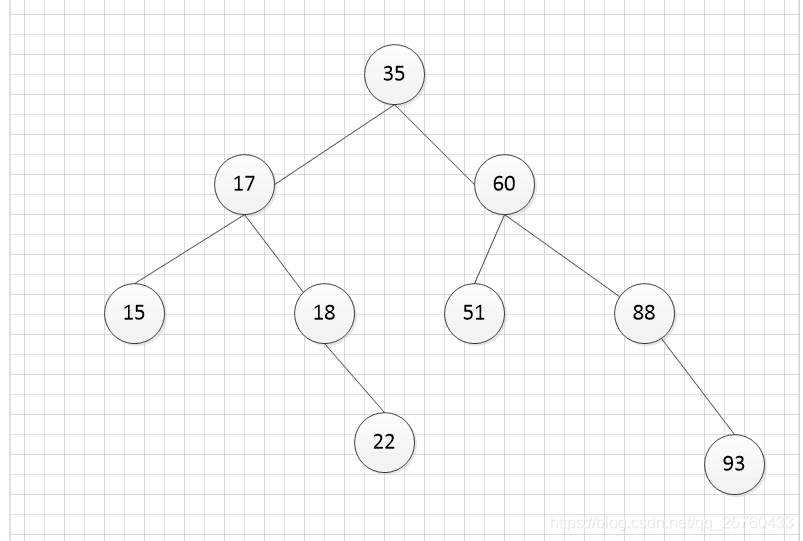
需要先根据上图创建树，下面有完整代码。

二叉搜索树的查找：

bool find_node(BTree *root,int n)   //n为要查找的值
{
	if(root==NULL)                        //不存在
		return false;
	else if(root->value==n)               //找到了
		return true;
	else if(root->value<n)                  //当前访问的节点比要查找的小，去右节点查找
		return find_node(root->rchild,n);
	else if(root->value>n)                  //当前访问的节点比要查找的大，去左节点查找
		return find_node(root->lchild,n);

}

二叉搜索树的插入：
插入节点和查找节点很相似，插入只是在为NULL的地方直接添加节点就可以了。
PS：插入一个节点时要注意二叉搜索树不允许重复关键码，插入的时候需要判断一下。

bool insert_node(BTree * &root,int n)   //n为要插入的值
{
	if(root!=NULL && root->value==n)    //如果已经存在该节点，插入失败
		return false;
	if(root==NULL)                      //在这个位置插入
	{
		root=new BTree;
		root->value = n;
		root->lchild=NULL;
		root->rchild=NULL;
		return true;
	}
	else if(root->value<n)
		return insert_node(root->rchild,n);
	else if(root->value>n)
		return insert_node(root->lchild,n);
}

二叉搜索树的删除：
（1）需要找到要删除的节点
（2）如果被删除节点的左节点为空，直接可以把其右节点挂接上去。如果被删除节点的右节点为空，把其左节点挂接上去。如果左右节点都为空，随便挂接左右节点都可以。如果左右节点都不为空，则需要在被删除节点的右子树里，找到值最小的那个节点node_min，因为node_min的值最小，所以node_min的左节点为空，直接把node_min的右节点挂接上去。然后把node_min的值赋值给被删除的节点。

贴代码

BTree * delete_min(BTree * &root)    //参数为指针的引用
{
	if(root->lchild!=NULL)                     //如果左孩子不为空，继续寻找
		return delete_min(root->lchild);
	else                                        //左孩子为空
	{
		BTree * temp=root;
		root=root->rchild;
		return temp;
	}
}

void delete_node(BTree * &root,int n)        //n为要删除的值
{
	if(root==NULL)                      //找不到节点
		cout<<"is not in tree"<<endl;
	else if(root->value>n)
		delete_node(root->lchild,n);
	else if(root->value<n)
		delete_node(root->rchild,n);
	else                                  //找到该节点，进行删除操作
	{    
		BTree * temp = root;
		if(root->lchild==NULL)            //左孩子为空，挂接右孩子
			root=root->rchild;
		else if(root->rchild==NULL)        //右孩子为空，挂接左孩子
			root=root->lchild;
		else                              //都不为空
		{
			temp=delete_min(root->rchild);
			root->value=temp->value;
			
		}
		delete temp;
	}
}

下面贴个完整代码

#include<iostream>
using namespace std;

struct BTree
{
	int value;
	BTree *lchild;
	BTree *rchild;
};

BTree * Created(int *num,int &index)          //根据数组创建二叉树
{
	if(num[index]==0)
		return NULL;
	else
	{
		BTree *root=new BTree;
		root->value=num[index];
		root->lchild=Created(num,++index);
		root->rchild=Created(num,++index);
		return root;
	}
}
bool find_node(BTree *root,int n)     //n为要查找的值
{
	if(root==NULL)                        //不存在
		return false;
	else if(root->value==n)               //找到了
		return true;
	else if(root->value<n)                  //当前访问的节点比要查找的小，去右节点查找
		return find_node(root->rchild,n);
	else if(root->value>n)                  //当前访问的节点比要查找的大，去左节点查找
		return find_node(root->lchild,n);

}
bool insert_node(BTree * &root,int n)    //n为要插入的值
{
	if(root!=NULL && root->value==n)    //如果已经存在该节点，插入失败
		return false;
	if(root==NULL)                      //在这个位置插入
	{
		root=new BTree;
		root->value = n;
		root->lchild=NULL;
		root->rchild=NULL;
		return true;
	}
	else if(root->value<n)
		return insert_node(root->rchild,n);
	else if(root->value>n)
		return insert_node(root->lchild,n);
}
void in_print(BTree *root)               //中序遍历
{
	if(root==NULL)
		return ;
	in_print(root->lchild);
	cout<<root->value<<" ";
	in_print(root->rchild);
}
BTree * delete_min(BTree * &root)    //指针的引用
{
	if(root->lchild!=NULL)                     //如果左孩子不为空，继续寻找
		return delete_min(root->lchild);
	else                                        //左孩子为空
	{
		BTree * temp=root;
		root=root->rchild;
		return temp;
	}
}

void delete_node(BTree * &root,int n)    //n为要删除的值
{
	if(root==NULL)                      //找不到节点
		cout<<"is not in tree"<<endl;
	else if(root->value>n)
		delete_node(root->lchild,n);
	else if(root->value<n)
		delete_node(root->rchild,n);
	else                                  //找到该节点，进行删除操作
	{    
		BTree * temp = root;
		if(root->lchild==NULL)            //左孩子为空，挂接右孩子
			root=root->rchild;
		else if(root->rchild==NULL)        //右孩子为空，挂接左孩子
			root=root->lchild;
		else                              //都不为空
		{
			temp=delete_min(root->rchild);
			root->value=temp->value;
			
		}
		delete temp;
	}
}
void print(BTree *root,int h)           //树形打印
{
	if(root!=NULL)
	{
		print(root->rchild,h+1);
		for(int i=0;i<h;i++)
			cout<<"     ";
		cout<<root->value;
		print(root->lchild,h+1);
	}
	cout<<endl;
}
int main()
{
	int h;
	int num[]={35,17,15,0,0,18,0,22,0,0,60,51,0,0,88,0,93,0,0};
	BTree *root=NULL;
	int index=0;
	root=Created(num,index); 	
	cout<<"初始二叉树"<<endl;
	print(root,0);             
	
	cout<<"输入要查找的数字"<<endl;
	int find_num;
	cin>>find_num;
	if( find_node(root,find_num))
		cout<<"查找成功"<<endl;
	else 
		cout<<"查找失败"<<endl;

	cout<<"请输入要插入的数字"<<endl;
	int insert_num;
	cin>>insert_num;
	if( insert_node(root,insert_num))
		cout<<"插入成功"<<endl;
	else
		cout<<"已经存在该节点"<<endl;
	print(root,0);

	cout<<"请输入要删除的数字"<<endl;
	int delete_num;
	cin>>delete_num;
	delete_node(root,delete_num);
	print(root,0);
	return 0;
}

运行结果：
测试查找

测试插入

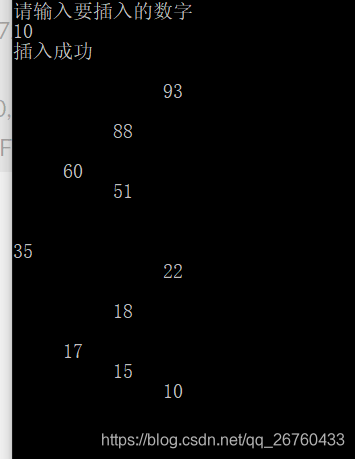
删除测试

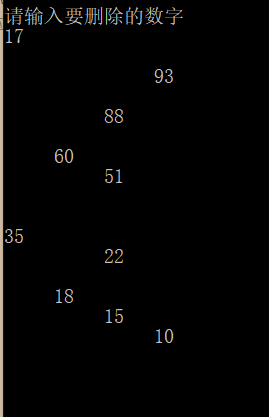
PS：本人小白，如有错误欢迎指出 q(≧▽≦q)。