[数据结构与编程]-链表

链表(List)在计算机编程中，是一种常见且十分重要的数据结构。相比数组等连续式内存布局，链表在内存空间中的布局是离散的，通过指针来进行索引，因此具有更强的灵活性。在对程序员能力的考查中，链表也是数据结构方面的重点内容之一，这种数据结构相对简单，具有很好的逻辑性，只需要掌握其本质，那么，基本上大多涉及链表的Problem都能够迎刃而解。

 

一、链表的空间布局

若要细分，链表的种类大致可以分为单链表、双向链表、循环链表等，单本质上性质都是大同小异。这里以典型的单链表为例，其具有以下的空间布局:

、

可以看到，每个节点除了自身所维护的内容(contents)外，还有一个指向其他节点的指针next，通过指针，可以遍历整个链表中的任一节点。

链表的这种空间布局相比连续式内存布局(比如C-array、STL vector、STL deque等)具有的最大优势是:灵活

所谓的“灵活”可以这么理解:进行更易(比如插入、删除)型操作时，链表的时间消耗更小，几乎是常数级别。因为无论是插入还是删除操作，只需要通过改变节点的next指针指向即可完成，以下示例删除操作：

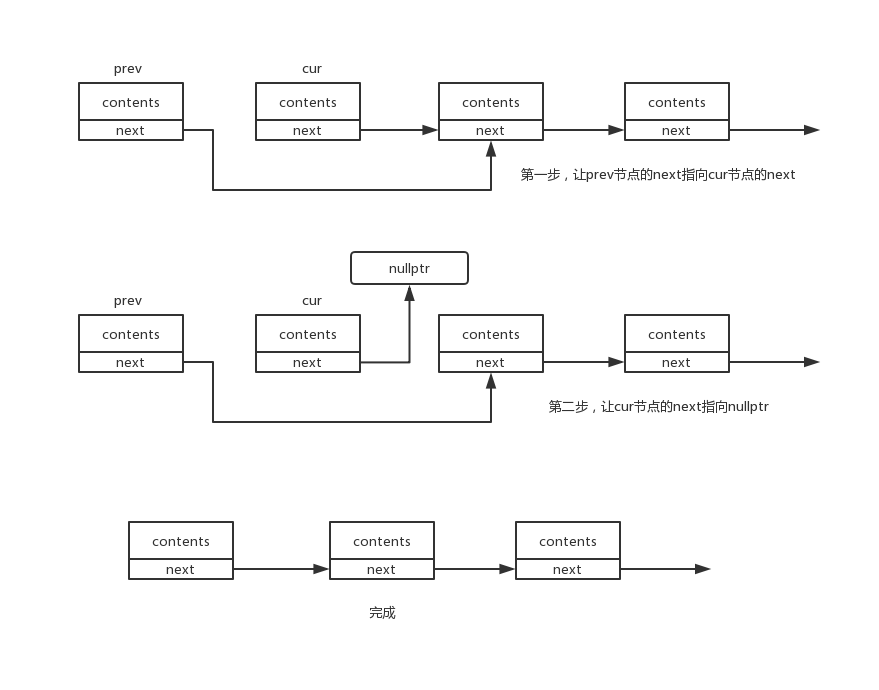
可以看到，在删除的过程中，仅仅伴随当前节点和当前节点的前一节点的指针操作，任何节点的空间布局都没有产生变化，删除操作的时间复杂度为O(1)。

 

再如插入操作：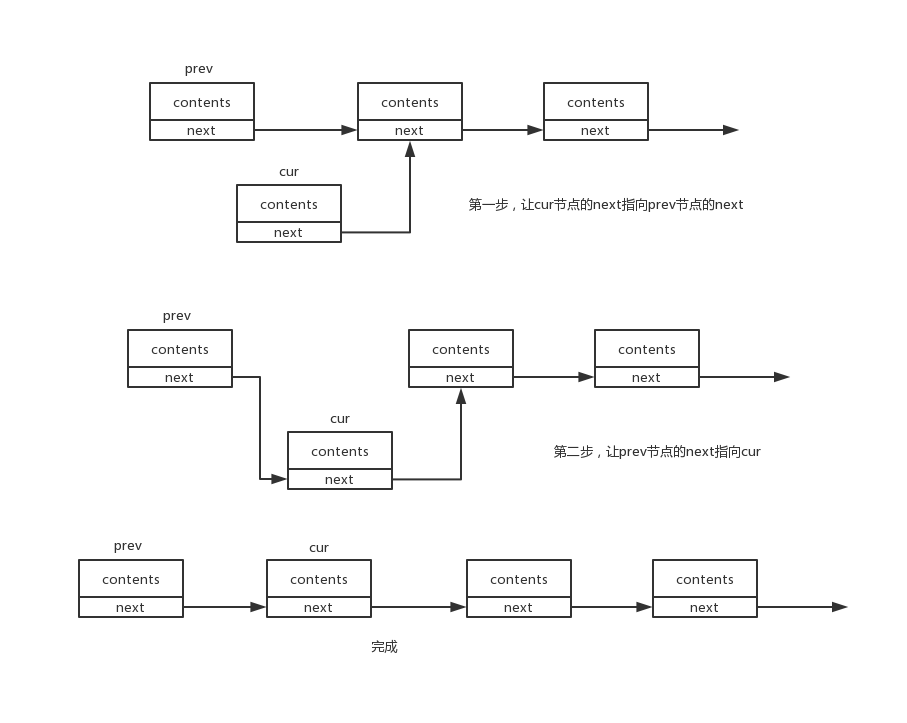

可见，插入操作也仅仅涉及部分节点的指针操作，时间复杂度为O(1)。

但，对于连续式内存布局来说，更易型操作往往将会涉及到内存的重新分配---比如对于一个STL vector容器，尽管其会自动地分配内存空间(当内存空间不够时，会自动翻倍)，但对于已经分配好的部分来说，比如当前数组内容为{1,2,3,4,6,7,8,9}，假如我们要将一个int类型的变量(int x = 5)插入到数组中合适的位置，也就是4之后，可以看看，进行插入操作会带来怎样的结果：

首先，在4以及其之前的布局不会产生变化:1、2、3、4所对应的内存地址不变。

为了插入5，并且满足连续式的内存布局，也就意味着需要将原本‘6’所处的位置替换为5.而原本'7'的位置替换为'6'...以此类推，可以看到，自6之后的所有数字，在插入‘5’后，其内存地址都“向后”移动了一个int的长度。可以很直观地看出，在连续式内存布局下，进行更易型操作地平均时间复杂度是O(n)。

当然，链表的“灵活性”的代价是，无法直接寻址(直接寻址需要连续式内存分布)，直接的后果是在进行查找操作时的时间复杂度是O(n),而连续式内存分布由于可以直接寻址，所以其查找的时间复杂度是常数级。

另外值得注意的是，对连续式内存分布的容器进行更易型操作，往往会导致原本指向其中的迭代器、引用、指针失效(很显然，因为内存进行了冲分配)，而对于链表来说，这种问题便从根源上不会存在。

 

二、链表的基本操作

链表的操作往往是程序员们所真正关注的问题，要用好这种数据结构，必然需要对链表的各种操作(尤其是更易型)心知肚明。这里列举一些常见且重要的操作.

 

插入

为了进行插入操作，我们需要的“已知内容”为插入位置的前一个节点信息(ListNode* prev)。

插入操作的步骤是，先让待插入的节点的next指针指向插入位置所对应的节点，然后让prev节点的next指针指向该节点即可。通常伪代码如下：

cur->next = prev->next;

prev->next = cur;

 

删除

为了进行删除操作，同样，我们需要知道待删除节点的前一个节点信息(ListNode* prev)

删除操作的步骤是，先让待删除节点的前一节点的next指向待删除节点的下一节点，然后让待删除节点的next指向nullptr；

prev->next = cur->next;

cur->next = nullptr;

 

合并

合并操作十分简单，对于两个链表L1和L2，合并的方式就是让L1的尾节点指向L2的头节点。

tail1->next = head2;

 

翻转

链表的翻转操作相对复杂一些，但却也十分重要，这里推荐一种常用的方式:头插法。

头插法的具体步骤为:首先建立一个新的、空的链表(包括一个虚头dummy)，然后依次遍历原链表，每遍历到一个节点，就将其插入到新链表的头处(dummy->next)，伪代码如下：

while(cur){

ListNode *nextC = cur->next;

cur->next = dummy->next;

dummy->next = cur;

cur = nextC;

}

在翻转链表中，用到了一种叫做“虚头”的小技巧，这种技巧是解决链表相关problem的一大利器，随后会介绍这种技巧。

 

链表操作中的一些技巧

 

虚头

虚头是在链表操作中一种常用的技巧，其应用的目的在于，设立一个不变的节点，这样，无论我们对后序节点进行怎样的操作，最终总能方便地返回新的表头。

比如，像先前的翻转操作，如果不使用虚头的话，想一想，如果从头节点开始遍历，那么怎么插入这个节点到新链表呢？

或者，我们一开始只知道原head节点，经过一系列更易操作后，当前的head已经不是原本的head了，又该怎么返回此时的表头呢？

不妨使用虚头，这样以上类似的问题就不再是问题了。

使用虚头的方式很简单，我们只需要为其分配一个适当的空间并进行“符合逻辑的初始化”即可。

比如这样：

ListNode* dummy = new ListNode(-1);

dummy->next = head;

这样，经过一些列操作后，要得到当前的表头，只需要返回dummy->next即可，非常方便。

 

取中位

对于连续式内存分布的容器而言，我们可以很容易得到其中位索引(size/2)，因此可以很方便地取得其中位元素。那么对于链表而言，要怎样取得其中位元素呢？

假设不使用STL容器，我们无法直接取得链表的大小，这时候应该怎么做？

方法一：最直白的方式当然是遍历两遍链表，第一次用来取得链表的长度，第二次遍历时只需要在“走过链表长度一半时”取得对应节点即可。

而还有更好的方法，也就是一遍遍历的方式：设置两个指针，一快一慢，快的指针每次走两步，慢的指针每次走一步，这样当快指针已经遍历完链表时，慢指针所指的位置就是链表的中位了！伪代码如下：

while(fast && fast->next){

fast = fast->next->next;

slow = slow->next;

}

 

环形链表

如果一个链表中存在环路，我们要怎么知道有这个环路存在？

其实，方法也很简单，和取中位一样，我们设置两个指针，一快一慢，因为快的指针一定比慢的指针先到环路中，这样，如果随后慢指针会与快指针相遇(fast == slow)那不就意味着链表中存在环路吗？

进阶:怎样知道环路的入口？

让我们延续之前的思想，首先，设置一快一慢两个指针，让快指针一次走两步，慢指针一次走一步，那么它们一定会在环路的某个位置相遇。

现在，让我们假设环路的入口处距离起点的距离为x、假设相遇点距离环路入口的距离为a；

显然，在第一次相遇时，如果慢节点走过的距离为L = x + a,那么快节点走过的距离应当是2L = 2x + 2a = x + a + nr（相当于说，是快节点到达未来的相遇点后，又多走了n圈环路，r表示环路的长度）

所以可以得到 x + a = nr ------> x = (n-1)r + (r - a)

这里，r-a也就表示从相遇点往后到环入口的距离。

现在，问题也就豁然开朗了：让慢节点走x步，其一定会回到环入口！（可以看出慢节点先走了r-a步道环入口，然后又绕了n-1圈），所以在第一次相遇后，我们只需要再重新设一个慢节点，让其从头开始遍历，而原本的慢节点也继续”前进“，这样，当两个节点都走了x步，便一定会在环入口相遇。伪代码如下：

while(fast && fast->next){

fast  =fast->next->next;

slow = slow->next;

if(slow == fast){

    ListNode* slow2 = head;

    while(slow2 != slow){

     slow = slow->next;

     slow2 = slow2->next;

   }

    return slow2;

  }

}

 

合并两个有序链表(保证合并后链表有序)

此问题有很多种思路，但遇到"有序"问题时，我们往往可以借助其他数据结构.比如二项堆，二项堆可以分为大顶堆和小顶堆，其保证顶部的节点一定是最大/最小的，如果我们先遍历两个链表，并把其节点与值的对(pair)存储在二项堆中，随后，新建一个链表，并依次弹出堆顶元素并插入到新链表，问题便得以解决。

伪代码如下:

priority_queue<pair<int,ListNode*>> Q;

for(auto i : list1)

   Q.push(i);

for(auto j: list2)

  Q.push(j);

ListNode* dummy = new ListNode(-1);

ListNode* cur = dummy;

while(!Q.empty()){

   auto p = Q.top();

   Q.pop();

   p.second->next = cur->next;

   cur->next = p.second;

   cur = cur->next;

}

 

总结

有关链表问题，大多无非涉及上述所言的操作与技巧，问题是变化的，但数据结构的本质并没有变化，许多看似简单的数据结构，实际也有许多值得注意的细节，关于链表的介绍不多做赘述。