POJ-Catch That Cow BFS+队列

最新推荐文章于 2020-11-16 12:21:33 发布

熊子q

最新推荐文章于 2020-11-16 12:21:33 发布

阅读量615

点赞数 1

CC 4.0 BY-SA版权

分类专栏：刷题

本文链接：https://blog.youkuaiyun.com/qq_26235879/article/details/95220384

刷题专栏收录该内容

57 篇文章

订阅专栏

博客围绕Catch That Cow题目展开，介绍其时间、内存限制等信息。题目中农夫John要抓牛，有步行和瞬移两种移动方式。解题采用bfs+队列算法，作者参考大佬博客了解BFS大致思路，还画了BFS树状结构图，最后给出代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题链接：http://poj.org/problem?id=3278

算法：bfs+队列

Catch That Cow
Time Limit: 2000MS Memory Limit: 65536K
Total Submissions: 32679 Accepted: 10060

Description

Farmer John has been informed of the location of a fugitive cow and wants to catch her immediately. He starts at a point N (0 ≤ N ≤ 100,000) on a number line and the cow is at a point K (0 ≤ K ≤ 100,000) on the same number line. Farmer John has two modes of transportation: walking and teleporting.

Walking: FJ can move from any point X to the points X - 1 or X + 1 in a single minute
Teleporting: FJ can move from any point X to the point 2 × X in a single minute.

If the cow, unaware of its pursuit, does not move at all, how long does it take for Farmer John to retrieve it?

Input
Line 1: Two space-separated integers: N and K

Output
Line 1: The least amount of time, in minutes, it takes for Farmer John to catch the fugitive cow.

Sample Input
5 17

Sample Output
4

Hint
The fastest way for Farmer John to reach the fugitive cow is to move along the following path: 5-10-9-18-17, which takes 4 minutes.

做题过程
看了半天大佬的博客，懵懵懂懂的知道了BFS的大致思路
大佬的BFS解释

然后自己根据这道题画了个大致的图，如下图所示:
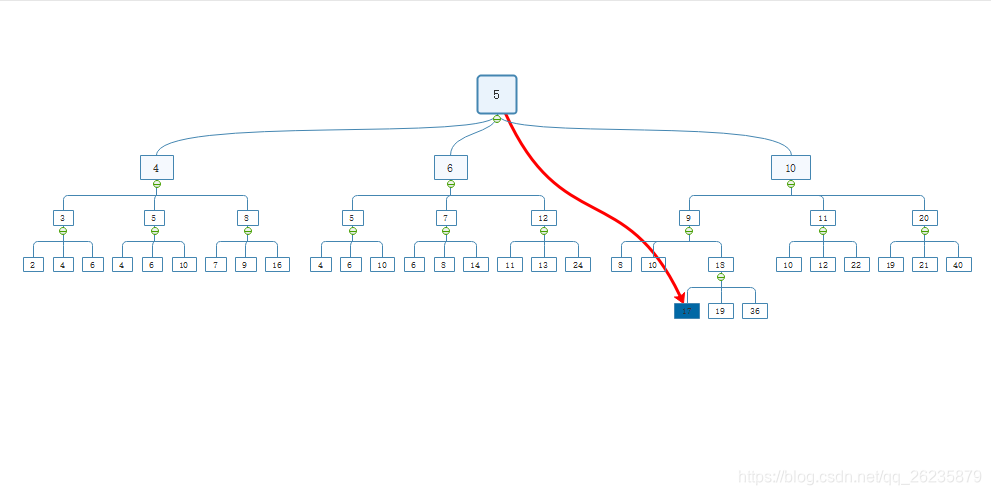
在这里插入图片描述

BFS树状结构图
大致思路
利用队列的先进先出特性，将下一层三种走法的结果入队，然后再取出队首计算三种走法，入队，以此类推，知道找到终点k位置，即为所求。

代码

//Catch That Cow
//抓住那个奶牛！！！
/**
利用BFS+Queue队列
**/
#include<iostream>
#include<queue>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=100001;//边界值
bool vis[maxn];//记录该点是否通过
int step[maxn];//记录到达该点的步数
queue<int> q;

int BFS(int n,int k)
{
    int head,next;
    q.push(n);
    step[n]=0;
    vis[n]=true;
    while(!q.empty())
    {//判断队不为空
        head=q.front();//获取队头
        q.pop();
        for(int i=0;i<3;i++)
        {//三种走路方法
            if(i==0)next=head-1;
            else if(i==1)next=head+1;
            else if(i==2)next=head*2;
            if(next<0||next>=maxn)continue;
            if(!vis[next])//如果该点没有访问过
            {
                q.push(next);
                step[next]=step[head]+1;
                vis[next]=true;
            }
            if(next==k)return step[next];
        }
    }
}
int main()
{
    int n,k;
    while(cin>>n>>k)
    {
        memset(step,0,sizeof(step));
        memset(vis,false,sizeof(vis));
        while(!q.empty()) q.pop(); //注意调用前要先清空
        if(n>=k) printf("%d\n",n-k);
        else printf("%d\n",BFS(n,k));
    }
    return 0;
}