APIO2014 Beads ans wires[树形DP]

[APIO2014] Beads and wires

---

Question：

有一个点，可以通过两种方式添加节点
$Append(w, v)$：一个新的珠子 $w$ 和一个已经添加的珠子 $v$ 用红线连接起来。

$Insert(w, u, v)$：一个新的珠子 $w$ 插入到用红线连起来的两个珠子$u, v$之间。具体过程是删去$u, v$之间红线，分别用蓝线连接 $u, w$ 和 $w, v$ 。

现在告诉你最终状态（点和连接方式，不告诉颜色）求最大可能得分

---

Solution

树形DP ？？
对于有贡献的链上的点貌似都会长成这个样子

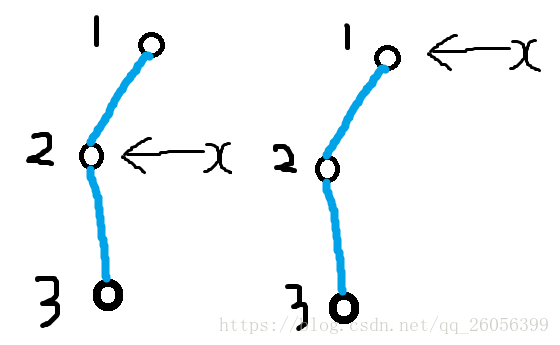
而且这些点都是有顺序的 （暂且把图中 2结点 称为 A点 1，3节点称为 B点）

因为有些情况是不会出现的（好像只有一种情况），像这样

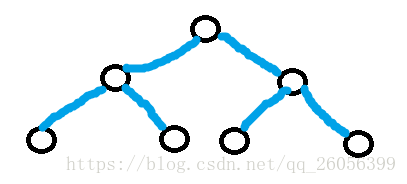
两个A点被红边或蓝边连接起来了
所以枚举状态时记录一下出现了几个A点就行

$G[i][x][y]$表示$i$点与它的子节点连了x个蓝边，且在儿子中出现了y个A点
$F[i][j]$ 是用来记录最大值，减少代码量的

然后瞎转移就好了，$O(n)$
本蒟蒻写的树形DP都是这个鬼模样，很麻烦
有点像 摧毁树状图 那个题

---

冗长代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>
#include <cmath>
#define For(i,s,e) for(int i=(s); i<=(e); i++)
#define Rep(i,s,e) for(int i=(s); i>=(e); i--)
using namespace std;

typedef long long LL;
const int N=1000000+1, M=100000+1, Inf=1000000007;

struct Node{
    int x, nxt, w;
}T[N];

int n, m;

int h[N], len;
void addEdge(int x, int y, int w){
    T[++len]=(Node){ y, h[x], w}; h[x]=len;
}

int F[N][3], g[N][3][2];

void dp(int x, int fa){

    F[x][0]=0; F[x][1]=F[x][2]=-Inf;
    for(int p=h[x]; p; p=T[p].nxt){
        int v=T[p].x; if(v==fa) continue;

        dp(v, x);
    }

    g[x][0][0]=0, g[x][1][1]=g[x][1][0]=g[x][2][0]=g[x][2][1]=-Inf;
    for(int p=h[x]; p; p=T[p].nxt){
        int v=T[p].x; if(v==fa) continue;
        g[x][2][1]=max(g[x][2][1]+max(g[v][1][0]+T[p].w, g[v][0][0]), max(g[x][1][0]+T[p].w+max(F[v][2], g[v][0][1]), g[x][1][1]+T[p].w+g[v][0][0]));
        g[x][2][0]=max(g[x][2][0]+max(g[v][1][0]+T[p].w, g[v][0][0]), g[x][1][0]+T[p].w+g[v][0][0]);

        g[x][1][1]=max(g[x][1][1]+max(g[v][1][0]+T[p].w, g[v][0][0]), g[x][0][0]+T[p].w+max(F[v][2], g[v][0][1]));
        g[x][1][0]=max(g[x][1][0]+max(g[v][1][0]+T[p].w, g[v][0][0]), g[x][0][0]+T[p].w+g[v][0][0]);

        g[x][0][1]=max(g[x][0][1]+max(g[v][1][0]+T[p].w, g[v][0][0]), g[x][0][0]+max(T[p].w+g[v][1][1], max(F[v][2], g[v][0][1])));
        g[x][0][0]=g[x][0][0]+max(g[v][1][0]+T[p].w, g[v][0][0]);
    }

    F[x][0]=max(g[x][0][0], g[x][0][1]);
    F[x][1]=max(g[x][1][0], g[x][1][1]);
    F[x][2]=max(g[x][2][0], g[x][2][1]);
}

int main(){
    ios::sync_with_stdio(false);
    cin>>n;

    For(i,1,n-1){
        int a, b, c; cin>>a>>b>>c;
        addEdge(a, b, c); addEdge(b, a, c);
    }

    dp(1,0);

    cout<<max(F[1][0], F[1][2])<<endl;

    return 0;
}