本文详细介绍了非负矩阵分解（NMF）的基本思想、原理及应用，阐述了为何选择非负矩阵及其优势，深入解析了NMF的算法实现，包括平方距离和KL散度两种损失函数的定义及迭代更新规则。
非负矩阵分解(NMF)
- NMF的基本思想
- 为什么分解的矩阵式非负？
- 为什么要运用非负矩阵分解？
- 非负矩阵分解的算法和实现
- 两种损失函数的定义方式
- 平方距离
- KL散度
- 算法步骤
- 平方距离
- KL散度
- 非负矩阵分解的伪代码
- 非负矩阵分解的实现代码
NMF的基本思想：
对于任意给定的一个非负矩阵V，NMF算法能够通过计算，从原矩阵提取权重矩阵和特征矩阵两个不同的矩阵出来。（限制条件：W和H中的所有元素都要大于0）
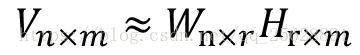
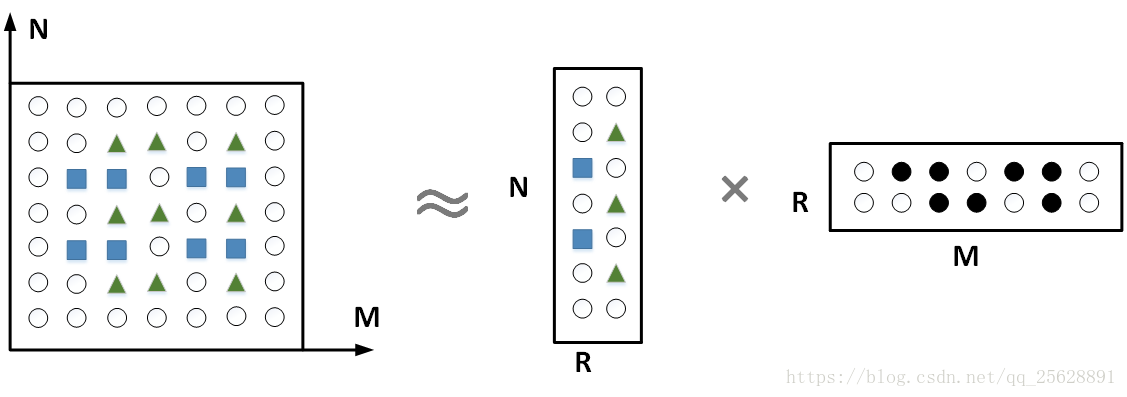
注：
W： 权重矩阵（字典矩阵）
H： 特征矩阵（扩展矩阵）
V： 原矩阵
为什么分解的矩阵式非负？
网上流传一种很有利的解释就是非负为了使数据有效，负数对于数据是无效的。个人认为取非负元素主要是运用于实际问题中。例如图像数据中不可能有负值的像素点，文本数据采用二进制表示…
- 非负性会引发稀疏
- 非负性会使计算过程进入部分分解
为什么要运用非负矩阵分解？
从上面的模型中，很容易发现：当N、M特别大时，原矩阵面积V远大于权重矩阵W和特征矩阵H的和，也就是n*m>>(n+m)*r。因此如果用W+H代替V来存储或读取，能很大程度上节约存储空间或大大提高读取速度。
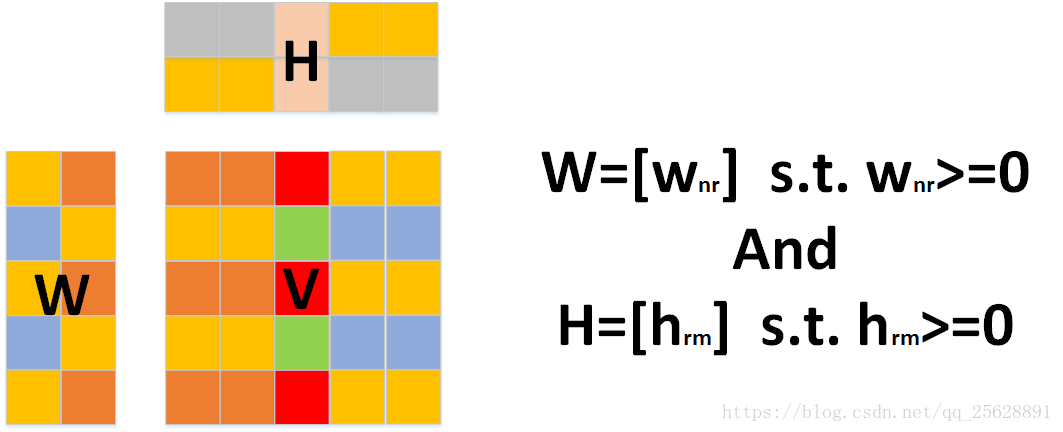
当然，讲到这里NMF好像很简单，只是对矩阵进行分解。不过仔细想想如果只是简单对矩阵进行分解早就被人提出来引用了，正是因为如何分解矩阵才能更好地对矩阵进行解析，也就是如何解NMF矩阵本身就是一个难题，因此还有很多问题值得我们一起去探讨的，接下来具体介绍下算法实现。
非负矩阵分解的算法和实现
NMF求解问题实际上是一个最优化问题，利用乘性迭代的方法求解和，非负矩阵分解是一个NP问题。NMF问题的目标函数有很多种，应用最广泛的就是欧几里得距离和KL散度。由于W与H的乘积是对V的近似估计，所以评价分解好坏的标准便是两者之间的差异。
两种损失函数的定义方式：
在 N M F 的 分 解 问 题 中 ， 假 设 噪 声 矩 阵 为 E ∈ R n ∗ m ， 那 么 有 E = V − W H 。 在NMF的分解问题中，假设噪声矩阵为E\in R^{n\ast m}，那么有E=V-WH。 在NMF的分解问题中，假设噪声矩阵为E∈Rn∗m，那么有E=V−WH。现在要找出合适的W和H使得||E||最小。
假设噪声服从不同的概率分布，通过最大似然函数会得到不同类型的目标函数。
a. 平方距离
噪声服从高斯分布
假设噪声服从高斯分布，也称作为平方距离。
平方距离定义：
∥
A
−
B
∥
2
=
∑
i
,
j
(
A
i
,
j
−
B
i
,
j
)
2
\left \| A-B \right \|^{2} = \sum_{i,j}\left ( A_{i,j}-B_{i,j} \right )^{2}
∥A−B∥2=i,j∑(Ai,j−Bi,j)2
step1：得到最大似然函数L(W,H)为
L
(
W
,
H
)
=
∏
i
,
j
1
2
π
σ
i
j
e
−
E
i
j
2
2
σ
i
j
=
∏
i
,
j
1
2
π
σ
i
j
e
−
[
V
i
j
−
(
W
H
)
i
j
]
2
2
σ
i
j
L(W,H) =\prod_{i,j}\frac{1}{\sqrt{2\pi} \sigma _{ij}}e^{-\frac{E_{ij}^{2}}{2 \sigma _{ij}}}=\prod_{i,j}\frac{1}{\sqrt{2\pi} \sigma _{ij}}e^{-\frac{[V_{ij}-(WH)_{ij}]^{2}}{2 \sigma _{ij}}}
L(W,H)=i,j∏2πσij1e−2σijEij2=i,j∏2πσij1e−2σij[Vij−(WH)ij]2
step2：两边取对数，得到对数似然函数lnL(W,H)
l
n
L
(
W
,
H
)
=
∑
i
,
j
(
l
n
1
2
π
σ
i
j
−
[
V
i
j
−
(
W
H
)
i
j
]
2
2
σ
i
j
)
=
∑
i
,
j
l
n
1
2
π
σ
i
j
−
1
σ
i
j
.
1
2
∑
i
,
j
[
V
i
j
−
(
W
H
)
i
j
]
2
lnL(W,H) =\sum_{i,j}(ln \frac{1}{\sqrt{2\pi}\sigma _{ij}}-\frac{[V_{ij}-(WH)_{ij}]^{2}}{2 \sigma _{ij}})=\sum_{i,j}ln \frac{1}{\sqrt{2\pi}\sigma _{ij}}- \frac{1}{ \sigma _{ij}}.\frac{1}{2}\sum_{i,j}[V_{ij}-(WH)_{ij}]^{2}
lnL(W,H)=i,j∑(ln2πσij1−2σij[Vij−(WH)ij]2)=i,j∑ln2πσij1−σij1.21i,j∑[Vij−(WH)ij]2
step3：假设各数据点噪声的标准差σ一样，那么接下来要使得对数似然函数lnL(W,H) 取值最大，只需要下面目标函数J(W,H)值最小
J
(
W
,
H
)
=
1
2
∑
i
,
j
[
V
i
j
−
(
W
H
)
i
j
]
2
J(W,H) = \frac{1}{2}\sum_{i,j}[V_{ij}-(WH)_{ij}]^{2}
J(W,H)=21i,j∑[Vij−(WH)ij]2
该函数是基于欧几里得距离的度量
(
W
H
)
i
j
=
∑
k
W
i
k
H
k
j
⇒
∂
(
W
H
)
i
j
∂
W
i
k
=
H
k
j
(
W
H
)
i
j
=
∑
k
W
i
k
H
k
j
⇒
∂
(
W
H
)
i
j
∂
H
k
j
=
W
i
k
(WH)_{ij} = \sum_{k}W_{ik}H_{kj}\Rightarrow \frac{\partial(WH)_{ij}}{\partial W_{ik}}=H_{kj}\\ (WH)_{ij} = \sum_{k}W_{ik}H_{kj}\Rightarrow \frac{\partial(WH)_{ij}}{\partial H_{kj}}=W_{ik}
(WH)ij=k∑WikHkj⇒∂Wik∂(WH)ij=Hkj(WH)ij=k∑WikHkj⇒∂Hkj∂(WH)ij=Wik
step4：目标函数J(W,H)求偏导
∂
J
(
W
,
H
)
∂
W
i
k
=
∑
i
,
j
[
H
k
j
(
V
i
j
−
(
W
H
)
i
j
)
]
=
∑
i
,
j
[
V
i
j
H
k
j
−
(
W
H
)
i
j
H
k
j
]
=
∑
i
,
j
[
V
i
j
H
j
k
T
−
(
W
H
)
i
j
H
j
k
T
]
=
(
V
H
T
)
i
k
−
(
W
H
H
T
)
i
k
\frac{\partial J(W,H)}{\partial W_{ik}}= \sum_{i,j}[H_{kj}(V_{ij}-(WH)_{ij})] =\sum_{i,j}[V_{ij}H_{kj}-(WH)_{ij}H_{kj}]\\ =\sum_{i,j}[V_{ij}H_{jk}^{T}-(WH)_{ij}H_{jk}^{T}] = (VH^{T})_{ik}-(WHH^{T})_{ik}
∂Wik∂J(W,H)=i,j∑[Hkj(Vij−(WH)ij)]=i,j∑[VijHkj−(WH)ijHkj]=i,j∑[VijHjkT−(WH)ijHjkT]=(VHT)ik−(WHHT)ik
同理
∂
J
(
W
,
H
)
∂
H
k
j
=
∑
i
,
j
[
W
i
k
(
V
i
j
−
(
W
H
)
i
j
)
]
=
∑
i
,
j
[
W
i
k
V
i
j
−
W
i
k
(
W
H
)
i
j
]
=
∑
i
,
j
[
W
k
i
T
V
i
j
−
W
k
i
T
(
W
H
)
i
j
]
=
(
W
T
V
)
k
j
−
(
W
T
W
H
)
k
j
\frac{\partial J(W,H)}{\partial H_{kj}}=\sum_{i,j}[W_{ik}(V_{ij}-(WH)_{ij})]= \sum_{i,j}[W_{ik}V_{ij}-W_{ik}(WH)_{ij}]\\ =\sum_{i,j}[W_{ki}^{T}V_{ij}-W_{ki}^{T}(WH)_{ij}] = (W^{T}V)_{kj}-(W^{T}WH)_{kj}
∂Hkj∂J(W,H)=i,j∑[Wik(Vij−(WH)ij)]=i,j∑[WikVij−Wik(WH)ij]=i,j∑[WkiTVij−WkiT(WH)ij]=(WTV)kj−(WTWH)kj
step5：使用梯度下降进行迭代
W
i
k
=
W
i
k
+
α
1
[
(
V
H
T
)
i
k
−
(
W
H
H
T
)
i
k
]
H
k
j
=
H
k
j
+
α
2
[
(
W
T
V
)
k
j
−
(
W
T
W
H
)
k
j
]
W_{ik}=W_{ik}+\alpha _{1}[(VH^{T})_{ik}-(WHH^{T})_{ik}]\\ H_{kj}=H_{kj}+\alpha _{2}[(W^{T}V)_{kj}-(W^{T}WH)_{kj}]
Wik=Wik+α1[(VHT)ik−(WHHT)ik]Hkj=Hkj+α2[(WTV)kj−(WTWH)kj]
step5：选取合适的α，得到最终迭代式
α
1
=
W
i
k
(
W
H
H
T
)
i
k
α
2
=
H
k
j
(
W
T
W
H
)
k
j
\alpha _{1} = \frac{W_{ik}}{(WHH^{T})_{ik}} \qquad \alpha _{2} = \frac{H_{kj}}{(W^{T}WH)_{kj}}
α1=(WHHT)ikWikα2=(WTWH)kjHkj
W
i
k
=
W
i
k
(
V
H
T
)
i
k
(
W
H
H
T
)
i
k
①
H
k
j
=
H
k
j
(
W
T
V
)
k
j
(
W
T
W
H
)
k
j
②
W_{ik}=W_{ik}\frac{(VH^{T})_{ik}}{(WHH^{T})_{ik}}① \qquad H_{kj}=H_{kj}\frac{(W^{T}V)_{kj}}{(W^{T}WH)_{kj}}②
Wik=Wik(WHHT)ik(VHT)ik①Hkj=Hkj(WTWH)kj(WTV)kj②
可看出这是乘性迭代规则，每一步都保证了结果为正数。
b. KL散度
噪声服从泊松分布
假设噪声服从泊松分布，也称作为KL散度。
step1：KL散度并不是那么的直观，下面画图来理解下。首先说明一点：KL散度是非对称的。
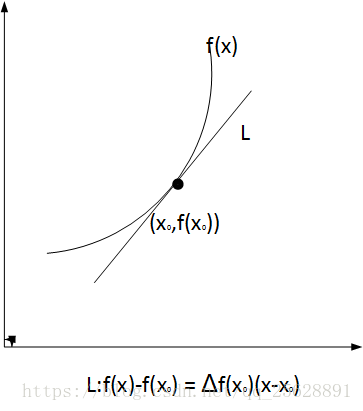
从图中很容易写出解的切线方程，其实如果接近，这就是一阶Taylor近似，写成更一般的形式：
f
(
y
)
≈
f
(
x
)
−
△
f
(
x
)
(
x
−
y
)
f(y)\approx f(x)-\triangle f(x)(x-y)
f(y)≈f(x)−△f(x)(x−y)
step2：推广开来这就是Bregman距离：
令
：
D
→
R
为
定
义
在
闭
合
凸
集
D
⊆
D
⊆
R
+
k
的
一
连
续
可
微
分
凸
函
数
。
−
−
与
函
数
对
应
的
两
个
向
量
x
,
y
∈
D
之
间
的
B
r
e
g
m
a
n
距
离
记
作
：
B
φ
(
x
∣
∣
y
)
=
φ
(
y
)
−
φ
(
x
)
+
⟨
△
φ
(
x
)
,
x
−
y
⟩
令：D\rightarrow R为定义在闭合凸集D\subseteq D\subseteq R_{+}^{k}的一连续可微分凸函数。\\ - - \\ 与函数对应的两个向量x,y\in D之间的Bregman距离记作：B_{\varphi}(x||y)=\varphi(y)-\varphi(x) + \langle \triangle \varphi(x),x-y\rangle \\
令：D→R为定义在闭合凸集D⊆D⊆R+k的一连续可微分凸函数。−−与函数对应的两个向量x,y∈D之间的Bregman距离记作：Bφ(x∣∣y)=φ(y)−φ(x)+⟨△φ(x),x−y⟩
step3：如果凸函数：
φ
(
x
)
=
∑
i
=
1
k
x
i
l
n
x
i
\varphi(x)=\sum_{i=1}^{k}x_{i}lnx_{i}
φ(x)=i=1∑kxilnxi
可以得到
B
φ
(
x
∣
∣
y
)
=
∑
i
=
1
k
[
y
i
l
n
x
i
−
x
i
l
n
x
i
+
(
l
n
x
i
+
1
)
(
x
i
−
y
i
)
]
=
∑
i
=
1
k
(
y
i
l
n
x
i
y
i
−
x
i
+
y
i
)
B_{\varphi}(x||y)=\sum_{i=1}^{k}[y_{i}lnx_{i}-x_{i}lnx_{i}+(lnx_{i}+1)(x_{i}-y_{i})] =\sum_{i=1}^{k}(y_{i}ln\frac{x_{i}}{y_{i}}-x_{i}+y_{i})
Bφ(x∣∣y)=i=1∑k[yilnxi−xilnxi+(lnxi+1)(xi−yi)]=i=1∑k(yilnyixi−xi+yi)
step4：所以通过KL散度定义的损失函数为：
D
(
A
∣
∣
B
)
=
∑
i
,
j
(
V
i
j
l
n
V
i
j
(
W
H
)
i
j
−
V
i
j
+
(
W
H
)
i
j
)
D(A||B) = \sum_{i,j} (V_{ij}ln\frac{V_{ij}}{(WH)_{ij}}-V_{ij}+(WH)_{ij})
D(A∣∣B)=i,j∑(Vijln(WH)ijVij−Vij+(WH)ij)
在KL散度的定义中，D(A∥B)⩾0，当且仅当A=B时取得等号。
此步证明可参考：https://blog.youkuaiyun.com/cumttzh/article/details/79790953
step5：目标函数J(W,H)求偏导
∂
J
(
W
,
H
)
∂
W
i
k
=
∑
i
,
j
(
H
k
j
−
V
i
j
H
k
j
(
W
H
)
i
j
)
=
∑
i
,
j
(
H
k
j
−
V
i
j
H
k
j
(
W
H
)
i
j
)
\frac{\partial J(W,H)}{\partial W_{ik}} = \sum_{i,j}(H_{kj}-V_{ij}\frac{H_{kj}}{(WH)_{ij}}) =\sum_{i,j}(H_{kj}-\frac{V_{ij}H_{kj}}{(WH)_{ij}})
∂Wik∂J(W,H)=i,j∑(Hkj−Vij(WH)ijHkj)=i,j∑(Hkj−(WH)ijVijHkj)
同理：
∂
J
(
W
,
H
)
∂
H
k
j
=
∑
i
,
j
(
W
i
k
−
V
i
j
W
i
k
(
W
H
)
i
j
)
=
∑
i
,
j
(
W
i
k
−
V
i
j
W
i
k
(
W
H
)
i
j
)
\frac{\partial J(W,H)}{\partial H_{kj}} = \sum_{i,j}(W_{ik}-V_{ij}\frac{W_{i k}}{(WH)_{ij}}) =\sum_{i,j}(W_{ik}-\frac{V_{ij}W_{ik}}{(WH)_{ij}})
∂Hkj∂J(W,H)=i,j∑(Wik−Vij(WH)ijWik)=i,j∑(Wik−(WH)ijVijWik)
step6：使用梯度下降进行迭代
W
i
k
=
W
i
k
+
α
1
∑
i
,
j
(
H
k
j
−
V
i
j
H
k
j
(
W
H
)
i
j
)
−
−
H
k
j
=
H
k
j
+
α
2
∑
i
,
j
(
W
i
k
−
V
i
j
W
i
k
(
W
H
)
i
j
)
W_{ik}=W_{ik}+\alpha _{1}\sum_{i,j}(H_{kj}-\frac{V_{ij}H_{kj}}{(WH)_{ij}})\\--\\ H_{kj}=H_{kj}+\alpha _{2}\sum_{i,j}(W_{ik}-\frac{V_{ij}W_{ik}}{(WH)_{ij}})
Wik=Wik+α1i,j∑(Hkj−(WH)ijVijHkj)−−Hkj=Hkj+α2i,j∑(Wik−(WH)ijVijWik)
step7：选取合适的α，得到最终迭代式
α
1
=
W
i
k
∑
i
,
j
(
W
H
)
i
j
V
i
j
H
k
j
α
2
=
H
k
j
∑
i
,
j
(
W
H
)
i
j
V
i
j
W
i
k
\alpha _{1} = W_{ik}\sum_{i,j}\frac{(WH)_{ij}}{V_{ij}H_{kj}} \qquad \alpha _{2} =H_{kj}\sum_{i,j}\frac{(WH)_{ij}}{V_{ij}W_{ik}}
α1=Wiki,j∑VijHkj(WH)ijα2=Hkji,j∑VijWik(WH)ij
W i k = W i k ∑ j H k j ∑ i , j ( W H ) i j V i j H k j ③ H k j = H k j α 2 ∑ i H i k ∑ i , j ( W H ) i j V i j W i k ④ W_{ik}=W_{ik}\sum_{j}H_{kj}\sum_{i,j}\frac{(WH)_{ij}}{V_{ij}H_{kj}}③ \qquad H_{kj}=H_{kj}\alpha _{2}\sum_{i}H_{ik}\sum_{i,j}\frac{(WH)_{ij}}{V_{ij}W_{ik}} ④ Wik=Wikj∑Hkji,j∑VijHkj(WH)ij③Hkj=Hkjα2i∑Hiki,j∑VijWik(WH)ij④
算法步骤
W
i
k
=
W
i
k
(
V
H
T
)
i
k
(
W
H
H
T
)
i
k
①
H
k
j
=
H
k
j
(
W
T
V
)
k
j
(
W
T
W
H
)
k
j
②
W_{ik}=W_{ik}\frac{(VH^{T})_{ik}}{(WHH^{T})_{ik}}① \qquad H_{kj}=H_{kj}\frac{(W^{T}V)_{kj}}{(W^{T}WH)_{kj}}②
Wik=Wik(WHHT)ik(VHT)ik①Hkj=Hkj(WTWH)kj(WTV)kj②
W
i
k
=
W
i
k
∑
j
H
k
j
∑
i
,
j
(
W
H
)
i
j
V
i
j
H
k
j
③
H
k
j
=
H
k
j
α
2
∑
i
H
i
k
∑
i
,
j
(
W
H
)
i
j
V
i
j
W
i
k
④
W_{ik}=W_{ik}\sum_{j}H_{kj}\sum_{i,j}\frac{(WH)_{ij}}{V_{ij}H_{kj}}③ \qquad H_{kj}=H_{kj}\alpha _{2}\sum_{i}H_{ik}\sum_{i,j}\frac{(WH)_{ij}}{V_{ij}W_{ik}} ④
Wik=Wikj∑Hkji,j∑VijHkj(WH)ij③Hkj=Hkjα2i∑Hiki,j∑VijWik(WH)ij④
a. 平方距离
1）随机生成一个W矩阵；
2）固定H，按照公式①迭代更新W直到收敛（W不变或变化很小）
3）固定W，按照公式②迭代更新H直到收敛（H不变或变化很小）
4）重复2）、3）步骤直到对应的损失函数不变或变化很小
b. KL散度
1）随机生成一个W矩阵；
2）固定H，按照公式③迭代更新W直到收敛（W不变或变化很小）
3）固定W，按照公式④迭代更新H直到收敛（H不变或变化很小）
4）重复2）、3）步骤直到对应的损失函数不变或变化很小
非负矩阵分解的伪代码
输入参数：Ｘ，Ｒ，MATRIX
============> Ｘ为被分解的矩阵
============> Ｒ为降阶后W的秩
============> MATRIX为迭代次数
输出参数：W，Ｈ
１）：初始化矩阵W，Ｈ为非负数，同时对W的每一列数据归一化
２）：for i=1:MAXITER
a：更新矩阵H的一行元素：H(i,k)=H(i,j)×(W’×X)(i,j)/(W’×W×H)(k,j)
b：更新矩阵W的一列元素：W(k,j)=W(k,j)×(X×H’)(k,j)/(W×H×H’)(i,k);
c: 重新对B进行列归一化
3）end
扫一扫
1402
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
