排序算法学习--直接插入排序--希尔排序@python

插入排序和希尔排序的python代码如下：

def DirectInsertionSort(datalist):
    n = len(datalist)
    for i in range(1,n):
            for j in range(i,0,-1):
                if datalist[j] < datalist[j-1]:
                    datalist[j], datalist[j-1] = datalist[j-1], datalist[j]
    return datalist  

def shellSort(datalist):
    n = len(datalist)
    increment = n
    while(True):
        increment = int(increment/3) + 1
        for i in range(increment,n):      
            # 从第个元素开始，依次和前面已经排好序的i-increment个元素比较。小于则交换
            for j in range(i,increment-1,-increment):
                if datalist[j] < datalist[j-increment]:
                    datalist[j], datalist[j-increment] = datalist[j-increment], datalist[j]
        if increment <= 1 : break
    return datalist    

datalist = [9,1,5,8,3,7,4,6,2]
sortedlist = DirectInsertionSort(datalist)

插入排序的动画演示如下：

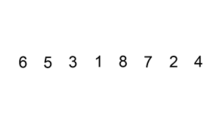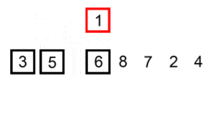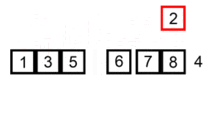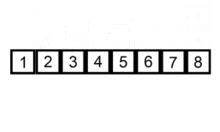
以打扑克牌为例，假如手中已有的若干张牌从左至右按照从小到大的顺序排列，当新摸到一张牌时，和手中的牌从左到右依次进行比较，并插入到合适的位置，此时手中的扑克牌仍然保持从左至右按照从小到大的顺序排列。

具体步骤如下：

1. 从第一个元素开始，认为该元素已排序；
2. 取出下一个元素，并从后往前依次与前面已排好序的元素序列进行比较。
3. 如果该元素大于前面一位的有序元素，则重复步骤2。
4. 如果该元素 < 前面某元素，则交换位置，直到遍历完前面的有序元素序列。
5. 重复步骤2,3,4，直至所有元素排好序。

插入排序对于近似有序的序列来说，可以达到线性排序的效率。但插入排序效率仍然比较低，因为一次只能将元素向前移动一位。当一个长度为N的序列，最小的元素如果恰巧在末尾，那么使用插入排序需要一步一步向前移动和比较，则需要N-1次比较和交换。

希尔排序

希尔排序也称之为递减增量排序。

希尔排序是在插入排序的基础上改进的。这里插入排序的步长为1，每一次递减1，希尔排序的步长为increment，然后每一次和前面的-increment位置上的元素进行比较。算法中首先获取小于n/3+1 的最大的步长，然后步长递减至为1，此时就是一般的插入排序。

希尔排序通过将待比较的元素划分为几个区域来提升插入排序的效率。这样可以让元素一次性的朝最终位置迈进一大步，然后算法再取越来越小的步长进行排序，直至步长为1时进行一般的插入排序，此时因为整个序列已经近似有序，所以效率仍然很高。

注意，增量序列的最后一个增量值必须等于1。

如下图所示，

• 当对图中数组进行排序时，首先步长为4，此时数组分为了LMPT，EHSS，ELOX，AELR共4个序列，分别对这几个独立的序列进行插入排序。
• 减小步长，继续排序。
• 步长为1时即为一般的插入排序。

希尔排序的增量选择很重要，但是应该怎样选取增量最好，仍然是一个数学难题，迄今为止没人找到一种最好的增量序列。

算法	最好	最差
冒泡排序法	n	n2
简单选择排序法	n2	n2
插入排序	n	n2
希尔排序	n	依赖增量递减序列，目前最好的是 nlog2n。