强化学习（RLAI）读书笔记第十一章 Off-policy Methods with Approximation

最新推荐文章于 2025-03-05 14:47:42 发布

无所知

最新推荐文章于 2025-03-05 14:47:42 发布

阅读量2.6k

点赞数 2

分类专栏：强化学习文章标签： RLAI

本文链接：https://blog.youkuaiyun.com/qq_25037903/article/details/82713736

版权

本文详细探讨了强化学习中off-policy方法在函数近似下的拓展和挑战，包括半梯度方法的收敛问题、更新分布差异带来的困难。重点介绍了Semi-gradient Methods、Gradient-TD和Emphatic-TD算法，强调了 Deadly Triad（函数近似、自举、off-policy训练）组合的不稳定性，并提出减少方差的策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本书第五章就已经讲解过分别使用on-policy和off-policy方法来解决GPI框架里固有的explore和exploit的矛盾。前两章已经讲了on-policy情形下对于函数近似的拓展，本章继续讲解off-policy下对函数近似的拓展，但是这个拓展比on-policy时更难更不同。在第六第七章中讲到的off-policy方法可以拓展到函数近似的情况下，但是这些方法在半梯度法下不能像在on-policy下一样良好地收敛。这一章我们将会讨论收敛的问题并且更进一步观察线性函数近似的理论。介绍一个可学习性（learnability）的概念以及讨论能够在off-policy下提供更强收敛性的新算法。

函数近似下的off-policy算法主要有两个难点。第一个在网格形式下就有，另一个是源自函数近似方法。第一个难点就是对于更新目标的修正，另一个就是解决更新的分布的问题。第五章和第七章的方法以及可以解决第一个修正更新目标的问题，尽管这些方法会带来很大的方差但是在网格下和函数近似下都是必不可少的。这些方法到函数近似的拓展就可以解决第一个难点。

第二个在函数近似off-policy算法中的难点需要额外的方法来解决，因为off-policy下产生的更新分布不是根据on-policy分布。而on-policy分布对于半梯度方法的稳定性很重要。大致两种方法可以解决这个问题。第一种是再次使用importance sampling的方法将更新的分布变形至on-policy的分布，这样就能够保证（线性逼近下）半梯度法的收敛性。另一种方法是使用真正的不需要依赖特定分布就保证收敛的梯度下降法。我们这两种方法都提供了。

11.1 Semi-gradient Methods

先进行描述如何把先前表格型off-policy情形下的算法改编为半梯度法。这些方法解决了off-policy下的第一个难题也就是更新目标的修正。这些方法在某些情形下会发散，但是依然能够成功使用。首先记住这些方法能够在表格情形下保证收敛至渐进无偏的值，而表格情形是函数逼近的一种特殊情况。所以依然有可能将这些算法与某些特征选择方法结合来达到类似的收敛效果。

为了将第七章中很多off-policy算法改编为半梯度的形式，我们只需要简单的把对于一个值函数列表的更新改编为对近似函数和其梯度的使用以及对参数 $w_{t}$ 的更新。每一步中的importance sampling ratio为：

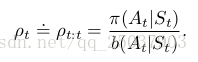
比如一步状态值函数算法也就是半梯度off-policy TD(0)算法的更新和on-policy形式的更新没有什么不同，除了增加了采样比重：

其中误差 $\delta_{t}$ 可以分为episodic和continuing两种情形：

而对于使用动作值函数的情况，一步算法是半梯度Expected Sarsa算法：

这个算法没有使用importance sampling。对于表格形式下这很好理解，因为只学习了一个动作 $A_{t}$ 的值函数，而不需要考虑其它动作。使用函数逼近这个概念就不那么清晰，因为可能有不同的状态动作对会改变当前值函数的估计，而这些对需要被不同对待。

在这些算法的多步形式中，状态值函数和动作值函数算法都需要importance sampling。比如n步半梯度expected Sarsa算法：

其中反馈也有episodic和continuing两种形式（感觉此处有误，个人感觉这似乎不是expected Sarsa而是普通Sarsa）：

这里写的不太规范因为最后t+n可能大于T。

以及第七章还有一种不需要importance sampling的算法：n步tree-backup算法。它的半梯度法如下：

11.2 Examples of Off-policy Divergence

这节开始讨论第二个off-policy使用函数近似下的难题，也就是更新的分布不同于on-policy的分布。描述了一些指导性的反例来说明半梯度法和其它一些算法的不稳定性和发散性。

例子描述略过。结论是，参数更新的稳定性和步长参数无关，只需要步长是大于0。更大或者更小的步长只会影响参数w走向无穷大的速度而不是它是否会发散。

例子中的关键部分就是这个状态的转移一直重复的发生而没有在其它转移上进行过更新。这是一种off-policy下可能的情况，因为行为策略可能在别的转以上都选择了目标策略不会选择的动作。这个简单的例子说明了off-policy发散的原因，但是它并不完全，这只是一个MDP过程的片段。还有个例子叫做Baird's counterexample的使用状态值函数V的例子。这个例子说明了只要是bootstrapping和半梯度法函数近似在不遵循on-policy分布的时候进行结合，那么参数都不会收敛。

对于Q-learning来说也有一个表示其发散的例子。而Q-learning如果收敛那么他就是最能够保证收敛的control算法。因此进行了一些修补，只要是使用和目标策略足够相近的策略就可以保证参数收敛比如动作策略是目标策略的 $\epsilon$ -greedy策略。目前还没有发现在这种情况下Q-learning会发散。