DataWhale集训-6.实战DP_pd的choicelistfieldactivity-优快云博客

本文深入解析了0-1背包问题的动态规划解决方案，阐述了贪心策略为何在此类问题中失效，并通过实例展示了动态规划的填表过程。同时，文章还介绍了LeetCode上的Palindrome Partitioning II题目，提供了使用动态规划解决该问题的思路与代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【任务6，实战DP】

实战DP：完成0-1背包问题实现(自我实现)及Leetcode上Palindrome Partitioning II(132)。

0-1背包问题：

0-1背包问题：有一个贼在偷窃一家商店时，发现有n件物品，第i件物品价值vi元，重wi磅，此处vi与wi都是整数。他希望带走的东西越值钱越好，但他的背包中至多只能装下W磅的东西，W为一整数。应该带走哪几样东西？这个问题之所以称为0-1背包，是因为每件物品或被带走；或被留下；小偷不能只带走某个物品的一部分或带走同一物品两次。

在分数（部分）背包问题（fractional knapsack problem)中，场景与上面问题一样，但是窃贼可以带走物品的一部分，而不必做出0-1的二分选择。可以把0-1背包问题的一件物品想象成一个金锭，而部分问题中的一件物品则更像金沙。

两种背包问题都具有最优子结构性质。对0-1背包问题，考虑重量不超过W而价值最高的装包方案。如果我们将商品j从此方案中删除，则剩余商品必须是重量不超过W-wj的价值最高的方案（小偷只能从不包括商品j的n-1个商品中选择拿走哪些）。

　　虽然两个问题相似，但我们用贪心策略可以求解背包问题，而不能求解0-1背包问题，为了求解部分数背包问题，我们首先计算每个商品的每磅价值vi/wi。遵循贪心策略，小偷首先尽量多地拿走每磅价值最高的商品，如果该商品已全部拿走而背包未装满，他继续尽量多地拿走每磅价值第二高的商品，依次类推，直到达到重量上限W。因此，通过将商品按每磅价值排序，贪心算法的时间运行时间是O(nlgn)。

　　为了说明贪心这一贪心策略对0-1背包问题无效，考虑下图所示的问题实例。此例包含3个商品和一个能容纳50磅重量的背包。商品1重10磅，价值60美元。商品2重20磅，价值100美元。商品3重30磅，价值120美元。因此，商品1的每磅价值为6美元，高于商品2的每磅价值5美元和商品3的每磅价值4美元。因此，上述贪心策略会首先拿走商品1。但是，最优解应该是商品2和商品3，而留下商品1。拿走商品1的两种方案都是次优的。

　　但是，对于分数背包问题，上述贪心策略首先拿走商品1，是可以生成最优解的。拿走商品1的策略对0-1背包问题无效是因为小偷无法装满背包，空闲空间降低了方案的有效每磅价值。在0-1背包问题中，当我们考虑是否将一个商品装入背包时，必须比较包含此商品的子问题的解与不包含它的子问题的解，然后才能做出选择。这会导致大量的重叠子问题——动态规划的标识。

例子：0-1背包问题。总共有三件物品，背包可容纳5磅的东西，物品1重1磅，价值60元。物品2重2磅，价值100元，物品3重3磅，价值120元。怎么才能最大化背包所装物品的价值。

解答：我们可以得出物品一每磅价值60元，大于物品二的每磅50元和物品3的每磅40元。如果按照贪心算法的话就要取物品1。然而最优解应该取的是物品2和3，留下了1.在0-1背包问题中不应取物品1的原因在于这样无法将背包填满，空余的空间就降低了货物的有效每磅价值。我们可以利用动态规划来解0-1背包问题。

假设c[i]表示第i件物品的重量，w[i]表示第i件物品的价值，f[i][j]表示背包容量为j,可选物品为物品1~i时，背包能获得的最大价值。用动态规划求解即先求出背包容量较小时能获得的最大价值，然后根据背包容量较小时的结果求出背包容量较大时的结果，也就是一个递推的填表过程。当没有可选物品时，背包能获得的最大价值为0。即表格可初始化为

填表过程（即状态转移方程）是：

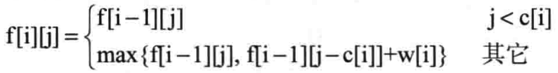
"j<c[i]"表示第i件物品的重量大于当前背包的容量j，此时显然不放第i件物品。下面解释上述方程在“其它“情况下的意义：”将前i件物品放入容量为j背包中“这个问题，如果只考虑第i件物品放或者不放，那么就可以转化为只涉及前i-1件物品的问题，即：

1. 如果不放第i件物品，则问题转化为只涉及”前i-1件物品放入容量为j的背包中“

2. 如果放第i件物品，则问题转化为”前i-1件物品放入剩下的容量为j-c[i]的背包中“，此时能获得的最大价值就是f[i-1][j-c[i]]再加上通过放入第i件物品获得的价值获得的价值w[i]。则在”其他“情况下，f[i][j]就是1、2中最大的那个值。

显然，可以从左下角利用状态转移方程依次逐行填表，得到f[3][5]（表示可选物品为1、2、3，且背包容量为5时，能获得的最大价值），可见动态规划的确即为一个递推的过程。填表后如下表所示：

实现代码：

int N = 3, V = 5;    //N是物品数量，V是背包容量
int c[4] = {0,1,2,3};
int w[4] = {0.60.100.120};
for (i = 0; i <= V; i++) { //逐行填表，i表示当前可选物品数，j表示当前背包的容量
    f[i][0] = 0;
    for (j = 1; j <= V; j++) {
        if (j < c[i]) {
            f[i][j] = f[i-1][j];
        } else {
            f[i][j] = max(f[i-1][j], f[i-1][j-c[i]] + w[i]);
        }
    }
}

132. Palindrome Partitioning II

Given a string s, partition s such that every substring of the partition is a palindrome.

Return the minimum cuts needed for a palindrome partitioning of s.

Example:

思想：

以一个字符为中心，向两边扩展，如果是回文串就更新最小分割次数，但是回文串可能是偶数个，也可能是奇数个。所以需要考虑以当前字符为中心，或者以当前字符以及当前字符下一个字符共同为中心，进行两边扩展。如果为回文串，则更新最小分割数，注意这里不是个更新中心点的位置，而是回文串末尾的位置。
假设vector<int> nums(len+1,0)表示字符串的位置i（索引从1开始）的最小切割次数，j到i区间子串为回文串，那么nums[i+1]=min(nums[i+1],nums[j]+1)
例如 s=adcbc
以b为中心扩展的时候可以得到cbc为回文串，那么此时切割数最小就是ab最小的切割数+1，即nums[5]=min(nums[5],nums[2]+1)

完整代码：

class Solution {
public:
    int minCut(string s) {
        if(s.size()==0) return 0;
        int len=s.size();
        vector<int> nums(len+1,0);
        for(int i=0;i<=len;i++) nums[i]=i-1;
        for(int i=1;i<=len;i++){
            for(int j=0;j<i&&i+j<=len&&s[i-j-1]==s[i+j-1];j++){
                nums[i+j]=min(nums[i+j],nums[i-j-1]+1);
            }
            for(int j=0;i-j>0&&i+j+1<=len&&s[i-1]==s[i]&&s[i-j-1]==s[i+j];j++){
                nums[i+j+1]=min(nums[i+j+1],nums[i-j-1]+1);
            }
        }
        return nums[len];
    }
};

参考资料：

1.【算法问题】0-1背包问题

2. [C++] LeetCode 132. 分割回文串 II